I уровень

1.1. Даны векторы Найдите координаты вектора:

1) 2)

3) 4)

1.2. Даны векторы Определите, при каком значениивекторыиколлинеарны.

1.3. Вектор образует с ортомуголα, с ортом угол. Вычислите координаты вектора на плоскости, если:

1) 2)

3) 4)

5) 6)

7) 8)

1.4. Заданы векторы Вы­числите:

1) 2) орты векторов

3) 4) координаты вектора

1.5. Вычислите скалярное произведение векторов, заданных своими координатами:

1) 2)

1.6. Найдите угол между векторами:

1) 2)

1.7. Вычислите работу, производимую силой при перемещении ее точки приложения из начала в конец вектора

II уровень

2.1. Известно, что A(2, –7), B(4, 1). Найдите:

1) координаты вектора 2)3) орт вектора

2.2. Даны векторы Определите, при каком значении коэффициентаk векторы коллинеарны:

1) и2)и

3) и.

2.3. Известно, что вектор является суммой векторовНайдитеm и n.

2.4. Отрезок с концами в точках А(3, –2) и В(6, 4) разделен на три равные части. Найдите координаты точек деления.

2.5. Вычислите скалярное произведение векторов и если:

1)

2)

2.6. Найдите угол между векторами иеслиА(2, 1), В(–1, 3) и С(4, –2).

III уровень

3.1. Сила разложена по двум перпендикулярным направлениям, одно из которых задано векторомНайдите направляющую силы в направлении этого вектора.

3.2. Подберите ненулевые числа α, β, γ так, чтобы

где

3.3. Даны три вершины А(3, –4), В(–5, 3) и С(1, 2) параллелограмма ABCD. Найдите его четвертую вершину D.

3.4. Даны вершины треугольника А(3, –1), В(4, 2) и С(–4, 0). Найдите длину медианы, проведенной из вершины А.

3.5. Даны вершины А(1, –1), В(2, 1) и С(–5, 2) треугольника АВС. Вычислите длину биссектрисы его внутреннего угла при вершине А.

3.6. Треугольник АВС задан координатами своих вершин: А(3, –2), В(3, 1) и С(4, 0). Вычислите расстояние от начала координат до точки пересечения медиан этого треугольника.

3.7. В вершинах треугольника А(1, –1), В(0, 4) и С(2, –1) сосредоточены массы соответственно 1, 2, 3. Найдите координаты центра масс этой системы.

З а м е ч а н и е. Для пары масс m₁ и m₂, сосредоточенных в точках А и В, центр находится в точке, делящей отрезок АВ в отношении где l₁ и l₂ – расстояния от точек с соответствующими массами до их центра.

3.8. Даны векторы Найдите вектор лежащий с векторамиив одной плоскости, перпендикулярный векторуравный ему по длине и образующий с векторомтупой угол.

3.9. Представьте ненулевой вектор в виде линейной комбинации векторови

8.3. Полярная система координат. Способы задания

кривой на плоскости

Выделим на плоскости произвольную точку О – полюс – и проведем числовой луч ОР – полярную ось. Расстояние от полюса до произвольной точки М обозначим ρ, а величину угла, на который нужно повернуть ОР, чтобы совместить с ОМ, обозначим через φ. Будем считать φ положительным, если поворот совершается против часовой стрелки, и отрицательным – в противном случае.

Величины ρ и φ называются полярными координатами точки М: ρ – полярный радиус, φ – полярный угол. Принято считать, что илиа полюс имеет нулевые полярные координаты.

Если заданы одновременно прямоугольная система координат xOy и полярная с полярной осью Ox, то можно установить связь между прямоугольными (x, y) и полярными (ρ, φ) координатами точки М на плоскости с помощью следующих формул:

(8.9)

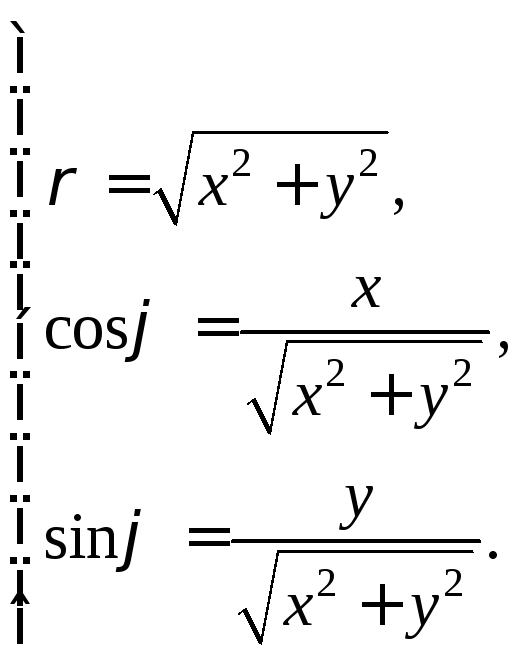(8.10)

Можно рассматривать уравнения кривых в полярных координатах: ρ = ρ(φ) или Ф(ρ, φ) = 0.

Пример 1. Найти полярные координаты точек

Решение. Точка лежит в I четверти прямоугольной системы координат. Значит, полярный угол φ удовлетворяет условию 0 < φ < π/2, причем согласно первой формуле системы (8.10):

Следовательно, что приводит кИтак,

Точка является внутренней точкойIII четверти прямоугольной системы координат, следовательно, (или). Найдем полярный радиус (используем формулы (8.10)):

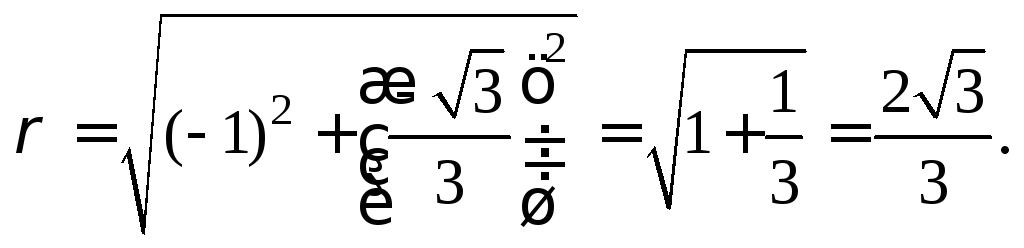
Тогда 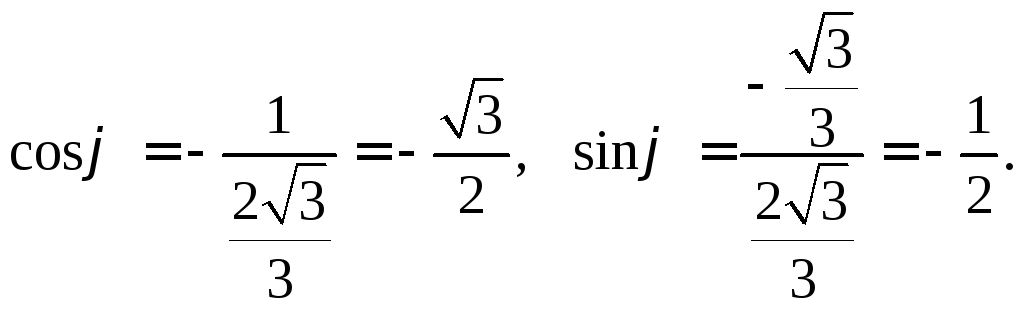Значит,илиТаким образом, точкуB в полярной системе координат можно задать как Bили

Рассмотрим точку С. Учитывая, что а значит,определяем, что точкаС лежит во II четверти прямоугольной системы координат. Ее полярный радиус, согласно формулам (8.10), есть

Для нахождения полярного угла φ поступим следующим образом. Найдем затем, воспользовавшись тем, что наименьший положительный период функцииy = tgx равен π, а угол φ удовлетворяет соотношению получим:

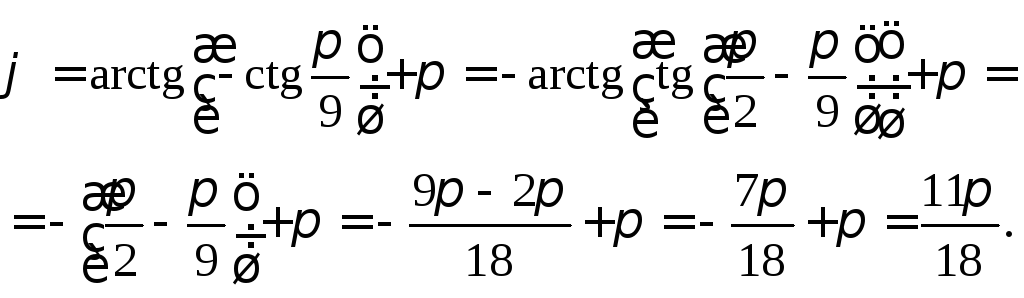
Значит,

За м е ч а н и е. При использовании формулыпри нахождении полярного угла целесообразно изображать эти точки на чертеже (рис. 8.10).

Рис. 8.10

Пример 2. Зная полярные координаты точек ,найти их прямоугольные координаты.

Решение. Используя формулы (8.9), находим прямоугольные координаты заданных точек:

Следовательно,

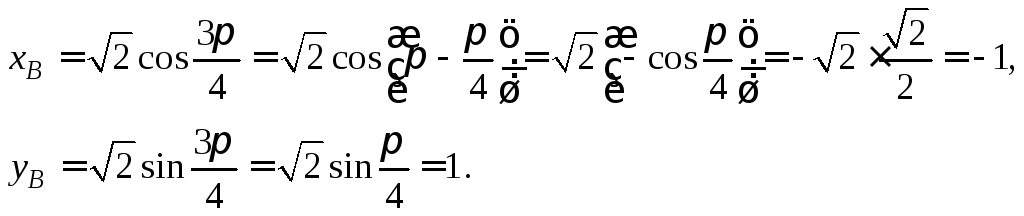
Следовательно, B(–1, 1).

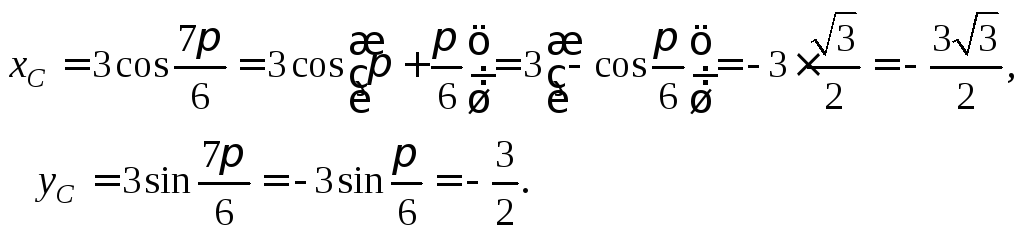
Следовательно,

Пример 3. Зная полярные координаты точки  = 10, найти ее прямоугольные координаты, если полюс находится в точкеА(2, 3), а полярная ось параллельна оси Ox.

Решение. Рассмотрим прямоугольную систему координат xOy, удовлетворяющую условию задачи (рис. 8.11). Тогда точка в этой системе координат определена какМ(x_M, y_M).

Очевидно, что

Таким образом, в заданной прямоугольной системе координат точка М определена как

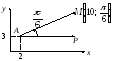
Рис. 8.11

Пример 4. Составить параметрические уравнения окружности x² + y² = 1, приняв за параметр угол между осью Ox и радиус-вектором гдеО – центр окружности, М – ее точка.

Решение. Пусть точка М имеет прямоугольные координаты Тогда, по определению тригонометрических функций, где Таким образом, получили параметрические уравнения окружности.

Пример 5. Найти уравнение фигуры на плоскости в прямоугольных координатах, если она имеет следующее уравнение в полярной системе координат:

1)  = 4; 2) 3) = 2cosφ.

Решение. Для решения примеров будем использовать формулы (8.10).

1) Поскольку Возводим в квадрат и получаем– уравнение окружности с центром в точке (0, 0) и радиусомr = 4.

2) Уравнение означает, что причем точка с координатами (x, y) лежит в I четверти. Значит, илиПолучим уравнение луча с началом в точке (0, 0).

3) Заданное уравнение запишем в видеПолучилиВыделяем полный квадрат и приходим к уравнениюкоторое есть уравнение окружности с центром в точке (1, 0) и радиусомr = 1.

Задания