I уровень

1.1. Определите, сколько различных векторов задают упорядоченные пары точек, составленные из вершин:

1) треугольника; 2) параллелограмма.

1.2. В плоскости треугольника ABC взята точка О. Отложите от нее вектор:

1) 2)3)

1.3. По заданным векторам ипостройте их линейные комбинации:

1) 2)3)4)

1.4. Вычислите скалярное произведение векторов иесли:

1) 2)

3) 4)

1.5. Зная, что вычислите:

1) 2)3)

4) 5)6)

1.6. К точке О приложены две силы и для которыха угол между направлениями этих сил равен 120. Найдите величину равнодействующей этих сил.

1.7. В треугольнике ABC задается: ТочкиM, N, P являются серединами сторон BC, AC и AB соответственно. Выразите векторы через векторы

II уровень

2.1. Определите, на какое число нужно умножить ненулевой вектор чтобы получить векторудовлетворяющий следующим условиям:

1) 2)

3) где4)

2.2. Определите, каким условиям должны удовлетворять ненулевые векторы ичтобы:

1) 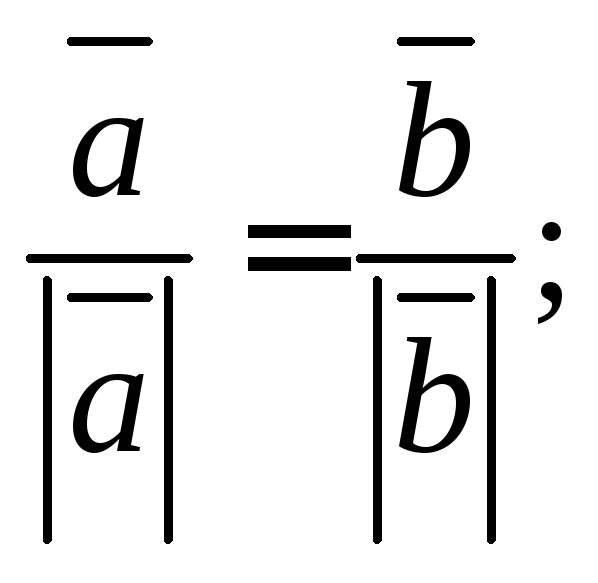2)

2.3. Найдите иесли векторыиперпендикулярны, причем

2.4. Вычислите если

2.5. Вычислите если

2.6. Найдите длину вектора если (все векторы лежат в одной плоскости).

2.7. Вычислите длины диагоналей параллелограмма, построенного на векторах игдеи– единичные векторы, угол между которыми равен 60.

2.8. Найдите еслигде

2.9. Определите, какой угол образуют единичные векторы иесли известно, что векторыивзаимно перпендикулярны.

2.10. В параллелограмме ABCD длины векторов равны соответственно 2, 3, 4. Найдите скалярное произведение векторови

2.11. Найдите угол между векторами иесли

III уровень

3.1. Точки K, L являются серединами сторон AD и AB параллелограмма ABCD. Полагая выразите векторыичерез векторыи.

3.2. В треугольнике ABC проведена биссектриса AD угла A. Найдите разложение вектора по векторами

3.3. В параллелограмме ABCD точки M и N являются серединами сторон AD и CD соответственно. Выразите вектор черезеслиО – точка пересечения отрезков AN и BM.

3.4. Катеты AB и AC прямоугольного треугольника ABC соответственно равны 6 и 8. Найдите косинус угла между векторами иесли известно, чтоAM и BN – биссектрисы углов А и В заданного треугольника.

3.5. Площадь равнобедренного треугольника равна а угол при вершинеА – 120. Найдите скалярное произведение векторов иесли известно, чтоK и L – середины соответственно сторон BC и AC треугольника ABC.

3.6. Вычислите если

8.2. Операции над векторами в координатной форме

Прямоугольная декартова система координат Oxy на плоскости задается совокупностью точки О (начало системы координат) и пары перпендикулярных единичных векторов ,При этом ось Ox, направление которой совпадает с направлением вектора называетсяосью абсцисс. Ось Оy, совпадающая по направлению с вектором –осью ординат. Вся плоскость называется координатной плоскостью xOy. За масштабную единицу выбирают длину

Координатами точки М являются перпендикулярные проекции точки М на координатные оси Ox и Oy, взятые с соответствующим знаком. Таким образом, точке М на плоскости соответствует упорядоченная пара (x, y) действительных чисел x и y. Пишут: M(x, y).

Каждой точке М на плоскости соответствует единственный радиус-вектор который имеет те же координаты, что и точкаМ. Пишут: Векторможет быть представлен также в виде линейной комбинации векторов

Если на плоскости заданы точки A(x₁, y₁), B(x₂, y₂), то

длина

(8.1)

Пусть тогда его единичный вектор (орт) есть

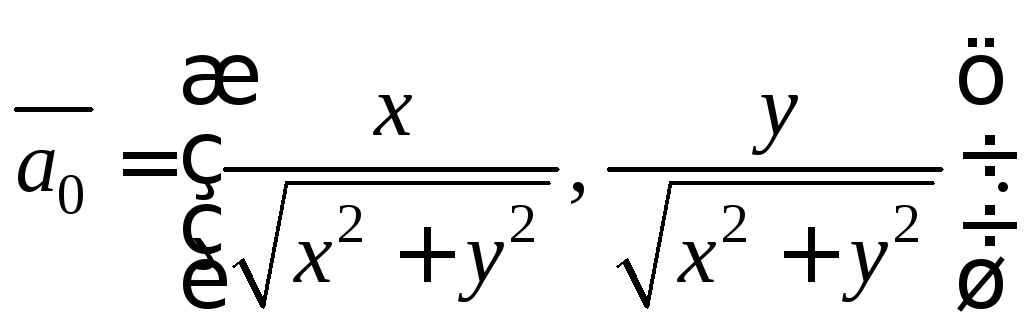(8.2)

При этом координаты орта задают направление вектораи называютсянаправляющими косинусами. Если  и  – углы между вектором и базисными векторамиисоответственно, то

(8.3)

Если то верны формулы:

(8.4)

(8.5)

(8.6)

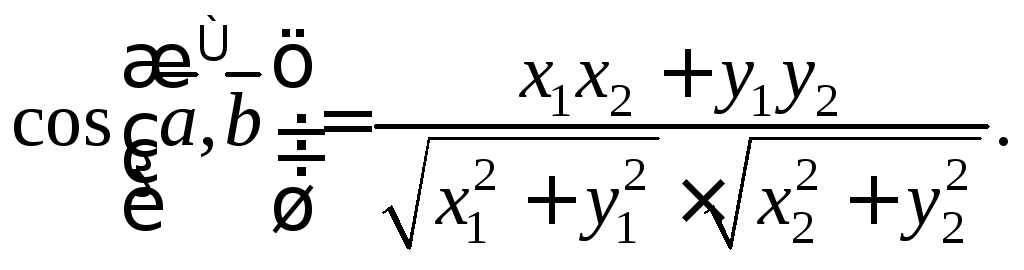(8.7)

Для коллинеарных векторов справедливо:

Координаты точки C(x_c, y_c), делящей отрезок AB в отношении λ > 0, находят по формулам:

(8.8)

Пример 1. Вектор образует с векторомуголс векторомуголНайти координаты векторана плоскости, если

Решение. Орт векторана плоскостиxOy имеет координаты Используя формулы (8.2) и (8.3), получаемТак както

Пример 2. Найти координаты векторов, определяемых диагоналями параллелограмма, построенного на векторах

Решение. Известно, что сумма и разность векторов иопределяют диагонали параллелограмма, построенного на них. Следовательно,Тогда

и, значит,

Аналогично находим

Пример 3. Координаты левого конца отрезка AB и его середины M соответственно равны A(–1, –5) и M(3, –2). Найти координаты точки В.

Решение. Пусть В(x_B, y_B). Середина отрезка делит его длину в отношении 1:1, т. е. λ = 1. Значит, из формул (8.8) имеем:

Выразив иполучаем:

Приходим к ответу: В(7, 1).

Пример 4. Даны векторы Вычислить:

1) 2)3)4)

Решение. 1) Используя формулу (8.6), имеем:

2) Согласно формулам (8.4) и (8.5), получаем:

Тогда на основании формулы (8.10) вычисляем:

Получить тот же результат можно и несколько по-другому. Используем свойства скалярного произведения, а затем формулы (8.1) и (8.6):

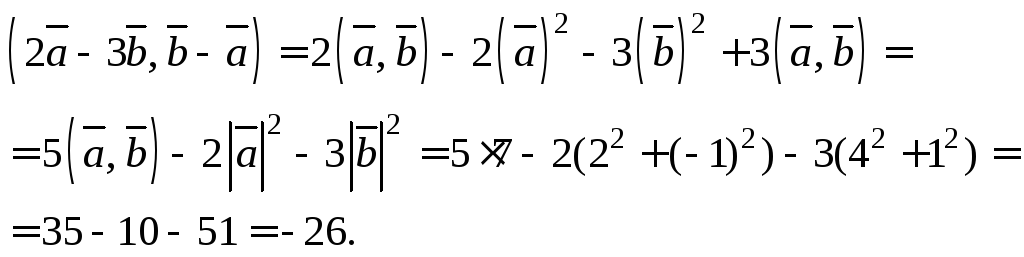
3) Найдем координаты вектора используя формулы (8.4) и (8.5):

Следовательно, по формуле длины вектора (8.1) получаем:

В качестве второго способа решения примера можно использовать следующий. Поскольку то

Находим:

4) Используем формулу (8.7) и получаем:

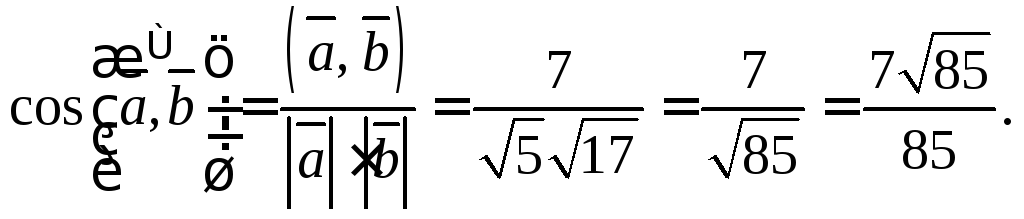
Пример 5. Даны векторы Найти косинус угла между векторамиидля которых

Решение. Выразим из первого заданного соотношения:Тогда, подставив во второе соотношение, получимоткуда

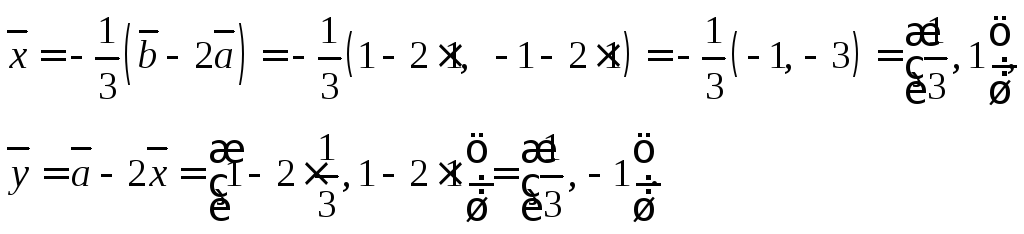
Следовательно, на основании формулы (8.7) получаем:

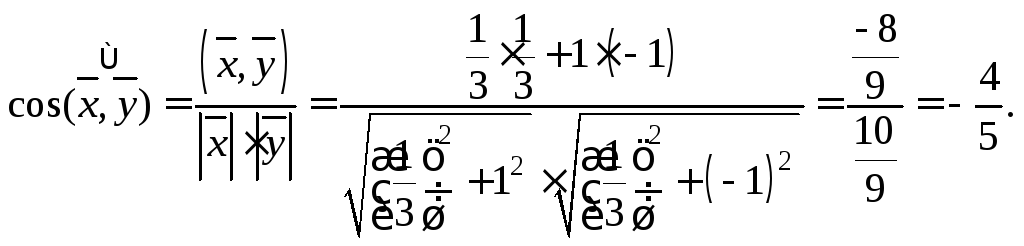
Пример 6. Пусть векторы получены из векторовповоротом относительно точкиО на угол (рис. 8.9). Представить произвольный векторв виде линейной комбинации векторовесли

Рис. 8.9

Решение. Зафиксируем прямоугольную систему координат с единичными векторамиВ этой системе координат определим направляющие косинусы векторов

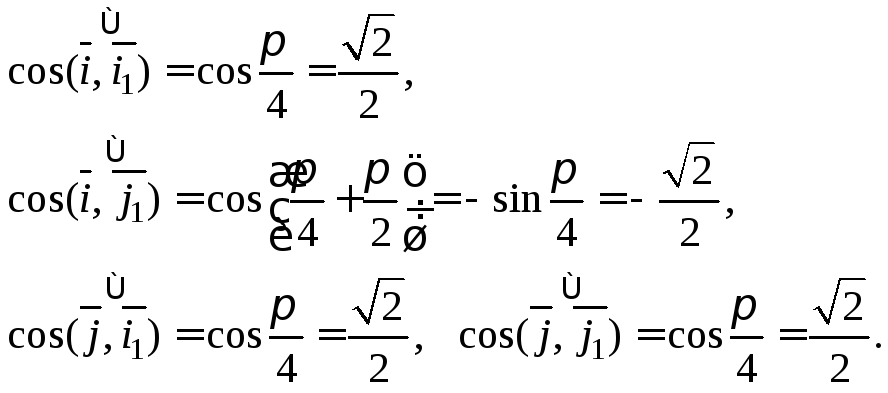
Это значит, что

откуда

Задания