
- •2 Заданы входная последовательность и импульсная характеристика дискретной системы Вычислить дискретную линейную свертку. Построить график свертки.
- •3 Решить разностное уравнение c начальным условием , где входная последовательность, отклик линейной стационарной дискретной системы.
- •1 Изобразить произвольную дискретную последовательность, записанную в виде суммы взвешенных и задержанных цифровых единичных отсчетов,
- •3 Решить разностное уравнение c начальным условием , где входная последовательность, отклик линейной стационарной дискретной системы.
- •1 Изобразить произвольную дискретную последовательность, записанную в виде суммы взвешенных и задержанных цифровых единичных отсчетов,
- •11 Вычислить двумерное дкп массива данных размером Восстановить исходный массив, выполнив двумерное обратное дискретное косинусное преобразование (одкп), если
- •3 Решить разностное уравнение c начальным условием , где входная последовательность, отклик линейной стационарной дискретной системы.
Контрольные задания и список литературы по дисциплине «Математические методы цифровой обработки сигналов»
Контрольное задание № 1
1
Изобразить произвольную дискретную
последовательность ,
записанную в виде суммы взвешенных и
задержанных цифровых единичных отсчетов,
,
записанную в виде суммы взвешенных и
задержанных цифровых единичных отсчетов,
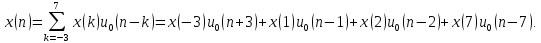
2
Заданы входная последовательность
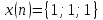 и импульсная характеристика дискретной
системы
и импульсная характеристика дискретной
системы
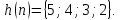 Вычислить дискретную линейную свертку.
Построить график свертки.
Вычислить дискретную линейную свертку.
Построить график свертки.
3
Решить разностное уравнение
 c
начальным условием
c
начальным условием
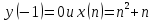 ,
где
,
где
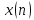 входная последовательность,
входная последовательность,
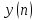 отклик линейной стационарной дискретной
системы.
отклик линейной стационарной дискретной
системы.
4
Вычислить комплексную частотную
характеристику (дискретизированное по
времени преобразование Фурье) рекурсивной
линейной дискретной системы, удовлетворяющей
разностному уравнению c
начальным условием
c
начальным условием
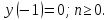 Вычислить модуль комплексной частотной
характеристики. Вычислить фазовую
характеристику системы. Построить
графики модуля и фазы как функции
нормированной частоты
Вычислить модуль комплексной частотной
характеристики. Вычислить фазовую
характеристику системы. Построить
графики модуля и фазы как функции
нормированной частоты
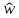 в диапазоне
в диапазоне
 где
где
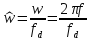 ,
,
 – циклическая и линейная частоты,
– циклическая и линейная частоты,
 -
частота дискретизации.
-
частота дискретизации.
5
Вычислить элементы системы дискретных
экспоненциальных функций (ДЭФ) и записать
ее в виде матрицы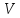 размером
размером
 Матрицу представить в алгебраической
и экспоненциальной форме.
Матрицу представить в алгебраической
и экспоненциальной форме.
6
Выполнить прямое дискретное преобразование
Фурье (ДПФ) последовательности
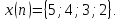 Восстановить исходную последовательность
через вычисление обратного ДПФ
последовательности коэффициентов
дискретного преобразования Фурье
Восстановить исходную последовательность
через вычисление обратного ДПФ
последовательности коэффициентов
дискретного преобразования Фурье
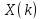 .
.
7
Дана последовательность
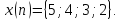 Применить быстрое преобразование Фурье
(БПФ) для вычисления коэффициентов ДПФ.
Показать, что алгоритм БПФ можно применять
для восстановления
Применить быстрое преобразование Фурье
(БПФ) для вычисления коэффициентов ДПФ.
Показать, что алгоритм БПФ можно применять
для восстановления
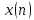 по коэффициентам ДПФ используемым в
качестве исходного массива данных.
Оценить вычислительную сложность
алгоритма БПФ.
по коэффициентам ДПФ используемым в
качестве исходного массива данных.
Оценить вычислительную сложность
алгоритма БПФ.
8
Заданы последовательности
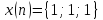 и
и
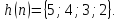 Вычислить линейную дискретную свертку
последовательностей с помощью ДПФ.
Построить график свертки.
Вычислить линейную дискретную свертку
последовательностей с помощью ДПФ.
Построить график свертки.
9
Вычислить ядро дискретного косинусного
преобразования (ДКП) размером
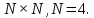 Матрицу представить в тригонометрической
и алгебраической и форме.
Матрицу представить в тригонометрической
и алгебраической и форме.
10
Выполнить прямое ДКП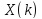 последовательности
последовательности
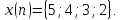 Изобразить график функции
Изобразить график функции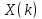 .
Восстановить исходную последовательность
через вычисление обратного ДКП
последовательности коэффициентов
дискретного косинусного преобразования
.
Восстановить исходную последовательность
через вычисление обратного ДКП
последовательности коэффициентов
дискретного косинусного преобразования
 .
.
11
Вычислить двумерное ДКП массива данных
 размером
размером
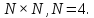 Восстановить исходный массив, выполнив
двумерное обратное дискретное косинусное
преобразование (ОДКП), если
Восстановить исходный массив, выполнив
двумерное обратное дискретное косинусное
преобразование (ОДКП), если

12 Вычислить среднеквадратичную ошибку восстановления исходных данных (задача 11) при обнулении 75% наименьших по значениям коэффициентов преобразования ДКП и последующем выполнении ОДКП над полученным массивом.
Контрольное задание № 2
1
Дана дискретная последовательность
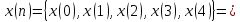
 Записать
выражение в виде суммы взвешенных и
задержанных цифровых единичных отсчетов,
определяющее значение отсчета с номером
Записать
выражение в виде суммы взвешенных и
задержанных цифровых единичных отсчетов,
определяющее значение отсчета с номером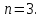
2 Заданы входная последовательность и импульсная характеристика дискретной системы Вычислить дискретную линейную свертку. Построить график свертки.
3 Решить разностное уравнение c начальным условием , где входная последовательность, отклик линейной стационарной дискретной системы.
4
Вычислить импульсную характеристику
идеального фильтра нижних частот (ФНЧ)
с частотой среза
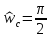 ,
если его частотная характеристика,
равная на промежутке [
,
если его частотная характеристика,
равная на промежутке [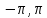 ]
]
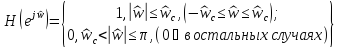 ,
,
вне
этого интервала вычисляется по
периодичности. Здесь
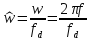 - это нормированная частота, а
- это нормированная частота, а
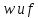 - это циклическая и линейная частоты,
- это циклическая и линейная частоты,
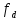 -
частота дискретизации, нормированная
частота среза ФНЧ
-
частота дискретизации, нормированная
частота среза ФНЧ
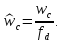
5
Вычислить элементы системы дискретных
экспоненциальных функций (ДЭФ) и записать
систему в виде матрицы размером
размером
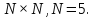 Матрицу представить в алгебраической
и экспоненциальной форме.
Матрицу представить в алгебраической
и экспоненциальной форме.
6
Выполнить прямое дискретное преобразование
Фурье (ДПФ) последовательности
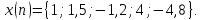 Восстановить исходную последовательность
через вычисление обратного ДПФ
последовательности коэффициентов
дискретного преобразования Фурье
Восстановить исходную последовательность
через вычисление обратного ДПФ
последовательности коэффициентов
дискретного преобразования Фурье
 .
.
7
Дана последовательность
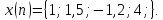 Применить быстрое преобразование Фурье
(БПФ) для вычисления коэффициентов ДПФ.
Показать, что алгоритм БПФ можно применять
для восстановления
Применить быстрое преобразование Фурье
(БПФ) для вычисления коэффициентов ДПФ.
Показать, что алгоритм БПФ можно применять
для восстановления
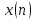 по коэффициентам ДПФ используемым в
качестве исходного массива данных.
Оценить вычислительную сложность
алгоритма БПФ.
по коэффициентам ДПФ используемым в
качестве исходного массива данных.
Оценить вычислительную сложность
алгоритма БПФ.
8
Заданы последовательности
 и
и
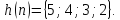 Вычислить линейную дискретную свертку
последовательностей с помощью ДПФ.
Построить график свертки
Вычислить линейную дискретную свертку
последовательностей с помощью ДПФ.
Построить график свертки
9
Вычислить ядро (матрицу)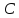 дискретного косинусного преобразования
(ДКП) размером
дискретного косинусного преобразования
(ДКП) размером
 Матрицу представить в тригонометрической
и числовой форме.
Матрицу представить в тригонометрической
и числовой форме.
10
Выполнить прямое ДКП последовательности
последовательности
 Изобразить график функции
Изобразить график функции .
Восстановить исходную последовательность
через вычисление обратного ДКП
последовательности коэффициентов
дискретного косинусного преобразования
.
Восстановить исходную последовательность
через вычисление обратного ДКП
последовательности коэффициентов
дискретного косинусного преобразования
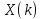 .
.
11
Вычислить двумерное ДКП массива данных
 размером
размером
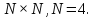 Восстановить исходный массив, выполнив
двумерное обратное дискретное косинусное
преобразование (ОДКП), если
Восстановить исходный массив, выполнив
двумерное обратное дискретное косинусное
преобразование (ОДКП), если

12 Вычислить среднеквадратичную ошибку восстановления исходных данных (задача 11) при обнулении 50% наименьших по значениям коэффициентов преобразования ДКП и последующем выполнении ОДКП над полученным массивом.
Контрольное задание № 3
1
Покажите, что дискретная система,
описываемая уравнением
 является линейной.
является линейной.
2
Вычислить линейную свертку двух
дискретных последовательностей, где
 ,
,
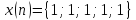 .
Построить график свертки.
.
Построить график свертки.
3
Показать, что разностное уравнение
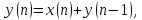 c
начальным условием
c
начальным условием
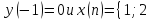 },
где
},
где
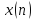 входная последовательность, описывает
отклик cумматора
входная последовательность, описывает
отклик cумматора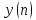
 .
.
4
Вычислить Фурье-образ (дискретизированное
по времени преобразование Фурье)
прямоугольного окна
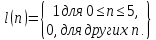 .
Вычислить ширину главного лепестка и
всех боковых лепестков Фурье-образа
прямоугольного окна
.
Вычислить ширину главного лепестка и
всех боковых лепестков Фурье-образа
прямоугольного окна
 Изобразить
график модуля комплексной частотной
характеристики окна.
Изобразить
график модуля комплексной частотной
характеристики окна.
5
Вычислить элементы системы дискретных
экспоненциальных функций (ДЭФ) и записать
систему в виде матрицы размером
размером
 Матрицу представить в алгебраической
и экспоненциальной форме.
Матрицу представить в алгебраической
и экспоненциальной форме.
6
Выполнить прямое дискретное преобразование
Фурье (ДПФ) последовательности
 Восстановить исходную последовательность
через вычисление обратного ДПФ
последовательности коэффициентов
дискретного преобразования Фурье
Восстановить исходную последовательность
через вычисление обратного ДПФ
последовательности коэффициентов
дискретного преобразования Фурье
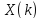 .
.
7
Дана последовательность
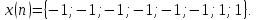 Применить быстрое преобразование Фурье
(БПФ) для вычисления коэффициентов ДПФ.
Показать, что алгоритм БПФ можно применять
для восстановления
Применить быстрое преобразование Фурье
(БПФ) для вычисления коэффициентов ДПФ.
Показать, что алгоритм БПФ можно применять
для восстановления
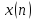 по коэффициентам ДПФ используемым в
качестве исходного массива данных.
Оценить вычислительную сложность
алгоритма БПФ.
по коэффициентам ДПФ используемым в
качестве исходного массива данных.
Оценить вычислительную сложность
алгоритма БПФ.
8
Заданы последовательности
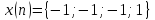 и
и
 Вычислить циклическую дискретную
свертку последовательностей с помощью
ДПФ. Построить график свертки.
Вычислить циклическую дискретную
свертку последовательностей с помощью
ДПФ. Построить график свертки.
9
Вычислить ядро (матрицу)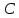 дискретного косинусного преобразования
(ДКП) размером
дискретного косинусного преобразования
(ДКП) размером
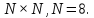 Матрицу представить в тригонометрической
и числовой форме.
Матрицу представить в тригонометрической
и числовой форме.
10
Выполнить прямое ДКП
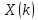 последовательности
последовательности
 Изобразить график функции
Изобразить график функции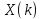 .
Восстановить исходную последовательность
через вычисление обратного ДКП
последовательности коэффициентов
дискретного косинусного преобразования
.
Восстановить исходную последовательность
через вычисление обратного ДКП
последовательности коэффициентов
дискретного косинусного преобразования
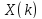 .
.
11
Вычислить двумерное ДКП массива данных
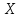 размером
размером
 Восстановить исходный массив, выполнив
двумерное обратное дискретное косинусное
преобразование (ОДКП), если
Восстановить исходный массив, выполнив
двумерное обратное дискретное косинусное
преобразование (ОДКП), если

12 Вычислить среднеквадратичную ошибку восстановления исходных данных (задача 11) при обнулении 50% наименьших по значениям коэффициентов преобразования ДКП и последующем выполнении ОДКП над полученным массивом.
Контрольное задание № 4
1
Покажите, что дискретная система c
входным воздействием
 и откликом
и откликом
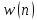 ,
описываемая уравнением
,
описываемая уравнением
 ,
является нелинейной.
,
является нелинейной.
2
Вычислить линейную свертку двух
дискретных последовательностей, где
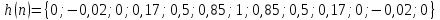 ,
,
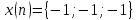 .
Построить график свертки.
.
Построить график свертки.
3
Показать, что разностное уравнение
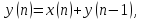 c
начальным условием
c
начальным условием
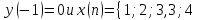 },
где
},
где
 входная последовательность, описывает
отклик cумматора
входная последовательность, описывает
отклик cумматора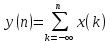 .
.
4
Вычислить Фурье-образ (дискретизированное
по времени преобразование Фурье)
последовательности
где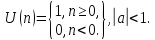 Построить
графики модуля и фазы как функции
нормированной частоты
Построить
графики модуля и фазы как функции
нормированной частоты
 в диапазоне
в диапазоне
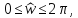 где
где
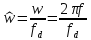 ,
,
 – циклическая и линейная частоты,
– циклическая и линейная частоты,
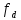 -
частота дискретизации.
-
частота дискретизации.
5
Вычислить элементы системы дискретных
экспоненциальных функций (ДЭФ) и записать
систему в виде матрицы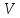 размером
размером
 Матрицу представить в алгебраической
и экспоненциальной форме.
Матрицу представить в алгебраической
и экспоненциальной форме.
6
Выполнить прямое дискретное преобразование
Фурье (ДПФ) последовательности
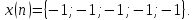 Восстановить исходную последовательность
через вычисление обратного ДПФ
последовательности коэффициентов
дискретного преобразования Фурье
Восстановить исходную последовательность
через вычисление обратного ДПФ
последовательности коэффициентов
дискретного преобразования Фурье
 .
.
7
Дана последовательность
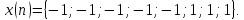 Применить быстрое преобразование Фурье
(БПФ) для вычисления коэффициентов ДПФ.
Показать, что алгоритм БПФ можно применять
для восстановления
Применить быстрое преобразование Фурье
(БПФ) для вычисления коэффициентов ДПФ.
Показать, что алгоритм БПФ можно применять
для восстановления
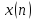 по коэффициентам ДПФ используемым в
качестве исходного массива данных.
Оценить вычислительную сложность
алгоритма БПФ.
по коэффициентам ДПФ используемым в
качестве исходного массива данных.
Оценить вычислительную сложность
алгоритма БПФ.
8
Заданы последовательности
 и
и
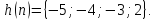 Вычислить циклическую дискретную
свертку последовательностей с помощью
ДПФ. Построить график свертки.
Вычислить циклическую дискретную
свертку последовательностей с помощью
ДПФ. Построить график свертки.
9
Вычислить ядро (матрицу)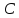 дискретного косинусного преобразования
(ДКП) размером
дискретного косинусного преобразования
(ДКП) размером
 Матрицу представить в тригонометрической
и числовой форме.
Матрицу представить в тригонометрической
и числовой форме.
10
Выполнить прямое ДКП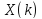 последовательности
последовательности
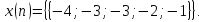 Изобразить график функции
Изобразить график функции .
Восстановить исходную последовательность
через вычисление обратного ДКП
последовательности коэффициентов
дискретного косинусного преобразования
.
Восстановить исходную последовательность
через вычисление обратного ДКП
последовательности коэффициентов
дискретного косинусного преобразования
 .
.
11
Вычислить двумерное ДКП массива данных
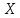 размером
размером
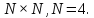 Восстановить исходный массив, выполнив
двумерное обратное дискретное косинусное
преобразование (ОДКП), если
Восстановить исходный массив, выполнив
двумерное обратное дискретное косинусное
преобразование (ОДКП), если
12 Вычислить среднеквадратичную ошибку восстановления исходных данных (задача 11) при обнулении 12,5 % наименьших по значениям коэффициентов преобразования ДКП и последующем выполнении ОДКП над полученным массивом.
Контрольное задание № 5
1
Вычислить импульсную характеристику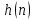 дискретной рекурсивной системы для
входа
дискретной рекурсивной системы для
входа
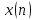 .
Соотношение вход-выход системы описывается
разностным уравнением
.
Соотношение вход-выход системы описывается
разностным уравнением
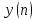 с постоянными коэффициентами
с постоянными коэффициентами
 .
.
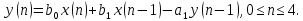
2
Вычислить линейную свертку двух
дискретных последовательностей, где
 импульсная характеристика цифровой
системы,
импульсная характеристика цифровой
системы,
 .
Построить график свертки.
.
Построить график свертки.
3
Решить разностное уравнение
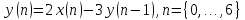 c
начальным условием
c
начальным условием
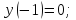
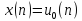 цифровой единичный импульс,
цифровой единичный импульс,
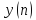 отклик рекурсивной линейной дискретной
системы.
отклик рекурсивной линейной дискретной
системы.
4
Показать, что Фурье-образ (дискретизированное
по времени преобразование Фурье)
последовательности
 ,
,
где равен
равен
 .
Построить графики модуля и фазы как
функции нормированной частоты
.
Построить графики модуля и фазы как
функции нормированной частоты
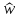 в диапазоне
в диапазоне
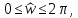 где
где
 ,
,
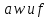 – циклическая и линейная частоты,
– циклическая и линейная частоты,
 -
частота дискретизации.
-
частота дискретизации.
5
Вычислить элементы системы дискретных
экспоненциальных функций (ДЭФ) и записать
систему в виде матрицы размером
размером
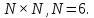 Матрицу представить в алгебраической
и экспоненциальной форме.
Матрицу представить в алгебраической
и экспоненциальной форме.
6
Выполнить прямое дискретное преобразование
Фурье (ДПФ) последовательности
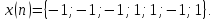 Восстановить исходную последовательность
через вычисление обратного ДПФ
последовательности коэффициентов
дискретного преобразования Фурье
Восстановить исходную последовательность
через вычисление обратного ДПФ
последовательности коэффициентов
дискретного преобразования Фурье
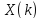 .
.
7
Дана последовательность
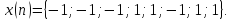 Применить быстрое преобразование Фурье
(БПФ) для вычисления коэффициентов ДПФ.
Показать, что алгоритм БПФ можно применять
для восстановления
Применить быстрое преобразование Фурье
(БПФ) для вычисления коэффициентов ДПФ.
Показать, что алгоритм БПФ можно применять
для восстановления
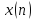 по коэффициентам ДПФ используемым в
качестве исходного массива данных.
Оценить вычислительную сложность
алгоритма БПФ.
по коэффициентам ДПФ используемым в
качестве исходного массива данных.
Оценить вычислительную сложность
алгоритма БПФ.
8
Задана последовательность
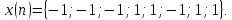 Вычислить циклическую дискретную
автосвертку последовательности с
помощью ДПФ. Построить график свертки.
Вычислить циклическую дискретную
автосвертку последовательности с
помощью ДПФ. Построить график свертки.
9
Вычислить ядро (матрицу) дискретного косинусного преобразования
(ДКП) размером
дискретного косинусного преобразования
(ДКП) размером
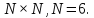 Матрицу представить в тригонометрической
и числовой форме.
Матрицу представить в тригонометрической
и числовой форме.
10
Выполнить прямое ДКП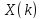 последовательности
последовательности
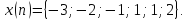 Изобразить график функции
Изобразить график функции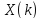 .
Восстановить исходную последовательность
через вычисление обратного ДКП
последовательности коэффициентов
дискретного косинусного преобразования
.
Восстановить исходную последовательность
через вычисление обратного ДКП
последовательности коэффициентов
дискретного косинусного преобразования
 .
.
11
Вычислить двумерное ДКП массива данных
 размером
размером
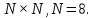 Восстановить исходный массив, выполнив
двумерное обратное дискретное косинусное
преобразование (ОДКП), если
Восстановить исходный массив, выполнив
двумерное обратное дискретное косинусное
преобразование (ОДКП), если

12 Вычислить среднеквадратичную ошибку восстановления исходных данных (задача 11) при обнулении 50% наименьших по значениям коэффициентов преобразования ДКП и последующем выполнении ОДКП над полученным массивом.
Контрольное задание № 6
1
Вычислить импульсную характеристику
дискретной рекурсивной системы для
входа
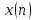 .
Соотношение вход-выход системы описывается
разностным уравнением
.
Соотношение вход-выход системы описывается
разностным уравнением
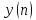 с коэффициентом
с коэффициентом
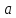 .
.

2
Вычислить отклик линейной дискретной
системы по формуле свертки. Заданы
импульсная характеристика
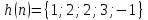 и входное воздействие
и входное воздействие
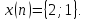
Построить график свертки.
3
Записать разностное уравнение рекурсивной
линейной дискретной системы второго
порядка. Вычислить отклик
 этой системы c
начальным условием
этой системы c
начальным условием
 для
значений
для
значений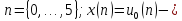 цифровой единичный импульс.
цифровой единичный импульс.
4
Вычислить модуль и фазу Фурье-образа
(дискретизированное по времени
преобразование Фурье) последовательности
 ,
,
где Построить
графики модуля и фазы как функции
нормированной частоты
Построить
графики модуля и фазы как функции
нормированной частоты
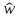 в диапазоне
в диапазоне
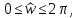 где
где
 ,
,
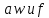 – циклическая и линейная частоты,
– циклическая и линейная частоты,
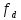 -
частота дискретизации.
-
частота дискретизации.
5
Вычислить элементы системы дискретных
экспоненциальных функций (ДЭФ) и записать
систему в виде матрицы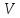 размером
размером
 Матрицу представить в алгебраической
и экспоненциальной форме.
Матрицу представить в алгебраической
и экспоненциальной форме.
6
Выполнить прямое дискретное преобразование
Фурье (ДПФ) последовательности
 Восстановить исходную последовательность
через вычисление обратного ДПФ
последовательности коэффициентов
дискретного преобразования Фурье
Восстановить исходную последовательность
через вычисление обратного ДПФ
последовательности коэффициентов
дискретного преобразования Фурье
 .
.
7Дана
последовательность
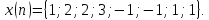 Применить быстрое преобразование Фурье
(БПФ) для вычисления коэффициентов ДПФ.
Показать, что алгоритм БПФ можно применять
для восстановления
Применить быстрое преобразование Фурье
(БПФ) для вычисления коэффициентов ДПФ.
Показать, что алгоритм БПФ можно применять
для восстановления
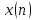 по коэффициентам ДПФ используемым в
качестве исходного массива данных.
Оценить вычислительную сложность
алгоритма БПФ.
по коэффициентам ДПФ используемым в
качестве исходного массива данных.
Оценить вычислительную сложность
алгоритма БПФ.
8
Задана последовательность
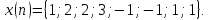 Вычислить циклическую дискретную
автосвертку последовательности
Вычислить циклическую дискретную
автосвертку последовательности
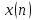 с помощью ДПФ. Построить график свертки.
с помощью ДПФ. Построить график свертки.
9
Вычислить ядро (матрицу) дискретного косинусного преобразования
(ДКП) размером
дискретного косинусного преобразования
(ДКП) размером
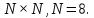 Матрицу представить в тригонометрической
и числовой форме.
Матрицу представить в тригонометрической
и числовой форме.
10
Выполнить прямое ДКП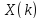 последовательности
последовательности
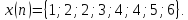 Изобразить график функции
Изобразить график функции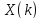 .
Восстановить исходную последовательность
через вычисление обратного ДКП
последовательности коэффициентов
дискретного косинусного преобразования
.
Восстановить исходную последовательность
через вычисление обратного ДКП
последовательности коэффициентов
дискретного косинусного преобразования
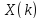 .
.
11
Вычислить двумерное ДКП массива данных
 размером
размером
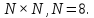 Восстановить исходный массив, выполнив
двумерное обратное дискретное косинусное
преобразование (ОДКП), если
Восстановить исходный массив, выполнив
двумерное обратное дискретное косинусное
преобразование (ОДКП), если
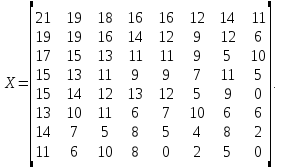
12 Вычислить среднеквадратичную ошибку восстановления исходных данных (задача 11) при обнулении 50% наименьших по значениям коэффициентов преобразования ДКП и последующем выполнении ОДКП над полученным массивом.
Контрольное задание № 7
1
Изобразить произвольную дискретную
последовательность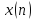 ,
записанную в виде суммы взвешенных и
задержанных цифровых единичных отсчетов,
,
записанную в виде суммы взвешенных и
задержанных цифровых единичных отсчетов,
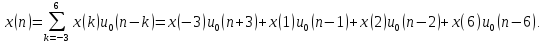
2
Вычислить отклик линейной дискретной
системы по формуле свертки. Заданы
импульсная характеристика
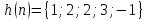 и входное воздействие
и входное воздействие
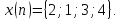 Построить график свертки.
Построить график свертки.
3
Вычислить импульсную характеристику
cумматора,
описываемого выражением
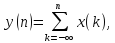 для
для
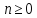 .
.
4
Вычислить комплексную частотную
характеристику (дискретизированное по
времени преобразование Фурье) рекурсивной
линейной дискретной системы, удовлетворяющей
разностному уравнению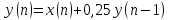 c
начальным условием
c
начальным условием
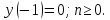 Вычислить модуль комплексной частотной
характеристики. Вычислить фазовую
характеристику системы. Построить
графики модуля и фазы как функции
нормированной частоты
Вычислить модуль комплексной частотной
характеристики. Вычислить фазовую
характеристику системы. Построить
графики модуля и фазы как функции
нормированной частоты
 в диапазоне
в диапазоне
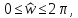 где
где
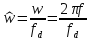 ,
,
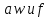 – циклическая и линейная частоты,
– циклическая и линейная частоты,
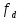 -
частота дискретизации.
-
частота дискретизации.
5
Представить в экспоненциальной и
алгебраической формах матрицы системы дискретных экспоненциальных
функций (ДЭФ) с минимальными фазами.
Размер
системы дискретных экспоненциальных
функций (ДЭФ) с минимальными фазами.
Размер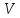 :
:
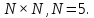
6
Выполнить прямое дискретное преобразование
Фурье (ДПФ) последовательности
 Восстановить исходную последовательность
через вычисление обратного ДПФ
последовательности коэффициентов
дискретного преобразования Фурье
Восстановить исходную последовательность
через вычисление обратного ДПФ
последовательности коэффициентов
дискретного преобразования Фурье
 .
.
7Дана
последовательность
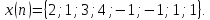 Применить быстрое преобразование Фурье
(БПФ) для вычисления коэффициентов ДПФ.
Показать, что алгоритм БПФ можно применять
для восстановления
Применить быстрое преобразование Фурье
(БПФ) для вычисления коэффициентов ДПФ.
Показать, что алгоритм БПФ можно применять
для восстановления
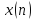 по коэффициентам ДПФ используемым в
качестве исходного массива данных.
Оценить вычислительную сложность
алгоритма БПФ.
по коэффициентам ДПФ используемым в
качестве исходного массива данных.
Оценить вычислительную сложность
алгоритма БПФ.
8
Задана последовательность
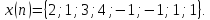 Вычислить циклическую дискретную
автосвертку последовательности
Вычислить циклическую дискретную
автосвертку последовательности
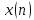 с помощью ДПФ. Построить график свертки.
с помощью ДПФ. Построить график свертки.
9
Вычислить ядро (матрицу) дискретного косинусного преобразования
(ДКП) размером
дискретного косинусного преобразования
(ДКП) размером
 Матрицу представить в тригонометрической
и числовой форме.
Матрицу представить в тригонометрической
и числовой форме.
10
Выполнить прямое ДКП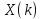 последовательности
последовательности
 Восстановить исходную последовательность
через вычисление обратного ДКП
последовательности коэффициентов
дискретного косинусного преобразования
Восстановить исходную последовательность
через вычисление обратного ДКП
последовательности коэффициентов
дискретного косинусного преобразования
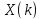 .
.
11
Вычислить двумерное ДКП массива данных
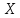 размером
размером
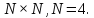 Изобразить график функции
Изобразить график функции .
Восстановить исходный массив, выполнив
двумерное обратное дискретное косинусное
преобразование (ОДКП), если
.
Восстановить исходный массив, выполнив
двумерное обратное дискретное косинусное
преобразование (ОДКП), если

12 Вычислить среднеквадратичную ошибку восстановления исходных данных (задача 11) при обнулении 68,75% наименьших по значениям коэффициентов преобразования ДКП и последующем выполнении ОДКП над полученным массивом.
Контрольное задание № 8
