
Метода ЦОС
.pdf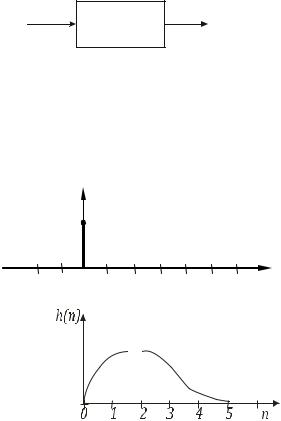
Решение. |
Пусть |
Для доказательства вычислим |
отклики |
и |
По определению сумматора имеем |
|
|
и |
Поменяем в последней сумме индекс суммирования на Напомним, что с изменением индекса суммирования изменяются пределы суммирования.
,
= Таким образом, сумматор является стационарной
системой.
3.4. Связь между входным и выходным сигналами в линейной системе
Наличие свойств линейности и стационарности позволяет представлять анализируемую систему в удобном виде. Предположим, на вход системы подан единичный импульс (отсчет)
Обычно выход линейной системы является запаздывающей и усиленной или подавленной версией входа. Отклик системы на этот сигнал обозначим
рисунок 3.3.
Линейная
система
Рисунок 3.3 – К определению импульсной характеристики
Выход системы, инициированный единичным импульсом, не будет тем же импульсом, а будет меняться со временем, в некоторый момент, достигая максимального значения, например, как показано на рисунке 3.4
1
–2 –1 0 1 2 3 4 5
Рисунок 3.4 ‒ Входной единичный импульс и импульсная характеристика системы
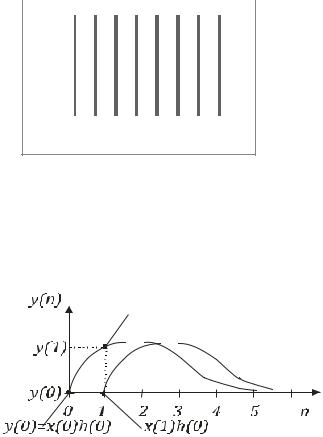
Из рисунка видно, что в момент времени 0 выход равен |
В |
|||
момент времени |
выход равен |
Вход можно |
представить |
|
импульсом разной амплитуды (мощности). В момент времени |
подадим |
|||
на вход системы отсчет высотой |
. Поскольку входной сигнал увеличился |
|||
в |
раз, то согласно свойству линейной системы, отклик на этот сигнал |
|||
также увеличился в |
раз. Тогда выходной сигнал определяется отсчетами |
|||
, |
|
|
|
|||||||||
. |
|
|
|
|||||||||
Пусть теперь на вход подается последовательность импульсов |
, рисунок |
|||||||||||
3.5. |
|
|
|
|
|
|
|
|
|
|
|
|
|
n) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n
Рисунок 3.5
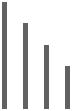
В этом случае на каждое импульсное воздействие формируется отклик, соответствующий импульсной характеристике системы. Выход системы получается из отдельных импульсных откликов, рисунок 3.6.
x(0)h(1)
|
|
Рисунок 3.6 |
|
Из рисунка видно, что в момент времени 0 выход равен |
. В |
||
следующий момент времени |
выход состоит из суммы двух компонент: |
||
первое слагаемое ‒ это |
(из-за текущего импульса |
и второе |
|
слагаемое ‒ |
(из-за запаздывающего влияния входа в момент |
||
времени |
. Выходной сигнал системы в момент времени |
равен |
|

Последующие выходы запишутся как
Выводы
1.Если система линейна, выход можно записать как линейную сумму влияния предыдущих входов.
2.Выход получается умножением входной последовательности на соответствующие отсчеты, обращенной во времени функции импульсной характеристики.
3.Учитывая свойство линейности и возможность представления любой последовательности в форме линейной комбинации сдвинутых единичных импульсов (2.12), можно утверждать, что линейная стационарная система определяется своей реакцией на единичный импульс или импульсной характеристикой при нулевых начальных условиях.
Замечание. Признаком нулевых начальных условий является отсутствие отклика при отсутствии входной последовательности
Если начальный момент времени обозначим |
, то ему соответствует |
п и |
(3.6) |
Нулевые начальные условия отвечают принципу причинности, в соответствии с которым отклик не может возникнуть раньше воздействия.
Для описания во временной области линейных стационарных дискретных систем широко применяются следующие линейные уравнения (формулы):
‒свертка, где используется импульсная характеристика;
‒разностные уравнения, где используются параметры линейных дискретных систем (ЛДС).
3.5. Уравнение свертки
Из свойств стационарности (инвариантности к сдвигу) следует, что откликом на последовательность будет , рисунок 3.7.
Рисунок 3.7
Рассмотрим отклик ЛДС на входную последовательность, представленную в виде (2.12)
Из свойств линейности и стационарности ЛДС следует, что откликом на эту последовательность должна быть последовательность
|
|
= |
|
(3.7) |
Если |
последовательность, |
значения которой зависят от отсчетов двух |
||
последовательностей |
и |
и определяется выражением (3.7), то |
||
говорят, что |
есть свертка. Обозначение операции свертка |
|||
|
|
|
|
(3.8) |
Заменяя индекс суммирования в (3.7), получаем другое выражение свертки.
Пусть |
Тогда |
|
|
|
= |
= |
(3.9) |
Таким образом, линейная инвариантная к сдвигу дискретная система с
входом |
и импульсной характеристикой |
имеет тот же выход, что и |
|||
линейная |
инвариантная к сдвигу |
дискретная |
система с входом |
и |
|
импульсной характеристикой |
. |
|
|
|
|
С учетом нулевых начальных условий (3.6) линейные уравнения (3.7) и |
|||||
(3.9) представляются в виде |
|
|
|
|
|
|
|
|
|
|
(3.10) |
|
|
|
|
|
(3.11) |
Согласно этим формулам отклик |
|
вычисляется как дискретная свертка |
|||
воздействия и импульсной характеристики. Покажем тождественность результатов вычисления по формуле свертки в двух вариантах ее записи
(3.10) и (3.11). Определим значение коэффициента свертки в точке |
По |
формуле (3.11) имеем |
|
По формуле (3.11) получаем результат
Выбор варианта свертки определяется удобством применения. Операцию вычисления дискретной свертки по формуле (3.7) и (3.9) называют линейной (апериодической) сверткой. Из формул свертки следует, что , т.е. -й член выходной последовательности получается в результате умножения входной
последовательности (записанной как функция от |
) на последовательность |
|
. |
Затем при каждом фиксированном суммируются |
|
все произведения |
c параметром |
в качестве параметра |
суммирования. Следовательно, при свертке двух последовательностей для
вычисления n -го члена последовательности |
используются все отсчеты |
|
входной последовательности |
и |
|
3.5.1. Графическое представление свертки
Cвертка – это одна из наиболее используемых операций в ЦОС. Например, это основная операция цифровой фильтрации. Для более полного понимания формулы свертки рассмотрим процесс образования последовательности значностью . На рисунке 3.8.а показана последовательность
|
|
h(k) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-4 -3 -2 -1 0 1 2 3 4 |
|
|||||||||
|
|
|
|
|
|
k |
|
|||||
|
|
|
|
|
|
|||||||
|
|
|
|
Рисунок 3.8.а |
|
|||||||
Определим последовательность |
. Форма этой |
|||||||||||
последовательности показана на рисунке 3.8.б. |
|
|||||||||||
Например, если |
|
, то |
; |
|||||||||
|
и т.д. |
|
||||||||||

h(-k)
-4 -3 -2 -1 0 1 2 3 4 k
Рисунок 3.8.б
Далее определим последовательность
Форма этой последовательности для |
показана на рисунке 3.8.в |
||
Например, если |
имеем |
|
|
Для |
получаем |
|
|
Для |
получаем |
|
|
|
|
и т.д. |
|
h(n-k)
|
|
|
k |
|
|
|
|
|
|
|
|
Рисунок 3.8.в |
|
|
Вывод. Для вычисления последовательности |
|
|||
необходимо: |
|
|
|
|
– обратить по времени последовательность |
относительно точки |
|||
для получения последовательности |
|
|||
– cдвинуть последовательность |
на интервалов дискретизации |
|||
вправо. |
|
|
|
|
Пример |
3.6. |
Задана |
входная |
последовательность |
|
|
и |
импульсная |
характеристика ЛДС |
|
|
|
Вычислим свертку. На рисунках |
|
3.9.а – 3.9.г. показаны этапы вычислений.

x(k)
-4 -3 -2 -1 0 1 2 3 4 k
Рисунок 3.9.а
h(k)
|
|
k |
|
|
|
|
|
Рисунок 3.9.б |
Для |
по формуле свертки вычисляем |
|
Условно процесс вычисления свертки отображается на рисунке 3.9.в. и Временное соотношение сворачиваемых отсчетов показано ниже
1 1 1
2 3 4 5
5.
h(-k)
x(k)
k
|
Рисунок 3.9.в |
Для |
по формуле свертки вычисляем |
Условно процесс вычисления свертки отображается на рисунке 3.9.г. и Временное соотношение сворачиваемых отсчетов показано ниже
1 1 1
2 3 4 5
4+5 = 9.
h(-k)
x(k)
k
Рисунок 3.9.г Действуя аналогичным образом, вычисляем остальные коэффициенты свертки.
1 1 1
2 3 4 5 3+4+5=12.
1 1 1
2 3 4 5 2+3+4=9.
1 1 1
2 3 4 5
|
|
2+3=5. |
|
|
|
|
1 1 1 |
|
|
|
|
2 3 4 |
5 |
|
|
|
2. |
|
|
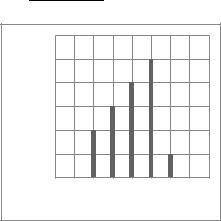
На рисунке 3.10 показана реакция линейной дискретной системы с |
||||
импульсной |
характеристикой |
|
на |
входную |
последовательность |
. |
|
|
|
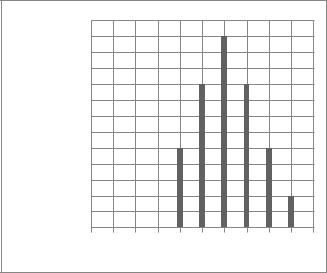
y(n)
-4 -3 -2 -1 0 1 |
2 3 4 5 6 |
n |
|
Рисунок 3.10 – Реакция линейной дискретной системы
Из рассмотренного механизма вычисления свертки следуют следующие выводы:
–если длительность входной последовательности и (или) импульсной характеристики бесконечна, длительность отклика также бесконечна;
–если длительность входной последовательности и импульсной
характеристики конечны и равны |
и |
, |
то длительность отклика также |
||||
конечна и равна |
; при |
|
|
|
|
|
|
Для конечных последовательностей |
|
и |
формулы |
свертки |
в |
двух |
|
вариантах записи приобретают вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.12) |
|
|
|
|
|
|
|
(3.13) |
|
Упражнения |
|
|
|
|
|
|
|
3.2. Вычислить линейную свертку двух дискретных конечных |
|
|
|||||
последовательностей |
|
|
|
|
|
|
|
и |
|
|
|
|
, где |
– |
|
импульсная характеристика |
дискретной |
системы, |
– |
входная |
|||
последовательность. Построить график свертки.
3.3. Вычислить отклик ЛДС по формуле свертки. Изобразить график
свертки. Задана импульсная характеристика |
и входное |
воздействие |
|
3.4. Найти реакцию ЛДС на единичный импульс: |
|
а) идеальной системы задержки |
|
б) сумматора |
|
3.6. Устойчивость линейных дискретных систем |
|
Определение 3.1. Линейная дискретная система называется устойчивой, если и только если ее реакция на любой ограниченный по амплитуде
сигнал ограничен. Последовательность |
называется ограниченной, если |
найдется такое положительное число |
не равное бесконечности, что |
|
. |
Таким образом, для устойчивой системы отклик
|
. |
|
Пример 3.7. Покажем, что система без запоминания (пример 3.2) |
||
устойчива. |
Для доказательства предположим, что |
для всех |
Тогда |
. Следовательно, система устойчива. |
|
Определение 3.2. Линейная стационарная система является устойчивой тогда и только тогда, когда ее импульсная характеристика, абсолютно суммируемая последовательность, т.е. если
. |
(3.14) |
Рассмотрим примеры, отражающие свойство устойчивости стационарной системы.
Пример 3.7. Для системы идеальной задержки |
отклик |
на единичный импульс |
|
|
. |
В этом примере импульсная характеристика имеет конечное число отсчетов (один ненулевой отсчет при Такие системы называются системами с конечной импульсной характеристикой – КИХ фильтрами.
Пример 3.8. Для сумматора |
отклик на единичный |
импульс |
|
|
(3.15) |
где – единичный скачок На рисунке 3.11 изображен единичный скачок Импульсная
характеристика сумматора не ограничена по времени. Характеристика формируется только тактовой последовательностью импульсов. Системы с неограниченной по длительности импульсной характеристикой называются системами с бесконечной импульсной характеристикой – БИХ фильтрами.
