
Метода ЦОС
.pdf
частотой дискретизации |
1000 гц |
На рисунке 4.7 показан график фазы как функция частоты в диапазоне
|
360 |
|
|
|
|
|
|
180 |
|
|
|
|
|
φ |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
-180 |
0 |
π/ |
π |
π/ |
π |
|
-360 |
|
|
|
|
|
|
-540 |
|
|
|
|
|
|
-720 |
|
|
|
|
|
|
-900 |
|
|
|
ω |
|
|
|
|
|
|
|
Рисунок 4.7– Фазо-частотная характеристика системы
Фаза-частотную характеристику |
можно |
выразить и как |
|
функцию линейной частоты, измеряемой в герцах. Значению фазы |
|||
соответствует |
|
Пусть |
, |
|
|||
Фазовая характеристика идеальной системы задержки в диапазоне имеет вид, показанный на рисунке 4.8.
|
360 |
|
|
|
|
|
|
180 |
|
|
|
|
|
φ |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
-180 |
0 |
250 |
500 |
750 |
1000 |
|
-360 |
|
|
|
|
|
|
-540 |
|
|
|
|
|
|
-720 |
|
|
|
|
|
|
-900 |
|
|
|
f |
|
|
|
|
|
|
|
Рисунок 4.8 – Фазо-частотная характеристика системы
Пример 4.2. Вычислить комплексную частотную характеристику рекурсивной линейной дискретной системы с постоянными параметрами, удовлетворяющей разностному уравнению c начальным условием:
Решение. Воспользуемся результатом вычисления импульсной характеристики упражнения 3.7. Коэффициенты . Тогда частотная характеристика данной системы определяется из выражения
(4.12)

Если , то формула (4.12) представляет собой сумму бесконечно убывающей геометрической прогрессии, которая сходится. Сумма такой прогрессии выражается формулой
где |
– первый член последовательности |
прогрессии, |
– знаменатель |
||||||
геометрической прогрессии. В примере |
(для |
, |
. Тогда |
||||||
|
|
|
|
|
|
|
|
|
(4.13) |
Соотношение (4.13) перепишем как |
|
|
|
|
|||||
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
, |
где |
. |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|||
Модуль комплексной частотной характеристики определяется как
Фазовая характеристика системы записывается как
.
Напомним, аргумент комплексного числа определяется с точностью до слагаемого , где любое целое число.
Так как , аргумент действительного положительного числа имеет главное значение ноль:
.
Следовательно, .
.
На рисунке 4.9 изображены модуль |
и фаза |
как функции |
|
нормированной частоты в диапазоне |
при |
и |
. |
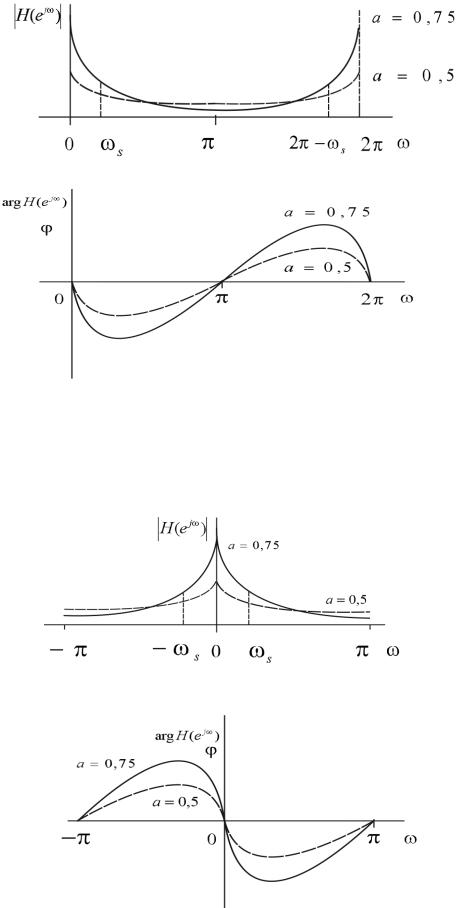
Рисунок 4.9 – Комплексная частотная характеристика рекурсивной линейной системы первого порядка
На полуинтервале |
функции |
и |
изображены на рисунке 4.10. |
|
|
Рисунок 4.10 – Комплексная частотная характеристика фильтра нижних частот
Как видно, функция является характеристикой фильтра нижних частот (ФНЧ).
Можно показать, что рекурсивная линейная система второго порядка
вида
будет иметь частотную характеристику цифрового резонатора.
4.5. Дискретизированное по времени преобразование Фурье
Произвольную входную дискретную последовательность вещественных или
комплексных чисел |
можно представить в виде интеграла Фурье |
|
||
|
|
|
, |
(4.14) |
|
|
|||
где |
|
|
|
(4.15) |
дискретизированное по времени прямое преобразование Фурье
последовательности |
или Фурье-образ последовательности |
. |
||
Преобразование |
называют также спектральной функцией. |
|
||
Формула (4.14) определяет понятие обратное преобразование Фурье |
||||
спектральной |
функции |
. Поскольку |
непрерывная |
|
периодическая функция частоты, она может быть выражена рядом Фурье. Тогда формула (4.15) представляет собой разложение периодической
функции |
в виде ряда Фурье, в котором коэффициентами Фурье |
|||
являются значения отсчетов последовательности |
. |
|
||
Обратное преобразование Фурье (4.14) можно трактовать как |
||||
представление последовательности |
через непрерывную периодическую |
|||
функцию частоты |
. А именно, |
последовательность |
можно |
|
рассматривать в виде суперпозиции (интеграла) экспоненциальных сигналов с комплексными амплитудами
Замечание. Пара преобразований Фурье существует только тогда, когда ряд (4.15) сходится.
Фурье-образ последовательности |
в алгебраической |
и показательной |
форме записывается как |
|
|
|
|
(4.16) |
|
. |
(4.17) |
Совокупность значений |
и |
характеризуют |
амплитудный спектр и фазовый спектр последовательности Сравнивая формулы (4.11) и (4.15), видим, что комплексная частотная
характеристика линейной дискретной системы есть Фурье-образ ее

импульсной характеристики. С помощью обратного преобразования Фурье комплексной частотной характеристики записывается импульсная характеристика системы
. (4.18)
4.6.Свойства дискретизированного по времени преобразования Фурье
4.6.1.Теорема о свертке
Ранее было показано, что отклик линейной стационарной системы на
последовательность |
определяется как |
|
, |
где множитель |
– комплексная частотная характеристика системы |
представляет комплексный коэффициент передачи для каждого значения частоты
Вычислим отклик линейной системы с импульсной характеристикой
на произвольную входную последовательность |
. |
В этом случае |
||
входная и выходная последовательность связаны соотношением свертки |
||||
|
|
|
, |
(4.19) |
где |
|
|
|
(4.20) |
|
|
|
||
Подставляя в (4.19) выражение для |
, получаем |
|
|
|
Напомним, |
в виде (4.20) есть суперпозиция комплексных экспонент. |
|
Тогда отклик |
линейной стационарной системы на |
является |
суперпозицией откликов на каждую комплексную экспоненту, входящую в представление сигнала Так как отклик на каждую комплексную экспоненту получается умножением на комплексный коэффициент
пропорциональности |
, зависящий от значения |
частоты |
, а |
||
промежуток интегрирования совпадает с периодом функции |
, можно |
||||
записать |
|
|
|
|
|
|
|
|
|
|
|
|
(4.21) |
|
|
||
Обозначив |
|
|
|
|
|
|
, |
|
(4.22) |
||
получаем комплексную частотную характеристику свертки. Формула (4.22) отражает связь между входом и выходом в частотной

области. Выражение (4.22) – одно из важнейших свойств преобразования Фурье. Соотношение (4.21) записанное в виде
(4.23)
представляет собой обратное преобразования Фурье от Фурье-образа свертки.
Вывод. Связь между входом и выходом линейной системы, представленная как операция свертки во временной области, в частотной области представляется операцией произведения.
Замечание. Если дискретная система нелинейна и нестационарна, получить общее соотношение между Фурье-образами ее входной и выходной последовательностью довольно сложно.
4.6.2. Теорема о периодической свертке, или модуляция
Вычислим Фурье-образ от произведения двух последовательностей.
Пусть последовательности |
и |
имеют соответственно Фурье-образы |
||
|
|
|
, |
|
|
|
|
. |
|
Сформируем последовательность |
. Здесь |
есть |
||
результат перемножения двух последовательностей – процесс модуляции.
Фурье-образ последовательности |
определяется из выражения |
|
|
. |
(4.24) |
Выразим Фурье-образ от произведения двух последовательностей через обратное преобразование Фурье последовательности
(4.25)
Подставляя в (4.24) значение (4.25), получаем
С учетом линейности и стационарности дискретной системы, свойства однородности, можно записать последнее выражение в виде

(4.26)
Правая часть уравнения является периодической сверткой двух периодических функций в частотной области. Промежуток интегрирования свертки совпадает с периодом подынтегральных функций. Как следует из (4.26), произведению дискретных последовательностей соответствует периодическая свертка их Фурье-образов. Для сравнения напомним, что произведению периодических Фурье-образов сворачиваемых последовательностей соответствует свертка последовательностей во временной области.
Таким образом, имеем, так называемые соотношения двойственности:
.
Замечание. Соотношение (4.26) используется при проектировании цифровых фильтров методом весовых функций (окон).
4.7. Идеальные частотно-избирательные системы
4.7.1. Импульсная характеристика идеального фильтра нижних частот
Важный класс линейных стационарных систем включает в себя системы, для которых частотная характеристика равна единице над определенным промежутком частот и нулю в остальной области. Такую характеристику имеют идеальные частотно-избирательные фильтры. Например, фильтр нижних частот фильтр, фильтр высоких частот (ФВЧ), полосовой фильтр (ПФ) (резонаторный фильтр), полосно-задерживающий фильтр (режекторный). На рисунке 4.11.а показана комплексная частотная характеристика идеального ФНЧ. а

Рисунок 4.11 – Комплексная частотная характеристика ФНЧ с частотой среза
Поскольку КЧХ полностью определяется своими значениями на полуинтервале , частотную характеристику идеального ФНЧ можно рассматривать только на этом полуинтервале, рисунок 4.11.б.
Вне этого интервала КЧХ повторяется периодично с периодом 2 .
Пример 4.3. Вычислить импульсную характеристику идеального ФНЧ, если его частотная характеристика равная на промежутке [–
,
вне этого интервала вычисляется по периодичности.
Решение. Импульсная характеристика вычисляется с помощью обратного преобразования Фурье
(
|
|
|
|
|
(4.27) |
|
|
|
|
|
|
||
Пусть значение нормированной частоты среза равно |
|
Этой частоте |
||||
|
||||||
соответствует значение линейной частоты |
|
|
||||
Например, если частота дискретизации |
Гц, то |
Гц. |
Область определения аналогового сигнала по частоте составляет |
|
|
Гц. |
|
|
Вычислим несколько значений коэффициентов |
Для |
получаем |
– неопределенность вида Применяя правило Лопиталя, дифференцируем числитель и знаменатель по .
Для других значений |
имеем: |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
; |
|
|
|
|
; |
|
|
|
|
|
; |
; |
|
и |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|||||||||||||
т.д.
На рисунке 4.12 показана импульсная характеристика идеального ФНЧ.
1
0,5
h(n)
0
-6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6
-0,5
n
Рисунок 4.12 – Импульсная характеристика идеального ФНЧ,
(частота среза |
|
) |
|
||
Как видно, члены последовательности |
|
стремятся к нулю при |
неограниченном возрастании , но не быстрее, чем .
5. Проектирование линейных дискретных систем
5.1. Частотно-избирательные цифровые фильтры
В широком понимании фильтром можно назвать систему, меняющую форму исходного сигнала, т.е. меняющую амплитудно-частотную и / или фазо-частотную характеристику сигнала. Результат фильтрации – это измененный спектральный состав сигнала. Например, достигается снижение помех, улучшение или реставрация изображений, извлечение из сигналов
информации, разделение сигналов, сжатие сигнала с целью эффективного использования канала связи, биомедицинская обработка сигнала, цифровое аудио и пр.
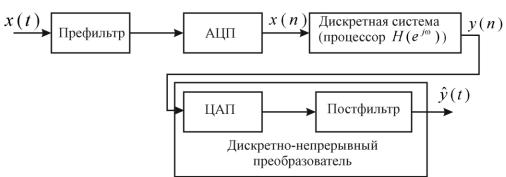
Цифровой фильтр (ЦФ) – это математический алгоритм, реализованный на аппаратном и / или программном уровне. Обобщенная структурная схема цифрового частотно-избирательного фильтра с аналоговым входом и выходом показана на рисунке 5.1.
5.1 – Структурная схема цифрового фильтра
Если дискретная система линейна и стационарна, то
|
|
, |
|
|
где |
– комплексная частотная характеристика системы, или что то же |
|||
самое Фурье-образ ее импульсной характеристики |
, а |
и |
||
Фурье-образы входного и выходного сигналов; |
– отклик дискретной |
|||
системы на входную последовательность |
. |
|
|
|
Проектирование фильтров включает в себя следующие этапы:
–спецификации необходимых свойств требований фильтра, которые зависят от приложений;
–аппроксимаций спецификаций с помощью подходящей структуры дискретная система;
–вычисления импульсной характеристики фильтра;
–анализ влияния разрядности на производительность фильтра;
–реализации цифрового фильтра, которая зависит от используемой технологии на аппаратном и / или программном уровне.
5.1.1.Спецификация требований фильтра
Спецификация требований включает такие основные свойства:
–характеристики сигнала (тип источника и получателя сигнала, интерфейс ввода-вывода, скорость передачи данных, ширина полосы частот сигнала);
–характеристики фильтра (амплитудная и / или фазовая, точность, режимы фильтрации: реальное время или моделирование);
