Метода ЦОС

(2.8)

Из формул (2.6), (2.8) следует, что любой сложный периодический сигнал может быть представлен в виде суммы гармонических колебаний с частотами, кратными основной частоте.

Пример 2.2. Временное представление гармонического колебания имеет следующий вид:

,

или Для представления такого колебания в частотной области достаточно задать

две функции частоты, показывающие, что на частоте амплитуда сигнала равна , а начальная фаза равна :

2.3. Представление дискретных последовательностей

Теория цифровой обработки сигналов связана с описанием и обработкой временных и частотных последовательностей. Пусть задана произвольная временная дискретная последовательность . Такая числовая последовательность может быть представлена как сумма взвешенных и задержанных цифровых единичных импульсов. Цифровой единичный импульс (отсчёт), рисунок 2.4а, определяется следующим образом:

(2.10)

где = 0,

a

б)

1 к

-2 -1 0 1 2 3 4 5

Рисунок 2.4 В цифровых системах этот импульс играет такую же роль, как и дельта-

функция Дирака (рисунок 2.5) в аналоговых системах. По определению δ-функция удовлетворяет следующим условиям:

Рисунок 2.5 – Символическое изображение дельта-функции

Таким образом, δ-функция равна нулю при всех отличных от нуля значениях аргумента и принимает в точке t = 0 бесконечно большое значение. Площадь под кривой, ограниченной δ-функцией, равна единице. Различие между цифровым единичным импульсом и δ-функцией состоит в том, что цифровой единичный импульс является физически реализуемым сигналом, тогда как аналоговый единичный импульс рассматривается только как обобщённая функция. На рисунке 2.4б изображён единичный отсчёт, задержанный на к отсчётов, который определяется как

(2.11)

где = 0, В общем случае любой отсчёт произвольной дискретной последовательности

записывается в виде

(2.12)

x(n)

n

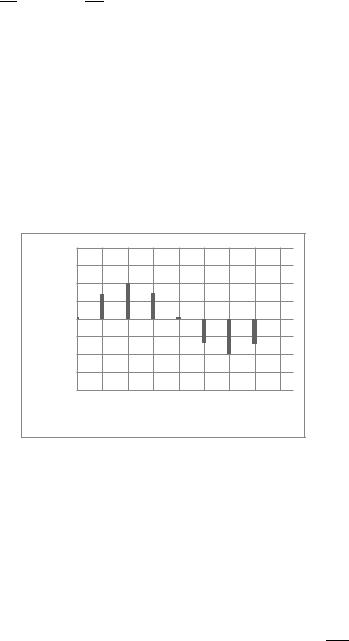
Рисунок 2.6 Значение отсчёта данной последовательности определяется как

Упражнение 2.1. Дана дискретная последовательность

. Записать выражение, определяющее значение отсчёта последовательности с номером n =3.

2.4. Теорема дискретизации

Дискретизация представляет собой процедуру взятия мгновенных значений непрерывного сигнала

Положение 1. Задан сигнал, энергия которого полностью содержится внутри полосы частот от 0 до W Гц; сигнал дискретизируется с интервалами Т секунд.

Теорема 2.1. Исходный сигнал может быть полностью восстановлен при частоте дискретизации не менее 2W.

В западной научной литературе принято считать, что принцип дискретизации был высказан Найквистом (H. Nyqust) в 1928 году. По советским источникам теорему дискретизации сформулировал и доказал академик В. А. Котельников в 1931 году. Строгое определение и использование в качестве теоремы дано Шенноном (C. E .Shannon) в 1948 году.

Положение 2. Задан сигнал (приближенно) с частотным спектром, ограниченным частотой W Гц, существующий t секунд.

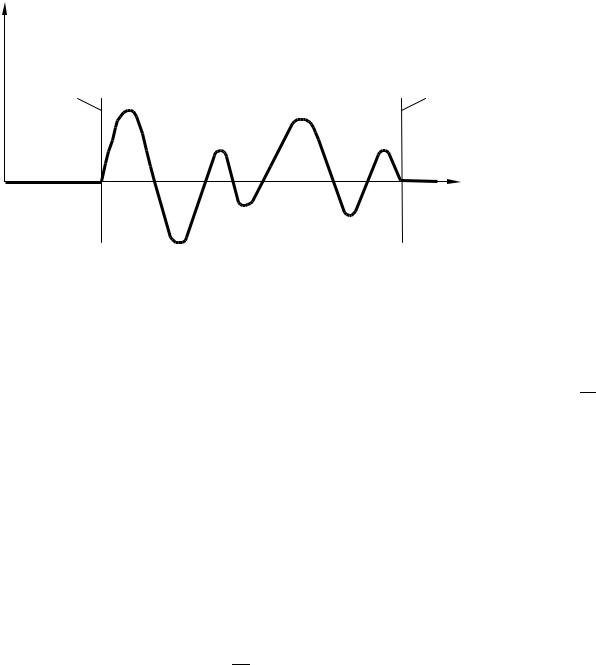
Теорема 2.2. Сигнал может быть полностью восстановлен (описан) отсчётами.

Замечание ‒ Определение сигнала как приближённое введено для математической корректности. По самой природе преобразования Фурье никакая функция не может быть ограничена по частоте. Существует концептуальная трудность строгого частотного ограничения реального

t

Рисунок 2.7 Фактически бесконечность спектра является препятствием для

преобразования сигнала в цифровую форму. Если , дискретизация невозможна. Тем не менее, в спектре любого конечного сигнала есть такие высшие составляющие, значения которых имеют незначительные амплитуды, и потому ими можно пренебречь без заметного

искажения самого сигнала. Ограничение спектра до частоты осуществляется антиэлайсинговым фильтром. Например, для телефонного

, при любых .

На практике широко используется и функция автокорреляции

Функция корреляции описывает важное свойство процесса (сигнала), а именно, изменение отклика на сигнал при изменении временного положения сигнала.

Корреляционная функция ‒ это показатель сходства или общих свойств двух сигналов. Значение 0 указывает на нулевую корреляцию. Это означает, что сигналы независимы, например, если один из сигналов случаен. Малые

изаписывается как

Этот математический аппарат находит очень широкое применение в обработке изображений, в сфере компьютерного зрения, дистанционного зондирования со спутников, в которых сравниваются данные с различных изображений, в реализации технического контроля качества выпускаемых изделий, в климатологии и в др. приложениях.

Стационарный случайный процесс – статистические свойства его не изменяются при переносе начала отсчёта времени (или другого аргумента, от которого зависит рассматриваемый процесс).

Нестационарный процесс – анализ осуществляется лишь по одной реализации процесса. Различают нестационарные процессы с переменным во времени значением, рисунок 2.8а, и с переменным во времени средним квадратом, рисунок 2.8б.

а

t

б

t

Рисунок 2.8

Теоретически точное восстановление сигнала после дискретизации может быть выполнено с помощью идеального ФНЧ с прямоугольной

По теореме дискретизации максимальная частота аналогового сигнала не должна превышать половина частоты дискретизации , следовательно, в частотной области все дискретные сигналы целесообразно рассматривать в

диапазоне ] или .

При анализе дискретных сигналов удобно пользоваться нормированной

частот позволяет исследовать частотные характеристики дискретных систем и спектры дискретных сигналов в единой полосе частот. Для ЦОС важны не абсолютные значения частоты сигнала и частоты дискретизации, а их отношение, т.е. значение нормированной частоты. Покажем это на примере.

Пример 2.4. На рисунке 2.9 изображена дискретная синусоида

x(n)

n

Рисунок 2.9

Она связана с аналоговым гармоническим сигналом выражением

где – период дискретизации.

Сравним две дискретные синусоиды, каждая из которых имеет следующие значения параметров:

где

Действительно, форма этих дискретные сигналы одинакова, так как равны их нормированные частоты, т.е.

.

Пример 2.5. Определить ширину полосы частот цифрового сигнала покомпонентного телевидения (ТВ).

Замечание. В покомпонентном телевидении разделённые сигналы

строчном интервале ТВ стандарта c параметрами: 625 строк в кадре, 25 полукадров в секунду. Частота дискретизации сигнала яркостного канала

секунду. Частота дискретизации сигнала цветности .

2.3. Определить скорость цифрового потока полного сигнала цветности ТВ изображения при 8-битовом квантовании и стандарте цифрового кодирования 4:2:2. Условие 4:2:2 отражает соотношение частот дискретизации сигнала яркости и двух цветоразностных сигналов, а также одновременность их передачи.

2.4. Количество отсчётов HD телевизионного изображения равно

. Число градаций яркости равно 256. Какой объем памяти требуется для хранения этого изображения.

3. Линейные системы

3.1. Преобразование сигналов линейными системами с постоянными параметрами

Анализ физической системы, использующей технику обработки сигналов, часто приводит к схеме, которая представлена на рисунке 3.1.

Линейность системы означает, что входному сигналу вида

будет соответствовать сигнал на выходе системы

.

Одна из проблем анализа линейной системы заключается в том, как выяснить особенности системы, если возможно измерить сигналы на входе и сигналы на выходе. Чтобы решить эту задачу, необходимо знать, как связаны входной и выходной сигналы с параметрами системы.

3.1.1. Дискретные системы

Дискретная система определяется как однозначное преобразование или оператор, переводящий входную последовательность (вход) в выходную (выход, отклик, или реакция системы). Математически это записывается в виде

и графически изображается на рисунке 3.2.

Линейная

система

Рисунок 3.2 ‒ Дискретная система

Соотношение (3.1) ‒ это правило, или формула, по которому вычисляется реакция системы через отсчеты сигнала, поданного на ее вход. Вид оператора

Пример 3.1. Дискретная система, описываемая формулой

(3.2)

где ‒ натуральное число, называемое задержкой системы. Эта система осуществляет сдвиг входной последовательности отсчетов вправо на интервалов дискретизации. Для вычисления отсчета отклика используется единственный отсчет входной последовательности. Говорят, что система (3.2) имеет память и относится к системам с запоминанием.

3.2. Линейные дискретные системы с постоянными параметрами

Во многих приложениях применяется класс линейных систем с постоянными параметрами. Они сравнительно просты в математическом отношении, дают удобный вид обработки сигналов. Класс линейных систем определяется

Выражение (3.3) характеризует свойство аддитивности линейной системы, в соответствии с которым реакция системы на сумму воздействий равна сумме реакций на каждое воздействие. Выражение (3.3) характеризует также свойство однородности линейной системы, в соответствии с которым умножение входной последовательности на постоянный параметр соответствует выходной последовательности, умноженной на тот же параметр, т.е.

систему, то это означает, что в данном преобразовании (отображении) возможны только линейные операции сложения, вычитания и умножения на