
- •Дискретное преобразование Уолша-Адамара
- •Дискретное косинусное преобразование
- •Дискретное преобразование Хартли
- •5. Теорема о корреляции. По определению (2.13) корреляционная функция двух конечных последовательностей равна
- •6. Теорема Парсеваля. Пусть последовательности и будут идентичными. В этом случае теорема о корреляции записывается как
Дискретное преобразование Хартли
К линейному ортогональному преобразованию относится и преобразование Хартли (ПХ). Это преобразование связано с преобразованием Фурье, результат выражается действительными числами, но в отличии от косинусного прямое и обратное преобразования Хартли совпадают, что может обеспечить экономию аппаратных средств. [1]
Прямое и обратное одномерное ПХ записывается следующим образом:
|
|
(27) |
|
|
(28) |
где cas( )
= cos(
)
= cos(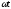 )+sin(
)+sin(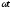 );
);
 - круговая частота;
- круговая частота;
t – время.
Дискретное одномерное преобразование Хартли (ДПХ) имеет вид
|
|
(29)
|
где
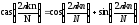 .
.
Выражение (29) задает
коэффициенты разложения (коэффициенты
Хартли) некоторой действительной функции
g(n)
по дискретным функциям
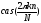 ,
причем g(n)
задана на дискретном множестве аргументов
n
,
причем g(n)
задана на дискретном множестве аргументов
n {0,1,…,N-1}.
{0,1,…,N-1}.
Используя свойство ортогональности функций, можно получить выражение для обратного одномерного дискретного преобразования Хартли (ОДПХ):
|
g(n)= |
(30) |
Матричная форма записи одномерного прямого ДПХ имеет вид
|
[G(k)]=[v(k,n)][g(n)],
k, n |
(31)
|
где [v(k,n)]= - матрица дискретного множества
ортогональных функций ДПХ размером
(N
- матрица дискретного множества
ортогональных функций ДПХ размером
(N N);
N);
[G(k)]
– вектор-столбец спектральных
коэффициентов ДПХ размером (N 1);
1);
[g(n)] – вектор-столбец дискретных значений (отсчетов) сигнала.
Обратное одномерное ДПХ в матричной форме записи представляется как:
|
[g(n)]= |
(32)
|
Прямое ДПХ
двухмерного фрагмента изображения
размером (N N)
запишется в виде
N)
запишется в виде
|
[G( |
(33)
|
где [g( )]
– сигнальная матрица размером (N
)]
– сигнальная матрица размером (N N);
N);
[G( )]
– матрица спектральных коэффициентов
ДПХ размером (N
)]
– матрица спектральных коэффициентов
ДПХ размером (N N);
N);
[v(k,n)]
– квадратная матрица ДПХ размером
(N N):
N):
|
|
(34) |
Двухмерное обратное преобразование Хартли записывается в виде
|
[g( |
(35) |
Отметим, что матрицы
преобразований прямого и обратного ДПХ
идентичны, так как [v(k,n)]=[v(k,n)]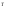 [10].
[10].
Быстрое преобразование Фурье
Существует два класса алгоритмов вычисления преобразования Фурье обычное дискретное преобразование Фурье и быстрое дискретное преобразование Фурье (БПФ). Быстрый алгоритм позволяет эффективно вычислять ДПФ. При этом сокращается количество выполняемых арифметических операций, а также объем памяти, необходимый для вычисления ДПФ. В результате многие задачи спектрального анализа, обработки сигналов за счет уменьшения вычислительной сложности решаются в реальном времени.
5.1. Вычислительная сложность дискретного преобразования Фурье
Рассмотрим матричную форму ДПФ (4.25), (4.26):
– прямое
ДПФ
 ,
,
– обратное
ДПФ
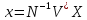 .
.
Если
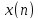 – комплекснозначная последовательность,
то для вычисления одного коэффициента
ДПФ потребуется выполнить
– комплекснозначная последовательность,
то для вычисления одного коэффициента
ДПФ потребуется выполнить
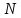 умножений и
умножений и
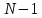 сложений комплексных чисел, т.е. сложность
оценивается как
сложений комплексных чисел, т.е. сложность
оценивается как
комплексных
умножений
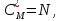
комплексных
сложений
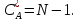
4.4.4. Свойства дискретного преобразования Фурье
1.
Периодичность. Свойство периодичности
ДЭФ
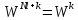 приводит к выражениям
приводит к выражениям

Действительно,
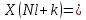
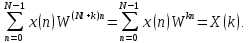
Обычно
ограничиваются рассмотрением одного
периода длиной
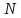 во временной и в частотной области. Это
позволяет определить матричную форму
ДПФ:
во временной и в частотной области. Это
позволяет определить матричную форму
ДПФ:
– прямое
ДПФ
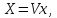 (4.25)
(4.25)
где
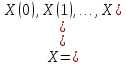 и
и
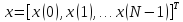 –
векторы
–
векторы
отсчетов последовательности спектральных коэффициентов и сигнала соответственно;
– обратное
ДПФ
 .
Используя формулу (4.20), получаем
.
Используя формулу (4.20), получаем
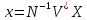 .
(4.26)
.
(4.26)
2.
Линейность. Класс
линейных систем определяется линейными
операциями или принципом суперпозиции.
Если
 и
и
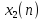 входные последовательности, а
входные последовательности, а
 и
и
 соответственно их ДПФ,
то при подаче на вход последовательности
соответственно их ДПФ,
то при подаче на вход последовательности
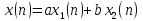 систему называют линейной тогда и только
тогда, когда выполняется
систему называют линейной тогда и только
тогда, когда выполняется

где
 и
и
 произвольные постоянные параметры
(константы). Спектр последовательности
произвольные постоянные параметры
(константы). Спектр последовательности
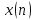 равен
равен
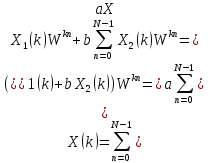

3. Инвариантность ДПФ относительно сдвига по времени и частоте:
1.
Инвариантность относительно циклического
сдвига по времени. Если последовательность
 имеет ДПФ
имеет ДПФ
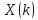 ,
то ДПФ последовательности
,
то ДПФ последовательности
 равно
равно
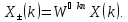
Рассмотрим
две последовательности
 и
и
 .
Формы последовательности показаны на
рисунке 4.6.а,б.
.
Формы последовательности показаны на
рисунке 4.6.а,б.
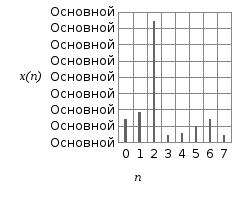

Рисунок 4.6
ДПФ
последовательности
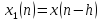 равно
равно
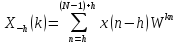 .
.
Заменяя
индекс суммирования
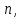 и введя новую переменную
и введя новую переменную
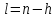 ,
получим
,
получим
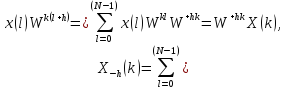
где
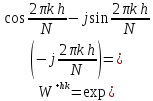 ).
Тогда
).
Тогда
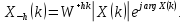
Таким образом, при сдвиге дискретного сигнала по времени изменениям подвергаются только фазы дискретных функций (фазовый спектр), амплитудный спектр не изменяется.
2.
Инвариантность относительно сдвига по
частоте. Если спектральной последовательности
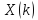 соответствует последовательность
соответствует последовательность
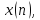 то при сдвиге последовательности
то при сдвиге последовательности
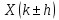 исходная последовательность
исходная последовательность
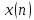 получит фазовый сдвиг, т.е.
получит фазовый сдвиг, т.е.

Пусть
 Обратное ДПФ
последовательности
Обратное ДПФ
последовательности
 равно
равно
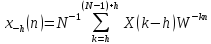 .
.
Заменяя
индекс суммирования
 ,
и введя новую переменную
,
и введя новую переменную
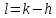 ,
получим
,
получим
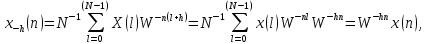
где
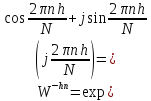 ).
).
4.
Теорема о свертке. Если исходные
последовательности отсчетов сигналов
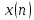 и
и
 имеют конечные периоды
имеют конечные периоды
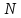 ,
их циклическая свертка определяется
формулой
,
их циклическая свертка определяется
формулой
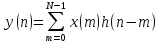 ,
𝑛
= 0, 1,…, 𝑁–1.
,
𝑛
= 0, 1,…, 𝑁–1.
Вычислим
ДПФ последовательности

 (4.27)
(4.27)
Так
как
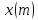 не зависит от
не зависит от
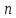 ,
изменяем порядок суммирования в (4.27).
,
изменяем порядок суммирования в (4.27).
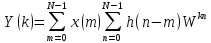 .
(4.28)
.
(4.28)
Используя свойство инвариантности относительно циклического сдвига по времени, можно записать составляющую выражения (4.28) как
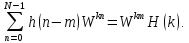
Тогда
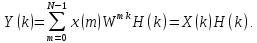 (4.29)
(4.29)
Таким образом, спектр свертки равен произведению спектров сворачиваемых последовательностей. Коэффициенты свертки вычисляются на основе ОДПФ по формуле
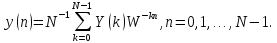
Теорема (4.29) позволяет вычислить коэффициенты свертки при помощи ДПФ по формуле
 .
.
При больших величинах 𝑁 на практике применяют эффективные алгоритмы вычисления свертки с использованием быстрых преобразований Фурье.

 ,
,
 ,
,
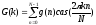 ,
k
,
k {0,1,…,N-1},
{0,1,…,N-1},
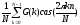 ,
n
,
n {0,1,…,N-1},
{0,1,…,N-1},
 {0,1,…,N-1},
{0,1,…,N-1},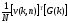 ,
k, n
,
k, n {0,1,…,N-1},
{0,1,…,N-1},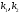 )]
)]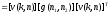 ,
,
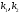 ,
,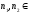 {0,1,…,N-1},
{0,1,…,N-1},
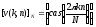 ,
k, n
,
k, n {0,1,…,N-1},
{0,1,…,N-1},
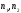 )]=
)]=
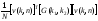 .
.