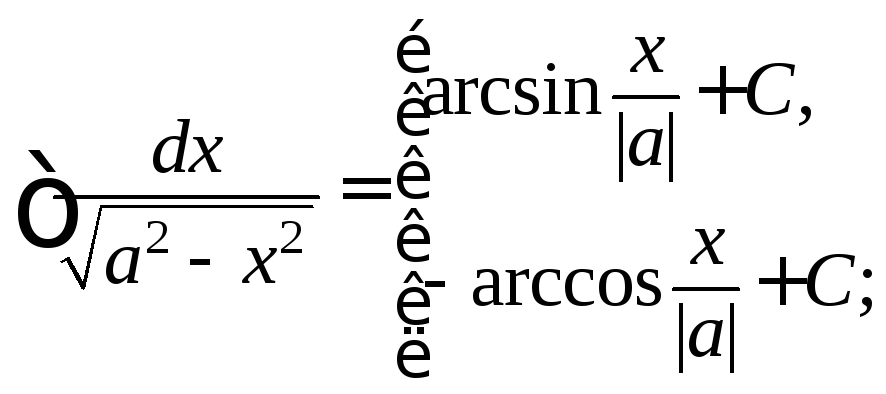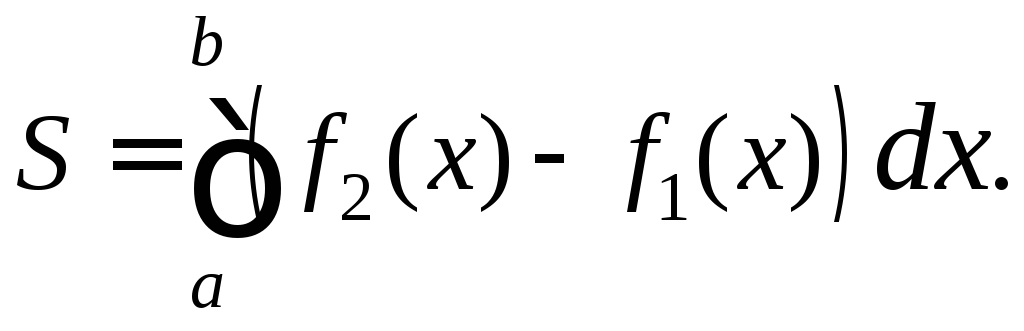3.3. Краткие теоретические сведения к выполнению контрольных работ

Задания 1 – 10. Алгебраическая форма комплексного числа:

где

Если то:

Числу на координатной плоскости соответствует точка

Расстояние d между точками ив прямоугольной декартовой системе координат:

Всякое комплексное число можно представить втригонометрической форме

или в показательной форме

где –модуль числа z;

либо –аргумент числа z:

Если причемто:

Если причемто:

Задания 11 – 20. Если то

Корень n-й степени из комплексного числа z имеет n различных значений.

Задания 21 – 30. Система трех линейных алгебраических уравнений с тремя неизвестными имеет вид

где – коэффициенты системы;– свободные члены.

Матрица

называется матрицей системы.

–матрица-столбец неизвестных; – матрица-столбец свободных членов.

Определитель

называется определителем системы.

Матрица

называется расширенной матрицей системы.

Элементарными преобразованиями строк матрицы называются:

1) перестановка строк;

2) умножение строки на одно и то же число λ

) прибавление к строке матрицы другой ее строки, умноженной на некоторое число.

Если определитель системы то система имеет единственное решение.

Метод Крамера. Необходимо:

1) вычислить определитель Δ;

2) в определителе Δ заменить поочередно i-й столбец столбцом свободных членов и вычислить соответствующие определители

3) вычислить значения поформулам Крамера:

4) записать решение

Метод обратной матрицы. Необходимо:

1) записать систему в матричном виде:

где A – матрица системы;

X – матрица-столбец неизвестных;

B – матрица-столбец свободных членов;

2) решить матричное уравнение

где – обратная матрица;

3) записать решение

Метод Гаусса. Необходимо:

1) записать расширенную матрицу системы;

2) с помощью элементарных преобразований строк расширенной матрицы свести матрицу системы к треугольной или трапециевидной (с нулевыми элементами под главной диагональю);

3) для преобразованной таким образом расширенной матрицы записать соответствующую систему уравнений;

4) решить полученную систему, начиная с последнего уравнения;

5) записать решение

Задания 31 – 40. Базисом в пространстве называются три упорядоченных некомпланарных вектора.

Векторы называются компланарными, если они параллельны одной и той же плоскости. Для компланарности ненулевых векторов необходимо и достаточно, чтобы их смешанное произведение было равно нулю, т. е.

Если то смешанное произведение в координатной форме:

Упорядоченная тройка некомпланарных векторов с общим началом называетсяправой, если кратчайший поворот от вектора к векторунаблюдается из конца вектораи происходит против хода часовой стрелки. В противном случае тройка векторов называетсялевой.

Тройка векторов является правой тогда и только тогда, когдаи левой, когда

Задания 41 – 50. Пусть Тогда

Площадь S треугольника, построенного на векторах

где – длина вектора и

Объем V пирамиды, построенной на векторах

где – модуль числа и

Уравнение прямой, проходящей через точки и

Уравнение плоскости, проходящей через точки и

Задания 51 – 60. На плоскости уравнение

задает эллипс с полуосями a, b и центром в точке в пространстве – эллиптический цилиндр.

На плоскости уравнение

задает гиперболу с полуосями a, b и центром в точке в пространстве – гиперболический цилиндр.

На плоскости уравнения

или

задают параболы с осью симметрии, параллельной одной из координатных осей, и вершиной в точке в пространстве – параболические цилиндры.

Задания 61 – 70. Последовательность, имеющая предел, называется сходящейся, в противном случае – расходящейся.

Если последовательности и сходятся, то:

Выражения вида называютсянеопределенностями.

При раскрытии неопределенности вида используют формулу

где – иррациональное число.

Задания 71 – 80. Правила дифференцирования. Если – дифференцируемые функции, то:

Если – сложная функция, где– дифференцируемые функции, то

Таблица производных.

в частности,

в частности,

в частности,

Задания 81 – 90. Если существуют ито:

При раскрытии неопределенности вида часто используют формулы:

(первый замечательный предел);

Функция называетсябесконечно малой при если

Если гдеи– бесконечно малые притоиназываютсяэквивалентными; пишут:

Если отношение двух бесконечно малых имеет предел, то он не изменится при замене каждой из бесконечно малых эквивалентной ей бесконечно малой.

Если прито верны следующие эквивалентности:

Правило Лопиталя. Если и– непрерывные функции, имеющие производные в проколотой окрестности точкипричемв указанной окрестности,(илии существуетто

Задания 91 – 100. При вычислении частной производной функции трехпеременных считаютy, z постоянными и пользуются правилами дифференцирования и таблицей производных для функции одной переменной x.

При вычислении частной производной считают, чтоy – переменная величина, x, z – постоянные, дифференцируют как функцию переменной y; при вычислении частной производной считают, чтоz – переменная величина, x, y – постоянные, дифференцируют как функцию переменной z.

Если вектор имеет направляющие косинусыто производную функциив точкепо направлению векторанаходят по формуле

Градиентом функции в точкеназывается вектор

Задания 101 – 110. Частными производными второго порядка функции называются частные производные от ее частных производных первого порядка:

Аналогично определяются частные производные третьего, четвертого и высших порядков от функции трех и более переменных.

Смешанной частной производной называется частная производная второго порядка и выше, взятая по различным переменным.

Если частные производные высшего порядка непрерывны, то смешанные производные одного порядка не зависят от порядка дифференцирования.

Задания 111 – 120. Правила интегрирования.

Таблица интегралов.

в частности,

Метод непосредственного интегрирования основан на использовании только основных свойств неопределенного интеграла и таблицы интегралов.

Метод замены переменной (или метод подстановки) используют в двух случаях:

а)

где – первообразная для

б)

где – первообразная для

При использовании метода поднесения под знак дифференциала замену переменной не применяют. Интеграл вычисляют по формуле

где – первообразная для

Интегрированием по частям называется вычисление интеграла по формуле

где – дифференцируемые функции.

Для нахождения интегралов

где – многочлен,

за u принимают многочлен а за– выражения соответственно

Задания 121 – 130. Для вычисления определенного интеграла используют формулу Ньютона-Лейбница

где – первообразная функция для

При использовании метода замены переменной (или метода подстановки) определенный интеграл вычисляют по формуле

При нахождении определенного интеграла с помощью метода интегрирования по частям используют формулу

где – функции, дифференцируемые на

Неопределенный интеграл вида

где R – рациональная функция,

выделением полного квадрата сводится к одному из трех типов интегралов:

для вычисления которых используют соответственно следующие тригонометрические подстановки:

Задания 131 – 140. Площадь плоской фигуры, ограниченной кривыми и прямыминаходится по формуле

Задания 141 – 150. Дифференциальное уравнение вида

называется уравнением с разделяющимися переменными.

Предполагая, что почленным делением наего сводят к уравнению

Далее равенство интегрируют и получают общий интеграл.

Дифференциальное уравнение вида

называется однородным, если обе функции являются однородными функциями одной и той же степениn, т. е. при любом выполняются условия:

Однородное уравнение может быть приведено к виду

Для решения однородного уравнения делают замену где т. е. и сводят его к уравнению с разделяющимися переменными.

Линейное однородное дифференциальное уравнение n-го порядка с постоянными коэффициентами имеет вид

где

Общим решением этого уравнения является функция

где …,–линейно независимые частные решения;

–произвольные постоянные.

Для нахождения частных решений данного уравнения составляют характеристическое уравнение

и решают его.

Каждому корню характеристического уравнения соответствует определенное частное решение:

а) если – простой действительный корень, то ему соответствует решение вида

б) если – действительный корень кратностьюk то ему соответствуетk частных решений

…,

в) если – пара комплексно-сопряженных корней, то им соответствуют два частных решения:

г) если – пара комплексно-сопряженных корней кратностьюk то им соответствуютчастных решения:

…,

…,

Задания 151 – 160. Дифференциальное уравнение вида

где – заданные непрерывные функции,

называется линейным дифференциальным уравнением первого порядка.

Метод Бернулли. Для решения линейного дифференциального уравнения первого порядка необходимо:

1) искать общее решение уравнения в виде где– функции, которые надо найти;

2) подставить в заданное уравнение;

3) записать уравнение в виде

4) найти функцию как частное решение дифференциального уравнения

5) найти общее решение уравнения

6) записать общее решение исходного уравнения для найденных функцийu, v.

Задачей Коши для дифференциального уравнения первого порядка называется задача нахождения частного решения дифференциального уравнения, удовлетворяющего заданному начальному условию

Задания 161 – 170. Объем V цилиндрического тела T, ограниченного сверху поверхностью снизу плоскостьюи сбоку цилиндрической поверхностью, вычисляют по формулам: где область D – проекция тела на плоскости

Если то

Если то

Если то

Задания 171 – 180. Потоком вектора через поверхность σ называется поверхностный интеграл по поверхности σ от скалярного произведения вектора поля и единичного векторанормали к поверхности:

Если поверхность σ является замкнутой, то пишут:

причем за направление вектора берут направление внешней нормали.

Формула Остроградского – Гаусса:

где – дивергенция векторного поля.

Если переменные x, y, z в тройном интеграле заменяют цилиндрическими координатами

то используют формулу

где T* – область в цилиндрической системе координат, соответствующая области T в декартовой системе координат.

Циркуляцией векторного поля вдоль замкнутого контураL называется криволинейный интеграл

где – единичный вектор, направленный по касательной к кривойL в направлении ее обхода.

Положительным направлением обхода замкнутого контура называется направление, при котором линия интегрирования обходится против хода часовой стрелки, а отрицательным – по ходу часовой стрелки.

Если кривая L задана параметрически в пространстве уравнениями гдето

Задания 181 – 190. Числовым рядом называется выражение вида

где

Сумма

называется n-й частичной суммой.

Если существует предел

то ряд называется сходящимся, а S – его суммой; пишут:

Если не существует, то ряд называетсярасходящимся.

Необходимый признак сходимости. Если ряд сходится, то

Следствие необходимого признака сходимости. Если то ряд расходится.

Признак сравнения. Пусть для знакоположительных рядов иначиная с некоторогоn выполняется неравенство

Тогда:

а) из сходимости ряда следует сходимость ряда

б) из расходимости ряда следует расходимость ряда

Предельный признак сравнения. Если для знакоположительных рядов исуществует

то оба эти ряда сходятся или оба расходятся.

Для исследования по признаку сравнения или предельному признаку сравнения часто используют следующие ряды:

а) ряд сходящийся прии расходящийся при

б) ряд Дирихле сходящийся прии расходящийся при

Предельный признак Д’Аламбера. Пусть для знакоположительного ряда существует

Тогда:

а) при ряд сходится;

б) при ряд расходится.

Предельный признак Коши. Пусть для знакоположительного ряда существует

Тогда:

а) при ряд сходится;

б) при ряд расходится.

Если в предельных признаках Д’Аламбера и Коши получаем то нужны дополнительные исследования по другим признакам.

При использовании предельного признака Коши часто применяют формулу

Иинтегральный критерий сходимости. Пусть члены ряда имеют видгде– неотрицательная монотонно убывающая нафункция. Ряд сходится (расходится) тогда и только тогда, когда сходится (расходится) несобственный интеграл

Задания 191 – 200. Знакопеременный числовой ряд называетсяабсолютно сходящимся, если сходится ряд

Абсолютно сходящийся ряд сходится.

Знакопеременный ряд называется условно сходящимся, если он сходится, но не абсолютно.

Знакопеременный ряд называется знакочередующимся, если любые два его соседних члена имеют разные знаки:

где

Признак Лейбница. Если для знакочередующегося ряда выполняются условия:

1) 

2) 

то ряд сходится.

Следствие признака Лейбница. Если –n-я частичная сумма знакочередующегося ряда то

Степенным рядом называется ряд вида

где

Радиусом сходимости степенного ряда называется число r, которое находят по формулам:

или

Ряд сходится, причем абсолютно, наинтервале сходимости гдеи расходится на

Для определения области сходимости степенного ряда следует:

1) найти его радиус сходимости;

2) определить интервал сходимости с центром в точке a;

3) выяснить вопрос о сходимости ряда в граничных точках этого интервала, подставив их вместо x в заданный ряд.

Задания 201 – 210. Степенной ряд вида

называется рядом Тейлора функции

Рядом Маклорена функции называется ряд Тейлора вида

Имеют место разложения элементарных функций в ряд Маклорена:

Задания 211 – 220. Рядом Фурье -периодической функции называется функциональный ряд вида

где коэффициенты вычисляют по формулам:

Теорема Дирихле. Пусть -периодическая функцияявляется кусочно-гладкой наТогда ее ряд Фурье сходится кв каждой точкенепрерывности и к в точке разрыва, гдеи– соответственно левосторонний и правосторонний пределы функции в точкеx.

Задания 221 – 230. Рядом Лорана функции называется ряд вида

где

Ряд называемыйправильной частью ряда Лорана, сходится в круге Рядназываемыйглавной частью ряда Лорана, сходится вне круга

Функция аналитическая в кольцеразлагается в этом кольце в абсолютно сходящийся ряд Лорана

Имеет место разложение:

Задания 231 – 240. Функция называется аналитической в точке, если существует некоторая окрестность этой точки, в которой функция однозначна и дифференцируема. Функция называетсяаналитической в области D, если она аналитическая в каждой точке этой области.

Изолированной особой точкой функции называется точка, в некоторой проколотой окрестности которой функцияаналитична, но не аналитична в самой этой точке (или не определена в ней).

Изолированная особая точка a функции называетсяустранимой, если ряд Лорана функции имеет вид

Тогда

Изолированная особая точка a функции называетсяполюсом k-го порядка, если

где Тогда

При полюс называютпростым полюсом.

Изолированная особая точка a функции называетсясущественно особой, если

и бесконечное количество элементов отлично от нуля. Тогдане существует.

Вычетом функции в особой точкеa называется коэффициент при первой отрицательной степени ряда Лорана функции в проколотой окрестности точкиa. Пишут:

Если a – простой полюс, то

Если a – полюс k-го порядка, то

Основная теорема о вычетах. Если функция – аналитическая в односвязной областиD, кроме конечного числа особых точек, Γ – замкнутая положительно ориентированная кривая, расположенная в D и содержащая внутри себя особые точки то

Задания 241 – 250. Свойство линейности. Если то

Теорема подобия. Если то

Теорема смещения. Если то

Таблица основных операционных соотношений.

	при		при
	1

Учебное издание