
- •Идз №7:
- •1. Обыкновенные дифференциальные уравнения. Основные понятия
- •2. Дифференциальные уравнения первого порядка
- •2.1. Дифференциальные уравнения с разделяющимися переменными
- •2.2. Однородные дифференциальные уравнения первого порядка
- •2.3. Линейные дифференциальные уравнения первого порядка. Уравнения Бернулли
- •I. Дифференциальное уравнение вида
- •II. Дифференциальное уравнение вида
- •1) И 2).
- •1) И 2) .
- •1) И 2).
- •1) И 2).
- •2.4. Уравнения в полных дифференциалах
- •3. Дифференциальные уравнения второго порядка
- •3.1. Дифференциальные уравнения второго порядка, допускающие понижение порядка
- •4. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •5. Литература
- •Вариант № 1
II. Дифференциальное уравнение вида
![]()
где
m
– любое действительное число, отличное
от нуля и единицы, т.е.
![]() и
и![]() ,
называетсяуравнением
Бернулли.
,
называетсяуравнением
Бернулли.
Уравнение
Бернулли можно преобразовать в линейное
уравнение, производя замену неизвестной
функции при помощи подстановки
![]() .
На практике уравнение Бернулли решается
аналогично тому, как решаются линейные
дифференциальные уравнения первого
порядка, т.е. применяется либо метод
Бернулли, либо метод вариации произвольных
постоянных.
.
На практике уравнение Бернулли решается
аналогично тому, как решаются линейные
дифференциальные уравнения первого
порядка, т.е. применяется либо метод
Бернулли, либо метод вариации произвольных
постоянных.
Пример. Найти общее решением дифференциального уравнения
![]() .
.
Решение.
Имеем уравнение Бернулли. Решим его
методом подстановки (методом Бернулли):
![]() ,
,![]()
![]() ,
,
![]() .
.
Отсюда получаем два уравнения с разделяющимися переменными:
1) И 2).
Решая первое уравнение, находим v как простейший частный интеграл этого уравнения:
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
Таким
образом,
![]() .
.
Подставляя v во второе уравнение и решая его, находим u как общий интеграл этого уравнения:
![]() ,
,
![]() ,
, ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() .
.
Таким
образом,
![]() .
.
Следовательно, искомый общий интеграл данного уравнения
![]() .
.
Ответ:
общее решение уравнения Бернулли
![]() .
.
В задании 3 необходимо найти решение задачи Коши линейного дифференциального уравнения первого порядка.
Задание 3. Найти решение задачи Коши для дифференциального уравнения. Сделать проверку.
a)
![]() .
.
b)
![]() .
.
c)
![]() .
.
Решение. Для нахождения частного решения, или решения задачи Коши предварительно найдем общее решение, а затем, подставляя начальные условия, вычислим соответствующее этим начальным значениям C. Подставляя его в общее решение, получим решение задачи Коши.
Данные уравнения относятся к линейным уравнениям первого порядка. Их можно решать или методом подстановки (метод Бернулли), или методом вариации произвольных постоянных (метод Лагранжа). Для задания 3 (a) покажем оба способа решения, остальные примеры решим только методом Лагранжа.
Задание
3a.
![]() .
.
Первый способ – метод подстановки.
Полагаем
![]() ,
тогда
,
тогда![]() и данное уравнение преобразуется к
виду:
и данное уравнение преобразуется к
виду:
![]() ,
,
![]() .
.
Так
как одну из вспомогательных функций uилиv можно взять
произвольно, то выберем в качествеvкакой-либо частный интеграл уравнения![]() .
Тогда для отысканияuполучим уравнение
.
Тогда для отысканияuполучим уравнение![]() .
Таким образом, приходим к двум уравнениям
первого порядка с разделяющимися
переменными:
.
Таким образом, приходим к двум уравнениям
первого порядка с разделяющимися
переменными:
1) И 2) .
Решая первое из этих уравнений, найдем v, как простейший, отличный от нуля частный интеграл этого уравнения:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
Подставляя v во второе уравнение и решая его, находим u как общий интеграл этого уравнения:
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
Интеграл, стоящий слева, вычислим отдельно.
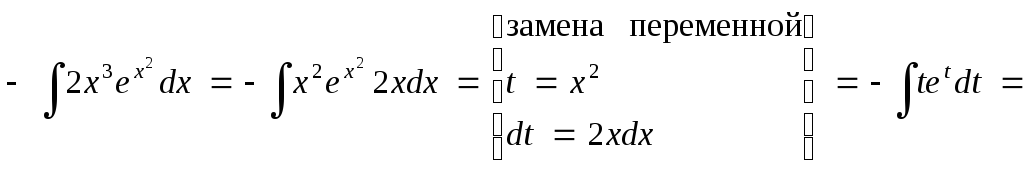
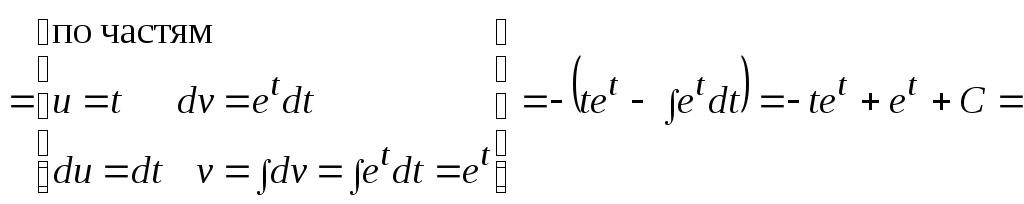
![]()
Возвращаясь к уравнению, получим
![]()
Зная u и v, находим искомую функцию y:
![]()
Таким образом, общее решение исходного уравнения имеет вид:
![]()
Подставим
заданные начальные условия
![]() ,
т.е.
,
т.е.![]() ,
,![]() ,
в общее решение и найдемC:
,
в общее решение и найдемC:
![]() ,
,
![]() ,
,![]() .
.
Таким
образом,
![]() и частное решение, или решение задачи
Коши примет вид:
и частное решение, или решение задачи
Коши примет вид:
![]()
Сделаем проверку.
![]() .
.
Найдем
производную и подставим в исходное
уравнение
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
Получили верное равенство, т.е. решение дифференциального уравнения найдено верно.
Второй способ – метод вариации произвольных постоянных.
1. Составим однородное линейное уравнение, соответствующее исходному уравнению, заменив правую часть уравнения на ноль:
![]()
Полученное уравнение является уравнением с разделяющимися переменными. Решая его, получим
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() .
.
2.
Общее решение исходного неоднородного
уравнения будем искать в виде общего
решения однородного уравнения, считая
C
функцией от x
(![]() ),
то есть
),
то есть![]() .
Подставим это решение в исходное
уравнение и найдем из него неизвестную
функцию
.
Подставим это решение в исходное
уравнение и найдем из него неизвестную
функцию![]() .
.
![]() ,
,
![]() .
.
![]() .
.
![]() .
.
Получили
уравнение первого порядка с разделяющимися
переменными. Разделяя переменные и
интегрируя уравнение (как это было
выполнено при решении уравнения
![]() или
или![]() первым способом с той разницей, что в
первом способе в качестве искомой
функции выступала функция
первым способом с той разницей, что в
первом способе в качестве искомой
функции выступала функция![]() ,
а в нашем случае в качестве искомой
функции выступает функция
,
а в нашем случае в качестве искомой
функции выступает функция![]() ),
получим
),
получим
![]()
Тогда общее решение примет вид
![]() .
.
Как легко заметить общее решение исходного уравнения получились одинаковыми. Частное решение находится аналогично тому, как это было сделано в первом способе.
Задание
3b.
![]() .
.
Разделим
обе части равенства на
![]()
![]()
Полученное
уравнение является обыкновенным линейным
дифференциальным уравнением первого
порядка. Решим его методом подстановки
(методом Бернулли). Полагаем
![]() ,
тогда
,
тогда![]() и данное уравнение преобразуется к
виду.
и данное уравнение преобразуется к
виду.
![]() ,
,
![]()
Отсюда получаем два уравнения с разделяющимися переменными:
