2.2. Однородные дифференциальные уравнения первого порядка

Дифференциальное уравнение первого порядка

(9)

называется однородным относительно переменных x и y, если – однородная функция нулевой степени относительно своих аргументов.

Дифференциальное уравнение первого порядка

(10)

называется однородным относительно переменных x и y, если и– однородные функции одной и той же степениk относительно своих аргументов.

Функция называетсяоднородной степени k относительно переменных x и y, если для произвольного действительного числа a выполняется равенство

.

Однородное дифференциальное уравнение первого порядка (как уравнение (9), так и уравнение (10)) может быть представлено в виде

. (11)

Метод интегрирования однородных дифференциальных уравнений состоит в следующем. Однородное дифференциальное уравнение приводится к виду (11). Вводится новая переменная или, где(), и после подстановки в уравнение (11) приходим к уравнению с разделяющимися переменными относительно переменнойxи новой функцииt(x).

В задании 2 необходимо решить однородное обыкновенное дифференциальное уравнение первого порядка.

Задание 2. Найти общий интеграл (общее решение) дифференциального уравнения. Сделать проверку.

a) , b),

c) , d).

Решение: Во всех случаях имеем однородные относительно переменных x и y обыкновенные дифференциальные уравнения первого порядка. Все они могут быть сведены к уравнению вида (11). В случаях a), c), d) предварительно необходимо показать, что эти уравнения являются однородными, а затем привести их к виду (11).

Задание 2a. .

Данное уравнением является уравнением первого порядка. Рассмотрим функцию . Эта функция является однородной функцией нулевой степени, так как для произвольного действительного числаa выполняется равенство

.

Таким образом, данное уравнением является однородным и его можно свести к уравнению (11). Для этого разделим числитель и знаменатель правой части на x:

; .

Сделаем замену переменной или, где. Найдеми подставим в преобразованное уравнение

; ;;

; .

Пришли к уравнению первого порядка с разделяющимися переменными относительно переменной x и новой искомой функции t(x). Заменяя и разделяя переменные, получим

; .

Проинтегрируем обе части полученного уравнения

Возвращаясь к исходному уравнению, получим

.

Умножив обе части равенства на два и уединяя произвольную постоянную, получим общий интеграл уравнения с разделяющимися переменными

.

Для нахождения общего интеграла исходного уравнения вернемся к старой переменной через замену :

,

,

,

.

Таким образом, общий интеграл исходного уравнения примет вид:

.

Сделаем проверку. Вычислим производную искомой функции как функции, заданной неявно.

, ,

, ,

; ,

, ,.

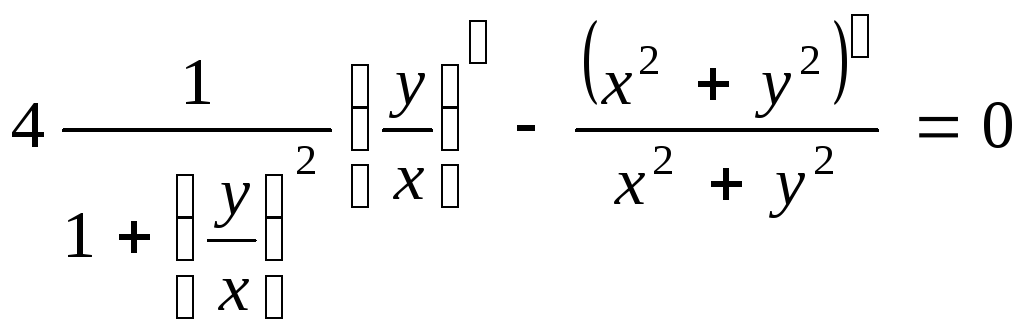Подставим найденное значение в искомое уравнение

и получим тождество (верное равенство).

Ответ: общий интеграл

Задание 2b. .

Имеем обыкновенное дифференциальное уравнение первого порядка, однородное относительно переменных x и y. Сделаем замену переменной или, где. Найдеми подставим в исходное уравнение

; .

Пришли к уравнению первого порядка с разделяющимися переменными относительно переменной x и новой искомой функции t(x). Заменяя и разделяя переменные, получим

; .

Проинтегрируем обе части полученного уравнения

Интеграл, стоящий в правой части является табличным .

Найдем интеграл от дробно рациональной функции, стоящей слева. Для этого можно, например, разложить подынтегральную функцию на сумму простейших или, выделив в знаменателе полный квадрат и сделав замену переменной, прийти к табличному интегралу.

Тогда, возвращаясь к исходному уравнению, получим

, ,

, .

Возвращаясь к старой переменной, получим

.

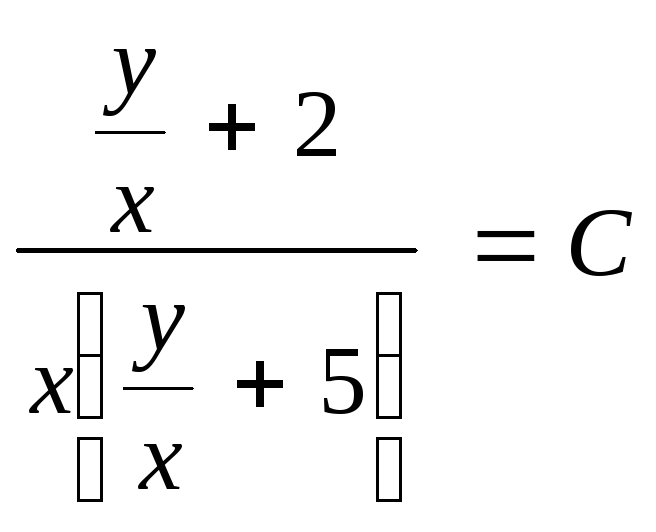Откуда после преобразований записываем общий интеграл

.

Проверка выполняется аналогично тому, как это делалось в предыдущих заданиях.

Ответ: общий интеграл .

Задание 2c. .

Данное уравнением является уравнением первого порядка. Рассмотрим функцию . Эта функция является однородной функцией нулевой степени, так как для произвольного действительно числаa выполняется равенство

Таким образом, данное уравнение является однородным и его можно решить аналогично тому, как это показано в пункте a), предварительно разделив числитель и знаменатель правой части на .

.

Сделаем замену переменной

или ,;

; .

Пришли к уравнению первого порядка с разделяющимися переменными относительно переменной x и новой искомой функции t(x).

; ;.

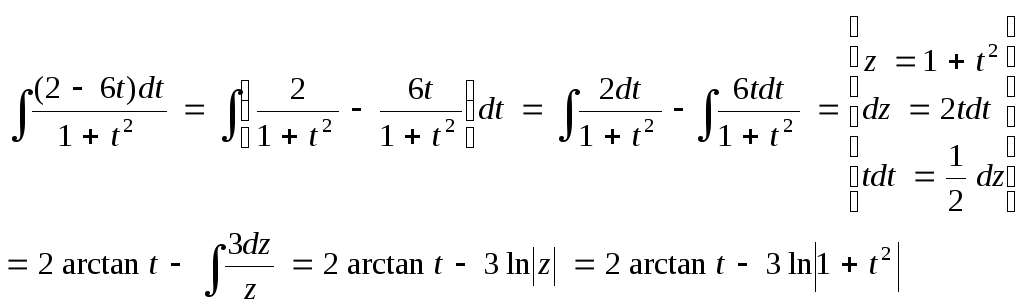
Тогда

,

,

,

,

,

.

Таким образом, общий интеграл исходного уравнения примет вид:

.

Проверку выполняется аналогично предыдущим примерам.

Ответ: общий интеграл .

Задание 2d. .

Рассмотрим функции ,. Эти функции являются однородными первой степени относительно переменныхx и y. Действительно:

,

.

Тогда исходное уравнение может быть сведено к уравнению вида (9), а затем к виду (11).

,

,

.

Заметим, что полученное уравнение совпадает с уравнением из задания 2(a), то есть пришли к случаю, который уже рассмотрен.