4.2. Множення чисел представлених у формі з фіксованою комою на двійковому суматорі прямого коду

 

Нехай задані машинні зображення двох чисел: [А]_пр =Sg_A, а₁а₂…a_n

[В]_пр = Sg_В, b₁b₂…b_n

Тоді їх добуток

C_пр = Sg_c, c₁c₂…c_n

де Sg_c – Sg₁ Sg_B; - знак додавання за модулем 2.

При виконанні цієї операції повинні бути задані структурова схема пристрою, на якому проводиться операція, і метод множення.

 

Приклад 4.1. Помножити числа [А]_пр=1.11010 і [В]_пр=0.11001

При множенні будуть використовуватися метод 2 і пристрій, зображений на рис.4.2

Запис усіх дій, що виконуюються пристроєм виконується за допомогою умовних позначень, тобто: = - оператор присвоювання означає, що блоку, що вказаний зліва від оператора, присвоюється значення, вказане справа від оператора; - зсув вмісту регістру [Рг А] на один розряд вправо; [СМ] – вміст суматора СМ; ПП – початкове положення.

Розвязок: Знак добутку визначаємо окремо від цифрової частини у відповідності з рівнянням:

Sg_c = Sg₁ Sg_B=10=1

Отримання цифрової частини можна показати в результаті наступного запису. Нехай суматор має 10 розрядів без врахування знаку, а регістри – 5 розрядів без знаку. Введем позначення відповідно цифрової частини множеного і цифрової частини множника.

Послідовність дій в процесі виконання операцій представлена у вигляді таблиці 4.1

Відповідь: [С]_пр=1.1010001010.

 

 

Рис 4.2. Структурна схема пристрою множення

 

Таблиця 4.1

Суматор	Регістр В	Примітка
0000000000 + 11010	11001       -1100 --110 ---11       ----1	ПП:[СМ]: = 0; [РгА]: = [А']; [РгВ]: = [В];   b5=1; [СМ] := [СМ] + [РгA]; []→; []→; b4 = 0; []→; []→; b3 = 0; []→; []→; b2=1; [СМ]:= [СМ] + [РгA] []→; []→;       b1= 1; [СМ]:= [СМ] + [РгА];     []→; []→; Кінець
1101000000 0110100000 0011010000 0001101000 + 11010
1110101000 0111010100 + 11010
10100010100* 1010001010

 

* Якщо в процесі виконання множення виникає одиниця переносу зі старшого розряду, то її треба зберігати.

Щоб процес множення відбувався правильно, необхідно передбачити блокування вироблення сигналу переповнення, так як можливе тимчасове переповнення на якомусь кроці множення (див. приклад 4.1). Приклад показує, що в даному випадку не обов'язково мати суматор довжиною 2n розрядів. Зберігання «хвостів» множення можна здійснювати в вивільнюваних розрядах регістра множника. Для цього достатньо забезпечити ланцюг передачі інформації з молодшого розряду суматора в старшин розряд регістра множника.

У всіх наведених нижче прикладах буде використано розглянутий спосіб.

 

4.3. Особливості множення чисел представлених у формі з плаваючою комою

Для чисел, представлених у формі з плаваючою комою, обов'язковим є представлення у вигляді мантиси і порядку (характеристики). При операції множення дії, які виконуються над мантисами і порядками, різні: мантиси перемножуються, порядки складаються. Очевидно, що результат множення може вийти ненормалізованном, тоді буде потрібно нормалізація з відповідною корекцією порядку результату. Отже, структурна схема розмножувального пристрою повинна змінитися (рис.4.3).

 

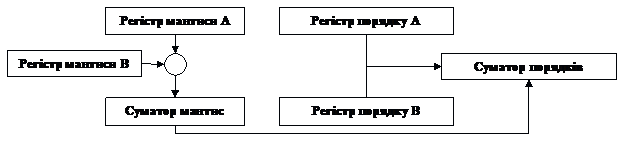
Рис. 4.3. Структурна схема пристрою множення з плаваючою комою

 

Розглянемо приклад виконання операцій множення чисел, заданих в прямому коді.

 

Приклад 4.2. Перемножити числа А = - 0,11001∙2^-3 і В = 0,10011∙2 ⁺¹.

Як пристрій множення використовується схема, показана на рис. 5.3, де РгА і РгВ - відповідно регістри для порядків р_А і р_В.

Розвязок: Мантиси перемножуються за правилами, розглянутим для чисел, представлених у формі з фіксованою комою. Для перемножування мантис використовується суматор прямого коду, а для складання порядків - суматор зворотного коду.

Спочатку записуються машинні зображення чисел:

[m_A]_пр=1.11001; [р_А]_об=1.100;

[m_B]_пр=0.10011; [р_В] _об= 0.001;

 

Послідовність дій у процесі виконання операції множення мантис представимо в табл.4.2.

Після виконання зазначених дій знаходиться мантиса добутку [m_C] _пр = 1,0111011011.

Одночасно з цим над порядками проводиться операція додавання:

[p_C] об = [p_A] об+ [p_B] об = 1,100 + 0,001 = 1,101.

Так як мантиса результату не задовольняє умові нормалізації (порушена ліва межа: = 1,= 0), товиконується зсув мантиси ліворуч на один розряд: [m_С] _np = 1,1110110110, і корекція порядку [р'_С]_об = [р_С]_об+ 1,110 = 1,101+1,110 = 1,110.

Таблиця 4.2

Знак результату	Суматор	Регістр В	Примітка
Sgc = Sg1 SgB=10=1	00000 + 11001	10011	РгmB: = [mB]; РгmA = [mA] РгpA = [рA]; PrpB: = [pB]; СМM: = 0; B5=1;.СМm:= [СМm] +[ РгmA]; []; [];   B4=1; СМm:= [СМm] + [РгmA];     []; []; b3 = 0; []; []; b2 = 0; []; [];     b1 = 1; СМm:=[СМm]+ [РгmA];   []; []; Кінець
	11001 011001 + 11001	01001
	1001011 1001011 01001011 001001011 + 11001
		00100 00010 00001
	111011011 0111011011
		00000

 

Якщо суматор мантис містить тільки n розрядів, то після округлення виходить вихідний результат.

Відповідь: З = - 0,11110∙2^-3.

 

При виконанні операції множення може мати місце ряд особливих випадків. Наприклад:

якщо один із співмножників дорівнює нулю, то добуток також дорівнює нулю. Отже, необхідно передбачити блокування виконання алгоритму множення і формувати результат, рівний нулю;

якщо порядок результату дорівнює найбільшій негативній величині, то необхідно формувати машинний нуль.

Ці особливі випадки можна передбачити в алгоритмі операції введенням аналізатора співмножників на нуль на початку операції (перший випадок), або корекцією добутку на підставі ознак результату (другий і третій випадки).