Тема 8. Форми представлення функцій алгебри логіки

 

8.1. Методи представлення булевих функцій

8.2. Аналітичне подання булевих функцій

 

8.1. Методи представлення булевих функцій

Найбільш часто на практиці використовуються табличне, кубічну та аналітичне подання булевих функцій. Розглянемо докладніше ці методи.

1. Табличне подання. Будь-яка булева функція, що залежить від L змінних, може бути представлена таблицею істинності, яка містить рядки іL+1 стовпцi. Рядки таблиці містять двійкові вхідні набори, які відповідають десятковим цифр від 0 до -1. В останній колонці таблиці задається значення функції на кожному наборі.

Приклад 8.1. Поставити у вигляді таблиці істинності функцію голосування щодо прийняття результату у важкій атлетиці. Змагання судять головний суддя і два бокових судді. Результат зараховується, якщо не менше двох суддів вважають вагу узятою, причому один з них - головний суддя.

Нехай y1 - функція голосування, при цьому y1= 1, якщо вага врахована. Позначимо результат голосування головного судді буквою а, а решту суддів змінними b і с. Якщо результат зарахований, то змінна відповідного судді встановлюється в одиницю. Функція y1 задана в табличній формі (Табл. 8.1).

Якщо число одиниць в наборі не більше однієї, то вага не зараховується (набори 0-2, 4); якщо число одиниць дорівнює двом, але головний суддя проти, то вага не зараховується (набір 3); якщо число одиниць в наборі не менше двох і головний суддя за, то вага зараховується (набори 5-7).

Приклад 8.2. Поставити таблицю істинності мажоритарної функції трьох змінних y2 =f(а, b, с).

Мажоритарна функція приймає значення, рівнозначно більшості елементів набору. Таблиця істинності функції y2 наведена в табл. 8.2.

Таблиця 8.1 Таблиця 8.2

a	b	c	y1		а	b	с	y2
0	0	0	0		0	0	0	0
0	0	1	0		0	0	1	0
0	1	0	0		0	1	0	0
0	1	1	0		0	1	1	1
1	0	0	0		1	0	0	0
1	0	1	1		1	0	1	1
1	1	0	1		1	1	0	1
1	1	1	1		1	1	1	1

 

 

 

 

 

 

 

 

Мажоритарні функції широко використовуються для прийняття рішень при резервуванні ресурсів. Наприклад, три комп'ютери управляють атомним реактором. В якості управлінського рішення вибирається те, яке виробляється більшістю. При цьому фіксується збій у роботі третього комп'ютера, і він підлягає ремонту. Без дефектна робота системи управління відповідає наборам 0 і 7.

Табличне представлення функцій є найбільш наочним і найбільш просто формується. Ця форма є первинною, а потім вона модифікується для введення інформації в ЕОМ або для оптимізації функцій і синтезу схеми. Однак табличне представлення є громіздким і не дозволяє компактно представити булеву функцію.

2. Кубічне подання. Кожному набору L, булевих змінних може бути поставлена у відповідність точка L- мірного простору в системі L координат. Так як змінні є булевими, то і простір називається L-мірним булевим простором або L-кубом.

На рис. 8.1 показано кубічне подання функцій L булевих змінних при L = 0,1,2,3. Домовимося, що якщо функція дорівнює одиниці на будь-якому наборі, то відповідна вершина куба обводиться знаком О.

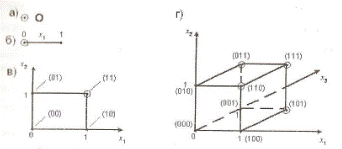
Рис. 8.1 Кубічне представлення булевих функцій

Рис. 8.1а відповідає випадку L= 0, при цьому функції є константами. Так, на рис. 8.1 (а) задана константа 0. Таким чином, булевим функціям при числі змінних L = 0 відповідають 0-куби.

Рис. 8.1 (б) задає функцію . Функції однієї змінної відповідають ребру або 1-куб.

Рис. 8.1 (в) задає функцію . Функції двох змінних відповідає грань або 2-куб. У дужках біля кожної вершини записано значення вхідного набору, який відповідає цій вершині. Набори записуються в порядку зростання індексу булевої змінної. Для функції двох змінних набори відповідають парам ().

Рис 8.1 (г) задає мажоритарну функцію (Табл. 8.2). Функції трьох змінних відповідає 3-куб, тобто куб, що має три виміри. З зростанням числа вимірів куби починають відрізнятися від звичних геометричних фігур. Як випливає з аналізу рис. 8.1 (г), 3-куб може бути представлений як два 2-куба для змінних . Однойменні вершини цих кубів з'єднані ребрами, протилежними кінцям яких відповідають протилежні значення змінної.

Аналогічним чином куб функції L змінних може бути представлений як два куби функції L - 1 змінних. Одному з цих кубів відповідає, наприклад, значення хL = 0, другому - хL = 1.

Кубічне уявлення є потужним засобом для введення інформації про булеві функціях в ЕОМ для подальшої обробки. Наприклад, вершини 3-куба 101 і 111 пов'язані ребром (Рис. 8.1 г). Інформація про це ребро представляється як 1 * 1, де * означає змінюваний елемент набору. Аналогічно, вершини 010, 01 1, 110, 111 входять в одну грань 3-куба (Рис. 8.1 г) і інформація про цю грань може бути представлена як *1*. Таким чином, якщо вершин єn- кубом, що входять в L- куб, то вони можуть бути представлені одним вектором, у якого n елементів замінені символом *. Це уявлення є більш компактним, ніж таблиця істинності.

Ще однією формою завдання булевих функцій є плоскі розгортки кубів, звані картами Карно. Карта Карно для функції L булевих змінних містить осередків, кожна з яких відповідає одному набору вхідних змінних. Карта Карно зберігає важливу властивість куба - набори для сусідніх клітин відрізняються тільки значенням однієї з змінних. Отже, будь-якісусідні клітини карти Карно відповідаютьn- кубу (n = 0,1 ,...,L).

На рис. 8.2 представлені карти Карно для функцій, які були представлені кубами на рис. 8.1.

Рис.8.2 Представлення булевих функцій картами Карно

Для побудови карти Карно для L- змінних скористаємося наступним методом:

1. Намалювати 2 карти Карно для (L-1)-й змінної.

2. Розмітити другу карту як дзеркальне відображення першою.

3. У першій карті для всіх клітин заповнити першу позицію нулями.

4. У другій карті для всіх клітин заповнити першу позицію одиницями.

5. Поєднати дві карти в одну.

Скористаємося цим правилом для побудови карти Карно для L = 3, проілюструвавши процес рисунком 8.3.

Після застосування першого та другого етапів маємо дві карти Карно для L = 2 із симетричною розміткою (Рис.8.3 а). Після виконання третього етапу маємо дві карти з різною розміткою (Рис.8.3 b), з'єднання яких дає карту Карно для L= 3. В осередках підсумкової карти записані набори відповідні цим осередкам (Рис.8.3 в).

Аналогічно будуються карти Карно для L = 4 (показано на Рис. 8.4 а) L= 5 (показано на Рис. 8.4 б), а також карти Карно для будь-якого параметра L.

Карти Карно є більш компактною формою подання булевих функцій, ніж таблиці істинності. Однак більш важливим їх застосуванням є використання карт для ручного мінімізації функцій, про що йдеться далі. Методи ручної мінімізації є основою для мінімізації з допомогою ЕОМ.

Для оптимізації функцій необхідно вміти знаходити сусідні клітини карти Карно, а також виділяти n- куби функції L змінних, де n = 0,1 ,...,L-1.

З рис. 8.1 б випливає, що при L = 2 кожна вершина 2-куба має дві сусідні вершини. З рис. 8.1 г слід, що кожна вершина 3-куба має 3 сусідні вершини. Аналогічно, кожна вершина L- куба має L сусідніх вершин. Таким чином, кожна клітина карти Карно для функції L змінних має L сусідніх клітин.

Рис. 8.3 Формування карт Карно для L=3

Знайдемо, наприклад, клітинки, сусідні клітки яких 00010 (Рис. 8.4 б). Три клітини знаходяться безпосередньо поруч - це 00011, 00110 і 01010. Щодо осі а клітинка 00010 є сусідньою з клітиною 00000, а щодо осі d - з клітиною 10010. Таким чином, всі п'ять сусідів знайдені.

Розглянемо клітини, відмічені знаком "-" (Рис. 8.4 б ). Це клітини 00000, 10000, 00100, 10100. Перша пара клітин відповідає ребру 0000, друга - ребру * 0100. Порівняння цих ребер показує, що вони відрізняються по третій координаті, тобто їм відповідає грань * 0*00. Аналогічно, клітках, зазначеним знаком "+" (Рис. 8.4 б), відповідає грань куба * 1 * 00. Порівняння цих граней показує, що клітинам, зазначеним знаками "-" і "", відповідає наступний 3-куб: *** 00. Знаходження різних n- кубів всередині L- куба (n = 0,1 ,..., L-1) вимагає деяких практичних навичок, одержуваних шляхом тренування. Відзначимо, що ці навички необхідні для подальшої мінімізації булевих функцій, заснованої на використанні Карг Карно. Очевидно, що пошук сусідніх клітин необхідний тільки в тому випадку, якщо мінімізація функції проводиться.

Рис. 8.4 Карти Карно для L=4(a) i L=5(b)

 

8.2. Аналітичне подання булевих функцій

Табличне і кубічне подання функцій є початковими формами, за якими формуються аналітичні вирази, які є основою для синтезу комбінаційної схеми. У рамках даної книги ми розглянемо дві канонічні форми подання булевих функцій.

1. Диз'юнктивна нормальна форма булевої функції.

Диз'юнктивна нормальна форма (ДНФ) формується як диз'юнкція елементарних кон'юнкція.

Розглянемо деяку функцію (Табл. 8.3) і визначимо її мінтерF1, відповідний набору x1= 0, х2 = 0, х3 = 1. З визначення мsнтерма випливає, що булева функція F1 дорівнює одиниці, якщо дорівнює одиниці кон'юнкція НЕ (x1) i НЕ (x2) i х3, таким чином маємо формулу Щоб перевірити наше припущення побудуємо таблицю для визначення значення булевої функціїF1 на всіх можливих восьми наборах вхідних змінних (Табл. 8.4). Ця таблиця має деяким розширення в порівнянні з класичною таблицею істинності

Таблиця 8.3

Х1	Х2	Х3	Y1
0	0	0	0
0	0	1	1
0	1	0	1
0	1	1	0
1	0	0	0
1	0	1	1
1	1	0	0
1	1	1	1

Таблиця 8.4

 

Х1	Х2	Х3
0	0	0	1	1	0	0
0	0	1	1	1	1	1
0	1	0	1	0	0	0
0	1	1	1	0	1	0
1	0	0	0	1	0	0
1	0	1	0	1	1	0
1	1	0	0	0	0	0
1	1	1	0	0	1	0

Друга частина табл. 8.4 містить додаткові стовпці , , Х3, що відповідає набору 001. Як видно з аналізу цієї таблиці, набору 001 відповідає комбінація , , Х3, рівна 111. Згідно з визначенням кон'юнкції, мінтерм F1 дорівнює одиниці саме для цього випадку.

У загальному вигляді мінтерм може бути представлений наступним чином:

(8.1)

Де - значенняl-го розряду h-го набору вихідних змінних,

Скориставшись формулою (8.1), визначимо мінтерми F2, F5, F7, відповідним розділами, де функція у1(Табл. 8.2) дорівнює одиниці. Це наступні мінтерми:

Отже, для формування мінтерма Fh необхідно записати кон'юнкцію х1, x2….. xL і поставити знак заперечення над змінними, які приймають нульове значення в h-му наборі.

Очевидно, що в кожний момент часу змінні xl (l =) мають якесь стабільне значення, відповідне конкретному набору. Таким чином, в кожен момент часу тільки один з усіх мінтермів функції може бути рівним одиниці. З огляду на цю властивість, побудуємо таблицю, задану залежність функції у1 від її мінтермів F1, F2, F5, F7 (табл.8.5).

Таблиця 8.5

				Набір
0	0	0	0	0, 3, 4, 6	0
1	0	0	0	1	1
0	1	0	0	2	1
0	0	1	0	5	1
0	0	0	1	7	1

Перший рядок таблиці відповідає ситуації F1 = F2 = F5 = F7 = 0. З аналізу табл.8.3 очевидно, що ця ситуація відповідає одному з наборів 0, 2, 4 або 6. Отже, функція у1 дорівнює нулю, якщо і тільки якщо виконується умова F1 = F2 = F5 = F7 = 0. Таким чином, функція у1 є диз'юнкцією мінтермом: .

З попереднього випливає, що ДНФ довільної булевої функції формується таким чином:

1. Виписуються мінтерми, відповідні розділами, на яких функція дорівнює одиниці.

2. Отримані мінтерми функції далі об'єднуються знаком диз'юнкції.

Наприклад, використання цього підходу для функції у2 (Табл. 8.6) приводить до наступної ДНФ:

Таблиця 8.6

Х1	Х2	Х3	Y2
0	0	0	0
0	0	1	0
0	1	0	1
0	1	1	1
1	0	0	0
1	0	1	0
1	1	0	1
1	1	1	0

Аналогічним способом, ДНФ може бути представлена по карті Карно. Наприклад, для функції у3 (Мал. 8.5) маємо:

Очевидно, що таблиці істинності, карти Карно та ДНФ є взаємозамінними формами подання булевих функцій. Ми розглянули, яким чином по карті Карно можна отримати ДНФ булевої функції. Тепер розглянемо зворотний процес.

Рис. 8.5 Карта Карно для функції

Нехай задана наступна ДНФ функції , побудуємо її таблицю істинності і карту Карно. З аналізу ДНФ функції у4 випливає, щоL = 3 і функція дорівнює одиниці на наборах 1, 3, 7. Таким чином, в рядках таблиці істинності та клітинах карти Карно для цієї функції, відповідних розділами 1, 3 і 7, повинні бути записані одиниці, а в інших - нулі (табл. 8.7 і рис. 8.6 відповідно).

Таблиця 8.7

Х1	Х2	Х3	Y4
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	1
1	0	0	0
1	0	1	0
1	1	0	0
1	1	1	1

 

Рангом кон'юнкції назвемо число вхідних в неї букв. Якщо всі терми ДНФ функції L змінних мають ранг L, то це досконала ДНФ (СДНФ). Таким чином, ми розглянули методи формування СДНФ за таблицями істинності і картам Карно.

Рис. 8.6 Карта Карно для функції

Термін "мінтерм" означає "мінімальний терм, що пов'язано з тим, що мінтерм відповідає 0-кубу, тобто кубу мінімального можливого розміру.

2. Кон'юнктивна нормальна форма булевої функції.

Кон'юнктивна нормальна форма (КНФ) булевої функції формується як кон'юнкція елементарних диз'юнкцій, званих екстремкмами.

Екстремум Фh називається булева функція, яка дорівнює нулю тільки на наборі з номером h, де h = 0, .. ., -1, деL - число вхідних змінних.

Розглянемо екстремум Ф3 функції у1 (Табл. 8.3). Побудуємо таблицю істинності булевої функції Ф3 (Табл. 8.8).

 

Таблиця 8.8

Х1	Х2	Х3	Х1
0	0	0	1	1	1	1
0	0	1	1	1	0	1
0	1	0	1	0	1	1
0	1	1	1	0	0	0
1	0	0	0	1	1	1
1	0	1	0	1	0	1
1	1	0	0	0	1	1
1	1	1	0	0	0	1

На даній таблиці показано, що функція являється дизюнктивоню формою застосованих Х1 , Х2 і :

Відповідно, для формування необхідно записати дизюнкцію вхідних змінних, причому, якщорівняється або рівне 1(0) наh наборі, то в входить її інверсне (пряме) значення. Маємо наступну форму:

(8.2)

У формулі (9.2) всі компоненти мають той же зміст, що й у формулі (8.1).

Очевидно, що в кожний момент часу може бути рівний одиниці тільки один екстремум. Побудуємо таблицю, задану залежність функції у1 від її екстремуму Ф0, Ф3, Ф4, Ф6, де функція дорівнює нулю (Табл. 8.9).

Як випливає з аналізу цієї таблиці, функція у1 дорівнює одиниці, якщо тільки всі її екстремуми рівні одиниці, тобто маємо формулу:

Таблиця 8.9

1	1	1	1	1
0	1	1	1	0
1	0	1	1	0
1	1	0	1	0
1	1	1	0	0

Таким чином, для побудови КНФ довільної булевої функції застосовна наступна процедура:

1. Виписати екстремуми, які відповідають вхідним набором, на яких функція дорівнює нулю.

2. Отримані екстремуми об'єднуються знаком кон'юнкції. Наприклад, для функції у2 (Табл. 9.6) маємо формулу:

Аналогічним чином КНФ може бути побудована по карті Карно. Наприклад, для функції y3 (Рис. 2.5) маємо:

Пояснимо походження терміну "екстремум". Розглянемо екстремум і визначимо вершини 3-куба, які йому відповідають.

Змінна х1 у формулі Ф1 відповідає межі 1 **, а змінна х2 - * 1 * і, нарешті, змінна - ** 0. Грань 1 ** включає вхідні набори 100, 101, 11О, 111 грань * 1 *- 010,011, 110, 111, грань. ** 0 - 000, 010, 100, 110. Таким чином, екстремум Ф1 відповідає всім наборам при числі змінних L = 3 (крім набору 001). Отже, екстремум покриває -1 набір, тобто максимально можливу кількість наборів, які не є в сукупності Т-кубом.

За аналогією з СДНФ, КНФ називається досконалою, якщо всі її екстремуми мають ранг L, де L - число змінних, від яких залежить вихідна булева функція.

Всі розглянуті форми представлення булевих функцій є взаємно-однозначними, тобто але кожний з цих форм можуть бути отримані всі інші. Зауважимо, що для переходу СДНФ до СКНФ і навпаки необхідно перейти до однієї з інших форм представлення. Цей факт відображено на рис. 8.7, де двонаправлені ребра відображають факт еквівалентності (тобто, одна форма подання може бути замінена іншою) різних форм представлення однієї і тієї ж функції.

Мал. 8.7 Взаємозв’язок між формами представлення булевої функції

При синтезі схем вузлів ЕОМ доцільно використовувати обмежений набір логічних елементів. Чим менше елементів у наборі, тим простіше налагодити виробництво надійних схем. До цього набору видається наступну вимогу - будь-яка скільки завгодно складна логічна схема може бути побудована з елементів цього набору. Технічне завдання відшукання такого набору логічних елементів зводиться до математичної задачі визначення функціонально повного набору булевих функцій.

Система булевих функцій називається функціонально повною, якщо будь-яка булева функція може бути виражена у вигляді суперпозиції цих функцій. З матеріалу попередніх розділів ясно, що система функцій {І, АБО, НЕ} буде функціонально повною, так як вона дозволяє висловити ДНФ і КНФ довільної булевої функції.

Очевидно, що якщо будь-яку функцію довільній функціональної системи можна Ψ1 виразити через функції деякої системи Ψ2, то система Ψ2 так само є функціонально повною.

Знайдемо деякі функціонально повні системи булевих функцій, що мають практичне значення. Уявімо базис {І, АБО, НЕ} у вигляді . Тоді справедливо наступне:

1. Система функціонально повна, так як. Це означає, що система {НЕ, АБО} дозволяє висловити всі функції, які входять у функціонально повну систему {І, АБО, НЕ}.

2. Система функціонально повна, тому що. Це означає, що система {НЕ, І} дозволяє висловити всі функції, які входять у функціонально повну систему {І, АБО, НЕ}.

3. Система Функціонально повна. Для доказу розглянемо наступні рівняння:,. Отже, функція Шиффера визначає функціонально повну систему.

4. Система функціонально повна, тому щоі. Це означає, що функція Пірса дозволяє отримати будь-яку функцію з функціонально повної системи.

5. Система функцій є функціонально повною, так якТобто ця система дозволяє висловити будь-яку функцію базису. З повнотою цього базису пов'язана алгебра Жегалкіна. У цій алгебрі будь-яка булева функція представляється поліномом Жегалкіна, тобто сумою за модулем два кінцевого числа кон'юнкцій змінних без знаків інверсій.

У нашій книзі, як правило, використовується базис І-НЕ або АБО-НЕ, тобто базис, заснований на функціях Шеффера і Пірса. Відмітимо, що перший з цих базисів отримав найбільше використання при проектуванні практичних вузлів ЕОМ.