Тема 3. Арифметичні операції в двійковій сч. Додавання і віднімання чисел.

Основною операцією, яку використовують у цифрових систе­мах під час виконання різних обчислень, є операція алгебраїчного додавання. її виконують на основі правил виконання операцій у двійковій системі зображення чисел, які для однорозрядних чисел мають такий вигляд:

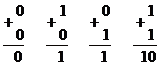
Перенесення до старшого розряду здійснюють тоді, коли в од­ному розряді обох складових є одиниці. Операцію знаходження суми у багаторозрядних числах виконують послідовно, почина­ючи з молодшого розряду. У зв'язку з цим, починаючи з другого розряду, виконують складання трьох цифр - двох розрядних скла­дових і перенесення з молодшого розряду.

Приклад 3.1. Скласти два додатні двійкові числа .

Розв'язання. Під час виконання операції додавання мають місце перепов­нення у першому та четвертому розрядах і, відповідно, перенесення одиниці з першого розряду у другий і з четвертого у п'ятий.

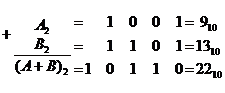
Операцію віднімання у цифрових схемах виконують за допо­могою операції додавання, зображуючи від'ємник у доповняль­ному коді.

Приклад 3.2. Знайти суму двох чисел і з викори­станням доповняльного коду.

Розв'язання. Для виконання вказаної операції у десятковій системі чис­лення необхідно для числа K знайти відповідний доповняльний код. Його знаходять за тими ж правилами, що й у двійковій системі. Обернений код числа знаходять як доповнення до дев'ятки цифри кожного розряду. Для чис­ла обернений код

Доповняльний код для числа К:

Виконаємо операцію додавання. При цьому введемо знакові розряди, які позначимо апострофом, що встановлюєтьсяпісля знакової цифри:

Перенесення, що з'являється зі знакового розряду, відкидаємо.

Аналогічно виконують операцію віднімання у двійковій систе­мі числення.

Приклад 3.3. Додати два числа і

Розв'язання. Знаходимо доповняльний код від'ємного числа K:

Знаходимо суму:

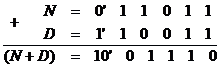
Відкидаючи 1 переносу у знаковому розряді, отримуємо:

Приклад 3.4. Змінимо знаки обох чисел на зворотні:

Розв'язання. Доповняльний код від'ємного числа

Знаходимо суму:

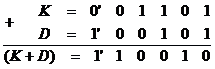
Знаковий розряд засвідчує, що результат операції від'ємний, а число зоб­ражене у доповняльному коді. Для отримання результату у прямому коді необхідно спочатку перейти до оберненого коду, віднімаючи одиницю від результату виконання арифметичної операції, а потім - інвертувати.

Знаходимо обернений код результату:прямий код:

Пряму операцію віднімання з використанням операцій пози­чення зі старших розрядів застосовують лише для порівняння двох кодів, адже відсутність чи наявність позичення зі старшого розря­ду дає можливість легко визначити більше з порівнюваних чисел.

Розглянемо тепер особливість виконання операцій у двійково-десятковій системі числення (код 8-4-2-1). Виконують операції на основі правил двійкової арифметики. Якщо одержане число пере­вищує , то повинна формуватися одиниця перенесення, яка передається до наступного десяткового розряду. Але результат відрізнятиметься від правильного, і в нього необхідно внести відпо­відний коректив. Наявність у результаті операції числа, що пере­вершує дев'ятку, легко виявляють за рядом ознак, які читач може сформулювати самостійно.

Приклад 3.5. Скласти числа і використанням коду 8-4-2-1.

Розв'язання. Оскільки результат менший десяти, то корекція не потрібна.

Приклад 3.6. Скласти числаі

Розв'язання. У цьому випадку результат більший десяти, тому необхідно вносити ко­рекцію.

Поява одиниці у п'ятому розряді означає, що число, представлене чотир­ма молодшими розрядами, збільшилось на 16 одиниць. Але, з іншого боку, одиниця передалась у старший десятковий розряд, що еквівалентно числу 10, тому в молодшому розряді не вистачає шістьох одиниць. Це означає, що необхідно до результату додати корекцію - шість одиниць, тобто:

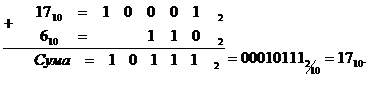
Результат представлено одиницею в розряді десятків і сімкою в розряді одиниць.

Приклад 3.7. Скласти числа

Розв’язання :

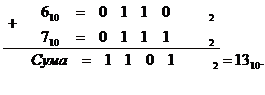
У цьому прикладі перенесення у п'ятий розряд немає, але результат перевер­шує дев'ятку, тому необхідно внести корекцію. Корекція необхідна не тільки для того, щоб скоригувати результат молодших розрядів, а й для того, щоб перенести одиницю у старший десятковий розряд. Знову додасться 10 і відніметься 16, тому для корекції необхідно додати цифру 6:

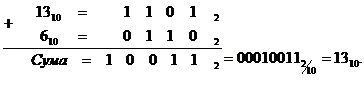
З двох останніх прикладів бачимо, що у першому випадку під час виконання операції має місце перенесення у старшу тетраду, що і може виступати ознакою необхідності корекції результату. У другому випадку такого перенесення немає, тому необхідно або передбачати можливість такого результату, або створювати допоміжні заходи для введення корекції. Як вихід з такої ситуації можна запропонувати використання самокоригувальних кодів -наприклад коду "з надлишком З".

Приклад 3.8. Виконати операцію знаходження суми двох чисел з попе­реднього прикладу у випадку використання коду "з надлишком З".

Розв'язання. Відповідні коди чисел: Після вико­нання операції додавання маємо результат:

У разі використання інших кодів для зображення десяткових Цифр правила знаходження суми зміняться, але логічний аналіз процедури легко дозволяє знайти правила корекції.

У випадку знаходження суми багаторозрядних двійково-десят­кових чисел від'ємні числа зображують в оберненому або допов­няльному коді. При цьому обернений код одержують за рахунок доповнення до 9. Якщо використовувати не код 8-4-2-1, а коди "з надлишком 3" або 2-4-2-1, то процедура формування доповнення до 9 значно спрощується.