RGR_2_Ekonom

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Черкасский государственный технологический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

однорідне диференціальне

підстановку: t

y tx dy tdx xdt y

.pdf

Скачиваний:

Добавлен:

23.02.2016

Размер:

962.14 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 54 5 > Следующая >>>

Контрольні запитання

1.Первісна. Загальний вигляд первісної.

2.Таблиця інтегралів від основних елементарних функцій.

3.Основні властивості невизначеного інтеграла.

4.Основні методи інтегрування.

5.Інтегрування дробово-раціональних функцій.

6.Означення визначеного інтеграла.

7.Основні властивості визначеного інтеграла.

8.Формула Ньютона-Лейбніца.

9.Методи обчислення визначених інтегралів.

10.Невласні інтеграли.

11.Застосування визначених інтегралів.

§3. Диференціальні рівняння

Основні поняття і теореми: [1. – ст. 614-657; 2. – ст. 352-368; 3. – ст. 315-

345; 4. – ст. 421-473].

Зразки розв’язування задач

Диференціальні рівняння І порядку

Задача 3.1

Знайти загальний розв’язок диференціального рівняння.

а)

(2x 2xy	2	)dx ( y

yx	2	)dy

Розв’язання

Це рівняння з відокремлюваними змінними:


								2x(1 y			2		)dx		y(1		x	2	)dy.
								2x(1 y					)dx		y(1		x		)dy.
Поділимо обидві частини частини на вираз																				(1 y		2	)(1		x	2	) :
Поділимо обидві частини частини на вираз																				(1 y			)(1		x		) :
2x(1 y			2		)dx			y(1 x				2		)dy			2xdx				ydy					4xdx			2 ydy
2x(1 y					)dx			y(1 x						)dy			2xdx				ydy					4xdx			2 ydy		.
(1 y	2			x		2		(1 y	2					x	2		1 x			2	1 y			2		1 x		2	1 y	2	.
	2	)(1				2	)		2	)(1					2	)				2				2				2		2
		)(1					)			)(1						)

Змінні відокремлено.

Інтегруємо обидві частині:


4xdx		2 ydy	2 ln(1 x2 ) ln(1						y2 ) ln C ln(1 y2 ) ln C(1 x2 )2

1 x2		1 y2
1 y	2	C(1 x		2	)	2	y	C(1	x	2	)	2	1 .
1 y		C(1 x			)		y	C(1	x		)		1 .

Відповідь: y 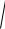C(1 x2)2 1 – загальний розв’язок диференціального

рівняння.

б) y y 2 8 y 12. x2 x

Розв’язання

Підставляємо цей вираз в початкове рівняння:

t x

8t 12

7t 12

Змінні відокремлено.

Інтегруємо обидві частини:

7t 12

Знайдемо обидва інтеграла окремо.

рівняння.

dy	t x	dt
dx		dx

xt 2

Використаємо

	dt	.
	7t 12	.
	7t 12

	dx		ln x ln C1 ln C1 x .
		x

			dt				dt
		2				(t 3)(t 4)
	t		7t	12

ln C				x ln C			t 3	Cx
					2
			1				t 4



t t

	3	, де
	4	, де
	4

1
	dt
t
t	4

		C
	C	1
	C	C
		C
		2

ln t 3 ln t 4 ln C	2
	2

Повертаємося до змінної y ,

або в явному вигляді:

y 3x

підставляючи t

y 3x

xy 4x2

y 4x

4Cx

C(xy 4x

) y

Відповідь:	y 3x	C , або

	xy 4x2

диференціального рівняння.


	4Cx		2	3x
y	4Cx			3x
y	1	Cx
	1	Cx

– загальний розв’язок

в)

Розв’язання

y	y	sin x	.
	x	x

Це лінійне диференціальне рівняння 1-го порядку.

Розв’яжемо це рівняння методом Бернуллі, який полягає в тому, що розв’язок рівняння будемо шукати у вигляді добутку двох функцій y u(x)v(x) , причому одна з цих функцій довільна (але не рівна нулю). Якщо

y uv


Оскільки u v
Відповідь:	y

sin x

u v uv

sin x

u v

sin x

u v

ln v ln x v

sin x

sin x u cos x C.

Отже

(C cos x).

C cos x

– загальний розв’язок даного рівняння.

Лінійні диференціальні рівняння ІІ порядку

Задача 3.2

Знайти розв’язок задачі Коші:

y			y 2e	2x	; y(0) 2;		1,	(1)
		2y				y (0)

Розв’язання

Це лінійне диференціальне рівняння 2-го порядку з постійними коефіцієнтами.

1) Спочатку знаходимо частинний розв’язок відповідного однорідного рівняння:

y 2y y 0,

(2)

Складаємо характеристичне рівняння: k	2	2k 1 0 (k 1)	2	0 .

Його корені:

k1,2 1

, тобто характеристичне рівняння має два однакових

кореня.

Тоді загальний розв’язок рівняння (2) буде:

y C1e

C2 xe

y C1e

C2 xe

2) Розв’язок рівняння (1) з правою частиною дорівнює сумі:

y y y *, де

y * – деякий частинний

розв’язок

рівняння

(1). Для

його

знаходження

використаємо правило:

, де Pn (x) –

Нехай права частина рівняння (1) має вигляд: f (x) Pn (x)e

многочлен степеня n .

Тоді якщо число

не

є коренем характеристичного

рівняння, то

y* Q(x)e

Якщо

однократним

коренем

характеристичного

y* xQ(x)e

Якщо

двократним

коренем

характеристичного

y* x

Q(x)e

де

Q(x) – многочлен степеня

n .

Тут

f (x) 2e

Pn (x) 2

– многочлен

(константа).

Число 2

не є коренем характеристичного рівняння

рівняння, то

рівняння то

0-го степеня

x	2x
y* Q(x)e	Ae

Знаходимо похідні

( y*) , ( y*)

іпідставляємо в ліву частину рівняння (1): y* Ae 2x

( y*) Ae

2Ae

( y*) 2Ae

4Ae

y 2 y y 2e

4Ae

2Ae

A 2.

Отже y* 2e

Тоді загальний розв’язок рівняння (1) буде:

y y y* y C1e

C2xe

3) Знаходимо розв’язок

задачі

Коші,

тобто

частинний

задовольняє початковим умовам

при x 0

y(0) 2, y (0)

розв’язок, що

: y 2,	y		1.

Підставляємо ці значення у загальний розв’язок диференціального

рівняння (1) і в його похідну:

y C e

C xe

y C e x C xe x 2e2x

C e x

e x xe x 4e2x

y(0) C e

0 2e

2 2

0 4e

y (0) C e

C C

4 1

Одержуємо систему двох рівнянь для визначення

і C2 :

C 2 2,

C 4,

C1 4; C2 1

C1 C2 4 1.

C1 C2 3.

y C e x

C xe x

2e 2x 4e x xe x 2e 2x

Відповідь:

y 4e

– розв’язок задачі Коші.

Найпростіші застосування диференціальних рівнянь в економіці

	Нехай Y t доход, який одержано на момент часу t		деякою галуззю,
виражається формулою:
	Y t I t C t ,		(3)
де	І t сума інвестицій;
	C t величина споживання.
	Будемо вважати, що швидкість збільшення	доходу пропорційна

величині інвестицій, тобто

b Y t I t ,

(4)

де b коефіцієнт капіталоємності приросту доходу.

Нехай

C t є фіксованою частиною одержуваного доходу на момент часу

, тобто C t 1 m Y t , де m норма інвестицій, 0 m 1			(стала величина).
Тоді 3 (3), (4) випливає :
	m	Y t .
Y t	b	Y t .
	b

Задача 3.3

Знайти функцію доходу визначається функцією C

Y (t) , якщо відомо, що величина споживання

2t , коефіцієнт капіталоємності приросту доходу

b	1	, Y 0 2.
	2

Розв’язання

Із співвідношень (3), (4) одержуємо, що

Y t 12 Y t 2t Y t 2Y t 4t, Y 0 2.

Отже, маємо лінійне диференціальне рівняння І порядку. Розв’яжемо його методом Бернуллі: Y t u t v t

Y uv Y u v uv і Y 2Y 4t

u v uv 2uv 4t

2v 0,

u v u v

2v 4t

u v 4t.

2dt ln v

2t v e

v 2v 0

4te

du 4te

Так як u v

te2t dt

e2t

e2t dt

u 4

4 t

dt, v

2te

Отже, Y t e

c Y t Ce

2t 1, C R.

Скориставшись початковою умовою

Y 0 2,

отримаємо

2 C 1 C 1.

Таким чином, функція доходу має вигляд

Y t e

2t 1.

РОЗРАХУНКОВІ ЗАВДАННЯ

Задача 10. Знайти загальний розв’язок диференціального рівняння.

а)

xydx 2 x2 dy 0;

11. а)

1 y2 dx y

1 x2 dy

б)

xy y

;

б)

2xy

;

в)

y yctgx e

cos x

;

в)

sin x

;

dx x

dy 0;

а)

y x

12.

а)

1 dy 2xdx 0;

б)

y e

;

б)

2 ln x;

в)

y 2 yctgx sin

в)

;

3.а)

б)

в)

4.а)

б)

в)

5.а)

б)

в)

6x 3xy

dx x

y y dy 0;

2xy

2 y

2 ;

y cos x

2 sin 2x;

2x 2xy

dx y yx

12;

1 e x 1 ;

dy xy2 x dx 0;

1 x2

10;

x3 ;

13. а) xdy y	2	y dx 0;

б) y xy 2 ln x;

в)

ytgx

;

cos x

14.

а)

1 2x dx y

dy 0;

б)

;

2 y

в)

x 1

;

x 1

15. а) 5e

tgydx

1 e

ydy

sec

б)

;

2 y

в)

;

6.а)

б)

в)

7.а)

б)

в)

8.а)

б)

в)

9.а)

б)

в)

xy2 x dx x2 y y dy 0;

xy y

1 ln

;

x 1

1dx y

1dy 0;

2 x 2x;

3 y

dx y x

dy 0;

x y

;

x y

2 1 y 2x;

3 x

y dy

2 y

dx 0;

xy 4

y ctgxy

cos x

;

sin

16.

а)

1dx xydy 0;

б)

x 4;

2 y

ex x 2

в)

;

17.

а)

2 dx 2x

ydy 0;

б)

;

в)

;

18. а) x

dx 4 x

y dy 0;

б)

x e

;

в)

y x

4x 5;

x 2

19. а)

2x 1 e

dy 0;

б)

x tg x ;

в)

10.а)

б)

в)

x 1 y

1 x

dy 0;

;

2 1 x

20. а) tgxsec2 ydx ctgy cos2 xdy 0;

б)	y	sin		y		y	;
				x		x


			y		x
		x xe .
в)	y	x xe .

<<< < Предыдущая 1 2 34 / 54 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
20.08.201952.16 Кб1PSPE.docx
#
25.09.201986.19 Кб1PSPE_full.docx
#
11.09.2019142.34 Кб2Rekomendatsiyi_shodo_vikonannya_organizatsiyno_...doc
#
21.07.2019276.61 Кб3RG .docx
#
23.02.201649.4 Кб8RGR_2.docx
#
23.02.2016962.14 Кб2RGR_2_Ekonom.pdf
#
23.02.2016134.66 Кб11RGR_Kosenko.doc
#
08.12.20181.63 Mб2RGR_poshta_bilan (Автосохраненный).doc
#
18.11.2019384 Кб26Rozdatkovy_material_1-6.doc
#
23.02.20161.9 Mб49rsu379.pdf
#
23.02.201615.96 Кб66seminar_4.docx