Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Черкасский государственный технологический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Laboratorni_roboti_ChM

.pdf

Скачиваний:

Добавлен:

23.02.2016

Размер:

2.05 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 66

Чисельні методи © Мірошкіна І.В.

Звіт про виконання лабораторної роботи повинен містити:

-формулювання задачі;

-листинг програми мовою Pascal;

-отримані чисельні результати;

-аналіз результатів;

-висновки.

КОНТРОЛЬНІ ПИТАННЯ

31.Коли застосовується чисельне інтегрування?

32.Що називається механічною квадратурою?

33.У чому міститься прийом механічної квадратури?

34.Який загальний геометричний зміст чисельних методів обчислення визначених однократних інтегралів?

35.Зміст методів прямокутників, їхня похибка.

36.Зміст методу трапецій, його похибка.

37.Зміст методу Сімпсона, його похибка.

38.Як обчислити інтеграл із заданою точністю?

			1	1
ПРИКЛАД ВИКОНАННЯ:Обчислимо інтеграл				1	dx при n=10:

				x 1
			0
	1	1
f (x)	1	I	f (x) dx
f (x)	1 x	0	I 0.69315

Для обчислення інтеграла чисельними методами задамо ситку значень по x:

	n 10	h 0.1	x0 0
	i 1 n	xi x0 i h
T	( 0 0.1 0.2 0.3	0.4 0.5 0.6	0.7 0.8 0.9 1)
x

і знайдемо значення підінтегральної функції в отриманих точках:
i 0 n	y	i	f x
			i

Для формули середніх прямокутників необхідно знайту значення функції в середніх точках:

ycp

yT ( 1 0.9091 0.8333 0.7692 0.7143 0.6667 0.625 0.5882 0.5556 0.5263 0.5)

ycpT ( 0.9524 0.8696 0.8 0.7407 0.6897 0.6452 0.6061 0.5714 0.5405 0.5128 0.4878)

Тоді за формулою лівих прямокутників:

n 1

Ileft h yk

k 0

Ileft 0.71877 Похибка:

left

I Ileft

left

0.02562

Тоді за формулою правих прямокутників:

Irigth h

k 1

Irigth 0.66877

rigth

I Irigth

rigth 0.02438

За формулою середніх прямокутників:

Чисельні методи © Мірошкіна І.В.

n 1

Imidle h

ycpk

10 4

k 0

Imidle 0.69284

midle

I Imidle

midle

3.1182

За формулою трапецій:

n 1

Itrap h

trap 6.24223 10 4

k 1

Itrap

0.69377

trap

I Itrap

За формулою парабол:

Iparab

Iparab 0.69315

parab

I Iparab

parab 3.05013

10 6

ЛАБОРАТОРНА РОБОТА № 8

ТЕМА: Чисельне розв’язування задачі Коші.

МЕТА: Опанувати чисельними методами розв’язання задачі Коші для звичайного диференційного рівняння першого порядку.

ТЕОРЕТИЧНІ ВІДОМОСТІ Задача Коші для звичайного диференційного рівняння першого порядку

формулюється так: знайти функцію

y y( x ),	(1)
що є розв’язком диференційного рівняння
y f ( x, y )	(2)
і задовольняє початковій умові
y0 y( x0 ).	(3)
Чисельні методи розв’язування задачі Коші подають розв’язок у вигляді
таблиці чисел, тобто знаходять значення функції (1) в окремих	точках xi
(i=0,1,2,…).

Найпростішим методом розв’язування задачі Коші (1)-(3) є метод Ейлера. Його ідея полягає в заміні інтегральної кривої (1), що проходить через точку M0 ( x0 , y0 ) ламаною лінією M0 M1M 2 ... з вершинами Mi ( xi , yi ) (рис. 1), які визначаються за ітераційними формулами:

								Чисельні методи © Мірошкіна І.В.
		xi x0		ih ,					(4)
		yi 1	yi		hf ( x, y ),		(i=0,1,2,…).		(4)
		yi 1	yi		hf ( x, y ),		(i=0,1,2,…).
	y								y=y(x)
									y=y(x)
					M2	M3		Mi+1
			M1			M3	Mi	Mi+1
			M1				Mi
	A0	M0
	A1	y0		y1	y2	y3	yi	yi+1
	Ai		h		h
			h		h				x
P	0 A2	x0		x1	x2	x3			x
P	0 A2	x0		x1	x2	x3
						Рис. 1.

Недоліком метода Ейлера є його низька точність, яка пропорційна величині h. Тобто, щоб уточнити результат на один десятковий знак, необхідно зменшити крок в десять разів. Тому цей метод застосовують для орієнтовних розрахунків.

Більш точним є вдосконалений метод “предиктор-коректор” (інша назва - метод Ейлера-Коші), за яким спочатку визначають “грубе” наближення розв’язку

~	yi	hf ( xi , yi ) ,			(5)
yi 1
звідки знаходять направлення інтегральної кривої:
~		~			(6)
fi 1	f ( xi 1 , yi 1 ) .
Потім вважають:		~

y	y	h	fi fi 1	, (i=0,1,2,…).	(7)

i 1	i	2

Похибка методу “предиктор-коректор” має порядок h2 .

В обчислювальній практиці найбільш часто використовують метод Рунге-

Кутти, який має точність пропорційну h4 . Приведемо його розрахункові формули:

xi 1 xi h,

yi 1 yi k1 2k2 2k3 k4 , 6

k1 hf ( xi , yi ),

hf ( x

, y

hf ( x

, y

hf ( xi h, yi

k3 ),

(i=0,1,2,…,n).

(8)

ЗАВДАННЯ

Чисельні методи © Мірошкіна І.В.

7.Знайти наближений розв’язок задачі Коші для звичайного диференційного рівняння першого порядку на заданому проміжку методами Ейлера, “предиктор – коректор”, Рунге-Кутти.

	y f ( x, y )									x0	y( x0 ) y0	b
1.	y			xy						0.0	1.0	1.0

		x2 y2
		x2 y2
2.	y x y 2									0.0	0.0	0.3
3.	y x2					y 2				0.0	0.27	1.0
4.	y x2		xy y2							0.0	0.1	1.0
5.	y x2		xy y2							0.0	0.0	1.0
6.	y xy e y									0.0	0.0	0.1
7.	y x sin							y
	y x sin									0.0	1.0	2.0
										0.0	1.0	2.0
							3
8.	y 2x cos y									0.0	0.0	0.1

9.	y xy3 y									0.0	1.0	1.0
10.	y				1					1.0	0.0	2.0

			y2 x
			y2 x
11.	y			1		xy				0.0	1.0	1.0
	y					xy				0.0	1.0	1.0
			2
12.	y xy2 1									0.0	0.0	1.0
13.	y ( 2 y )x									1.0	1.0	2.0

14.	y ln( x y )									0.0	1.5	1.0

15.	y cos x y									-1.0	0.0	0.0

16.	y 2 y 3ex									0.3	1.42	0.6
17.	y y 2					x2				1.0	1.0	2.0
18.	y xy( y 2 1 )									0.0	0.5	1.0
19.	y		2 y x							1.0	2.0	2.0
	y					y				1.0	2.0	2.0
						y

20.	y x3					y				1.0	-1.0	2.0
21.	y 2xy x2									0.0	0.0	0.5
22.	y ex				y2					0.0	0.0	0.4
23.	y x3					y 2				0.0	0.0	0.5
24.	y y2ex 2 y									0.0	1.0	1.0
25.						y

	y		x							1.0	1.0	4.0
	y		x							1.0	1.0	4.0
									54

								Чисельні методи © Мірошкіна І.В.
26.		y x2 y 2					0.0	0.0	1.0
27.				y		2
	y		x 1 y				0.0	1.0	1.0
	y		x 1 y				0.0	1.0	1.0
28.	y
28.	y				2x y		2.0	0.75	3.0

29.			y x e y				1.0	1.0	2.0
30.		y 2 x y 2					0.0	1.0	3.0

Звіт про виконання лабораторної роботи повинен містити:

-формулювання задачі;

-лістинг програми мовою Pascal;

-отримані чисельні результати;

-аналіз результатів;

-висновки.

КОНТРОЛЬНІ ПИТАННЯ

1.Сформулюйте задачу Коші для звичайного диференційного рівняння першого порядку.

2.Геометрична інтерпретація задачі Коші.

3.Сутність методу Ейлера, його точність.

4.Сутність модифікації метода Ейлера у методі “предиктор-коректор”.

5.Геометрична сутність метода Рунге-Кутти.

6.Які ще методи розв’язання задачі Коші Вам відомі?

ЗРАЗОК ВИКОНАННЯ ЛАБОРАТОРНОЇ РОБОТИ

1.Знайти наближений розв’язок задачі Коші для звичайного диференційного рівняння першого порядку на заданому проміжку методами Ейлера, “предиктор – коректор”, Рунге-Кутти:

	y 2 x	y 2	y(x0)=y(0)=1	на інтервалі [0; 0,5].
Задамо сітку по x:
x0 0
i 0 9	h 0.05

xi 1 xi h

x( 0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45 0.5)

Метод Ейлера:

f (x y) 2x y2

yE0 1
yE	yE h f x yE
i 1	i	i i

yET ( 1 1.1 1.212 1.339 1.484 1.652 1.848 2.08 2.361 2.705 3.139)

Метод «предиктор-коректор»:

yPK0 1 i 0 9

yPK

f x yPK f x

yPK

i 1

yPKT ( 1

1.106 1.227 1.365 1.525 1.714 1.94

h f xi yPKi

2.216 2.563 3.013 3.622)

yRi 1

yRT ( 1

								Метод Рунге-Кутти:
									yR0 1
z yRi
k1 h f x yR
			i	i
k2 h f		x		h	yR			k1
k2 h f		x			yR
		i		2		i		2
k3 h f		x		h	yR			k2
k3 h f		x			yR
		i		2		i		2
k4 h f xi h yRi k3
z z	1		(k1		2 k2		2 k3 k4)
z z			(k1		2 k2		2 k3 k4)
6

1.106 1.227 1.365 1.526 1.716 1.943 2.222 2.572 3.03 3.653)

Розв’яжемо тепер рівняння за допомогою функції Mathcad Odesolve:

Given

d y(z) 2z y(z)2 dz

y(0) 1

y Odesolve (z 0.5)

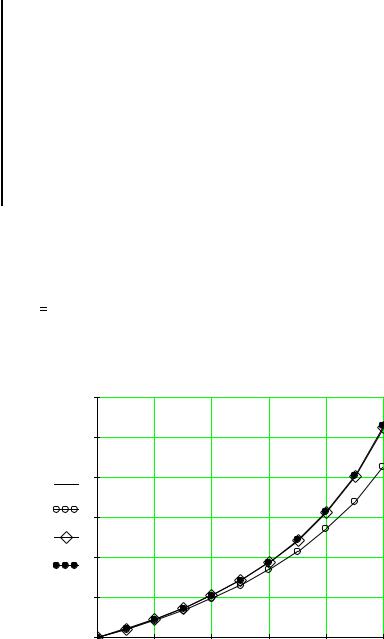
Побудуемо графіки отриманих розв’язків:

	4
	3.5
y(z)	3
	3
yE
yPK 2.5
yR	2
	2
	1.5
	1 0	0.1	0.2	0.3	0.4	0.5
				z x

<<< < Предыдущая 1 2 3 4 56 / 66

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.11.2018329.73 Кб6L7.doc
#
12.11.2018708.1 Кб17L9.doc
#
09.08.2019222.72 Кб4lab#1_AK.doc
#
25.08.2019562.69 Кб5Laboratorna_robota5.doc
#
23.02.2016119.81 Кб96Laboratorna_robota_6_Vkazivniki.doc
#
23.02.20162.05 Mб14Laboratorni_roboti_ChM.pdf
#
14.08.201995.74 Кб4Labs_вказивки.doc
#
23.02.2016268.8 Кб10Lab_1.doc
#
24.11.2019772.61 Кб2Lab_3_завдання.doc
#
23.02.2016118.87 Кб24Lab_bio_7_8.docx
#
23.02.201664.5 Кб155Lab_Rob_5_6.docx