Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Черкасский государственный технологический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Laboratorni_roboti_ChM

.pdf

Скачиваний:

Добавлен:

23.02.2016

Размер:

2.05 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 65 6 > Следующая >>>

Чисельні методи © Мірошкіна І.В.

	i	0	1		2		3	4

№ 12	x i	-2	-1		0		1	2

	f i	1.93	0.61		0.74		1.26	0.57
	f i	1.93	0.61		0.74		1.26	0.57

	~	-1.3		-0.3		0.3		1.3
	xi	-1.3		-0.3		0.3		1.3

	i	0	1		2		3	4

№ 13	x i	0	1		2		3	4

	f i	0.49	2.03		0.65		0.77	1.26
	f i	0.49	2.03		0.65		0.77	1.26
	~	0.85		1.85		2.85		3.85
	xi	0.85		1.85		2.85		3.85

	i	0	1		2		3	4

№ 14	x i	0	1		2		3	4

	f i	1.27	0.23		1.29		0.78	0.24
	f i	1.27	0.23		1.29		0.78	0.24
	~	0.53		1.53		2.53		3.53
	xi	0.53		1.53		2.53		3.53

	i	0	1		2		3	4

№ 15	x i	-2	-1		0		1	2

	f i	0.25	1.03		0.79		0.26	0.36
	f i	0.25	1.03		0.79		0.26	0.36
	~	-1.8		-0.8		0.8		1.8
	xi	-1.8		-0.8		0.8		1.8

	i	0	1		2		3	4

№ 16	x i	0	1		2		3	4
№ 16	f i	1.31	0.26		1.73		0.76	0.27
	f i	1.31	0.26		1.73		0.76	0.27
	~	0.25		1.25		2.25		3.25
	xi	0.25		1.25		2.25		3.25

	i	0	1		2		3	4

№ 17	x i	0	1		2		3	4

	f i	1.36	0.28		1.42		0.74	0.28
	f i	1.36	0.28		1.42		0.74	0.28

	~	0.85		1.85		2.85		3.85
	xi	0.85		1.85		2.85		3.85
				41

Чисельні методи © Мірошкіна І.В.

	i	0	1		2		3	4

№ 18	x i	-2	-1		0		1	2

	f i	1.35	0.29		1.45		0.74	0.34
	f i	1.35	0.29		1.45		0.74	0.34

	~	-1.47		-0.47		0.47		1.47
	xi	-1.47		-0.47		0.47		1.47

	i	0	1		2		3	4

№ 19	x i	-2	-1		0		1	2

	f i	1.37	0.31		1.52		0.75	0.33
	f i	1.37	0.31		1.52		0.75	0.33
	~	-1.51		-0.51		0.51		1.51
	xi	-1.51		-0.51		0.51		1.51

	i	0	1		2		3	4

№ 20	x i	0	1		2		3	4

	f i	1.44	0.33		1.55		0.66	0.77
	f i	1.44	0.33		1.55		0.66	0.77
	~	0.56		1.56		2.56		3.56
	xi	0.56		1.56		2.56		3.56

Звіт про виконання лабораторної роботи повинен містити:

-формулювання задачі;

-розрахунки в Mathcad;

-графічний аналіз результатів;

-висновки.

КОНТРОЛЬНІ ПИТАННЯ 24.Коли використовується інтерполяція функцій? 25.Що таке вузли інтерполяції?

26.Які інтерполюючі функції Ви знаєте?

27.Що таке сплайн-інтерполяція?

28.Що таке кубічний сплайн і як його побудувати? 29.Переваги і недоліки інтерполяції сплайнами.

30.З якими ще методами наближення функцій Ви знайомі?

Чисельні методи © Мірошкіна І.В.

ЗРАЗОК ВИКОНАННЯ ЛАБОРАТОРНОЇ РОБОТИ

Завдання: За допомогою програмного середовища Mathcad побудувати кубічний сплайн для

функції, що задана таблицею, і знайти його значення у вказаних точках x . Знайти розв’язок цієї ж задачі, використовуючи функції середовища Mathcad. Порівняти отримані розв’язки.

i	0	1		2		3	4

xi	-2	-1		0		1	2

fi	1.36	0.75		-1.21		0.33	-0.25
~	-1.3		-0.3		0.3		1.3
xi	-1.3		-0.3		0.3		1.3

Побудуємо чотири сплайн-функції (1) для кожного з інтервалів:

[ 2; 1] −					S ( x ) a b ( x x ) c ( x x )2 d															0	( x x )3 ;
						0			0	0		0			0		0			0			0
[ 1;0 ]	−		S		1	( x ) a			b ( x x			) c			( x x		)2 d		1	( x x				)3	;
					1		1			1	1		1			1			1			1
[ 0;1]	−	S	2	( x ) a			2	b		( x x	2	) c	2	( x x		2	)2 d	2		( x x			2	)3	;
			2				2		2		2		2			2		2					2
[1;2 ]	−	S	3	( x ) a			3	b		( x x	3	) c	3	( x x		3	)2 d	3		( x x		3		)3 .
			3				3		3		3		3			3		3				3

Знаходимо коефіцієнти сплайн-функцій за формулами (3), використовуючи програмне середовище Mathcad. Уведемо початкові дані: значення інтерполяційних вузлів (вектор x), значення функції у вузлах (вектор y), значення точок, у яких інтерполюється функція, (вектор z).

	2			1.36					1.3
	1			0.75					1.3
	1			0.75					0.3
x	0		f	1.21		z			0.3
x	0		f	1.21		z			0.3
									0.3
	1			0.33
									1.3
	2			0.25
Знаходимо коефіцієнти ai i 0,..., n 1 :
								1.36
i 0 3			ai fi		a			0.75
i 0 3			ai fi		a		1.21
							1.21

								0.33
Для знаходження коефіцієнтів сi		i 0,..., n потрібно скласти систему лінійних алгебраїч-

них рівнянь, яку розв’яжемо за допомогою спеціального обчислювального блоку Mathcad

Given/Find:

						4	1	0
i 0 4	ci 0		F			1	4	1	i 0 2	gi 3 fi 2 2 fi 1 fi

						0	1	4		0
										0
		c1								1.948

Given	F	c2			g	c Find(c)			c	3.744


										2.526
		c3								2.526

										0
Знаходимо коефіцієнти di , bi				i 0,..., n 1 , де h – крок між вузлами інтерполяції:

h 1
d3	c3		i 0 2	di	ci 1 ci
	3	h			3	h

i 0 3	bi	fi 1 fi	h	ci 1	2 ci
		h	3

Чисельні методи © Мірошкіна І.В.

			0.649

	d		1.897
	d		2.09
			2.09

			0.842
			0.039

	b		1.909
	b		0.114
			0.114

			1.104

Тепер можемо записати сплайн-функції для кожного інтервалу:

[ 2; 1]		− S0 ( x ) 1.36 0.039( x 2 ) 0.649( x 2 )3 ;
[ 1;0 ]		−	S		1	( x ) 0.75	1.909( x 1) 1.948( x 1)2 1.897( x 1)3	;
					1
[ 0;1]	−	S	2	( x ) 1.21			0.114x 3.744x2 2.09x3 ;
			2
[1;2 ]	−	S3 ( x ) 0.33 1.104( x 1 ) 2.526( x 1 )2 0.842( x 1 )3 .						(*)

Використовуючи отримані сплайни знайдемо значення функції f(x) у заданих точках:

			1.165
i 0 3	Si ai bi zi xi ci zi xi 2 di zi xi 3	S	0.89
i 0 3	Si ai bi zi xi ci zi xi 2 di zi xi 3	S	0.964
			0.964

			0.457

Знайдемо розв’язок цієї ж задачі, використовуючи функції середовища Mathcad.

v lspline(x f) y(t) interp(v x f t)

			1.5
			1.3
			1.1
			0.9
			0.7
			0.5
			0.3
f			0.1
			0.1
y( t)	2	1.2	0.4 0.1	0.4	1.2	2
			0.3
			0.5
			0.7
			0.9
			1.1
			1.3
			1.5

x t

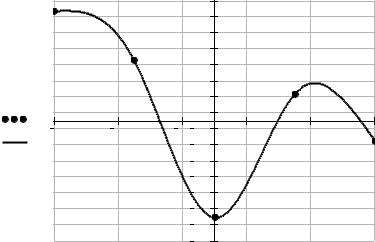
Тут функція interp(v,x,f,t) апроксимує дані векторів x і f кубічними сплайнами. v – вектор других похідних, створений функцією lspline(x,f), яка спирається на умову (2). Із графіку видно, що побудований сплайн y(t) у вузлах інтерполяції приймає задані значення

y( ti ) f ( xi ),

ti xi , i 0,1,..., n .

Порівняємо графіки і значення отриманих сплайн-функції (*) з функцією y(t) на кожному інтервалі.

i 0 3	S(i t) a	i	b	t x	c	t x	2	d	t x	3
		i	i	i	i	i		i	i

Чисельні методи © Мірошкіна І.В.

інтервал [ 2; 1] :

											1.5
											1
f											0.5
											0.5
y( t)
2.1	2	1.9	1.8	1.7	1.6	1.5	1.4	1.3	1.2	1.1	1
S(0 t)											0.5
											1
											1.5
						x t
інтервал [ 1;0 ] :
											1.5
											1
f											0.5
											0.5
y( t)
	1.1	1	0.9	0.8	0.7	0.6	0.5	0.4	0.3	0.2	0.1	0
S(1 t)											0.5
											1
											1.5

x t

інтервал [ 0;1] : 1.5

1.51

f	10.5
f y( t)	10.5
f y( t)	00..51	0	0.1	0.2 0.3		0.4	0.5 0.6		0.7	0.8	0.9	1
	00..51	0	0.1	0.2 0.3		0.4	0.5 0.6		0.7	0.8	0.9	1
S(2 t)	0.5
y( t)
	0.1	0	0.1	0.2	0.3	0.4	0.5	0.6	0.7	0.8	0.9	1
S(2 t)	0.5	1
	11.5
	1.5						x t
	1.5

x t

інтервал [1;2 ] :

1.5

f 0.5

y( t)

0.9

1.1

1.2

1.3

1.4

1.5

1.6

1.7

1.8

1.9

S(3 t) 0.5

1.5

x t

y( 1.3) 1.165 S(0 1.3) 1.165

y( 0.3) 0.89 S(1 0.3) 0.89

y(0.3) 0.964 S(2 0.3) 0.964

y(1.3) 0.457 S(3 1.3) 0.457

Як бачимо, побудовані сплайн-функції (*) мають повне співпадання з функцією y(t). Отже, задача розв’язана коректно.

Чисельні методи © Мірошкіна І.В.

ЛАБОРАТОРНА РОБОТА № 7

ТЕМА: Чисельне інтегрування.

МЕТА: Опанувати чисельними методами обчислення визначених однократних інтегралів за формулами лівих, правих, середніх прямокутників, трапецій, Сімпсона.

ТЕОРЕТИЧНІ ВІДОМОСТІ

Якщо функція f(x) – неперервна на відрізку [a,b] і відома її первісна функція F(x), то визначений інтеграл від цієї функції у границях від а до b може бути обчислений за формулою Ньютона-Лейбниця:

b
I	f ( x )dx F( b ) F( a ), де	F (x) f(x)..	(1)

Але в багатьох випадках первісна функція F(x) не може бути знайдена, або є дуже складною. Крім того, підінтегральна функція f(x) може бути задана таблично, тоді поняття первісної функції взагалі втрачає сенс. Постає задача наближеного обчислення інтегралів за допомогою чисельних методів.

Усі чисельні методи обчислення інтегралів базуються на геометричній інтерпретації визначеного інтеграла, значення якого чисельно дорівнює площі фігури, що обмежена зверху – графіком функції f(x), знизу – віссю 0х, зліва та справа – межами інтегрування a, b. Для знаходження площі відрізок [a,b] роз-

бивають на n рівних частин довжиною h, де	h b a	. Значення n обирають,
	n

виходячи з умови задоволення точності обчислень. Значення інтеграла I шукають як суму елементарних площадей фігур, що побудовані на інтервалах

[ xi , xi h ] .

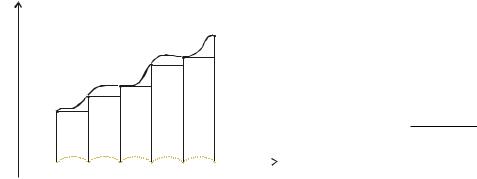
Метод лівих прямокутників. Апроксимуємо площі елементарних криволінійних трапецій, обмежених зверху графіком функції f(x), площами прямокутників, висота яких дорівнюватиме значенню f(x) у лівому кінці інтервалу [ xi , xi h ] (рис. 1). Загальну площу фігури обчислимо, як суму площ окремих

елементарних прямокутників:

y	n 1	b a n 1		b a n 1

y=f(x)	I Si		yi		f ( xi ).	(2)
		n		n
	i 0		i 0		i 0

Точність формули лівих прямокутників можна оцінити так:

	y0	y1	y2		yn			( b a )2	(3)
								f ( ),	(3)
	h	h	h	h	h			2n
	h	h	h	h	h		де [ a,b ] - точка, в якій перша похідна
0	a=x0	x1	x2		xn=b	x	де [ a,b ] - точка, в якій перша похідна
0	a=x0	x1	x2		xn=b	x
			Рис. 1				функції f(x) набуває найбільшого за моду-
			Рис. 1				лем значення.
							лем значення.

Блок-схема методу лівих прямокутників приведена на рис. 6.

Чисельні методи © Мірошкіна І.В.

Метод правих прямокутників. Апроксимуємо площі елементарних криволінійних трапецій, обмежених зверху графіком функції f(x), площами прямокутників, висота яких дорівнюватиме значенню f(x) у правому кінці інтервалу [ xi , xi h ] (рис. 2). Загальну площу фігури обчислимо, як суму площ окремих

елементарних прямокутників:

y
					y=f(x)
	y0	y1	y2		yn
	h	h	h	h	h
0	a=x0	x1	x2		xn=b	x

n	b a	n	b a	n
I Si		yi		f ( xi ).	(4)
	n		n
i 1		i 1		i 1

Точність формули правих прямокутників можна оцінити за формулою (3).

Рис. 2 Блок-схема методу правих прямокутників приведена на рис. 7.

Метод середніх прямокутників. Апроксимуємо площі елементарних криволінійних трапецій, обмежених зверху графіком функції f(x), площами прямо-

кутників, висота	яких дорівнюватиме	значенню		f(x) у			середині інтервалу
[ xi , xi h ] - yi 1	f ( xi h ) f ( xi 1	) (рис. 3). Загальну площу фігури об-
	2	2
числимо, як суму площ окремих елементарних прямокутників:
		n 1	b a n 1
y	I	Si		y	i	1
	I	Si	n	y		1
		i 0	n	i 0			2
		i 0		i 0

						y=f(x)
				y1+21
	y0+21
	y0		y1		y2	yn
	h		h
	2	2
0	a=x0	x0+21	x1	x1+21	x2	xn=b	x
					Рис. 3

b a n 1		h
	f ( xi		).	(5)
n	f ( xi	2	).	(5)
n	i 0	2
	i 0

Точність формули середніх прямокутників можна оцінити так:

( b a )3			(6)

24n	2	f ( ),

де [ a,b ] - точка, в якій друга похідна

функції f(x) набуває найбільшого за модулем значення.

Блок-схема методу середніх прямокутників приведена на рис. 8.

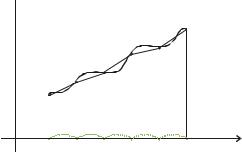
Метод трапецій. Апроксимуємо площі елементарних криволінійних трапецій, обмежених зверху графіком функції f(x), площами трапецій, висота яких

y=f(x)

	y0			y1		y2		yn




		h		h		h	h	h

0	a=x0		x1		x2			xn=b	x

Рис. 4

дорівнюватиме h, а довжини основ значенням f(x) у правому й лівому

кінцях	інтервалу [ xi , xi h ] -
f ( xi ) й	f ( xi h )(рис. 4). Загаль-

ну площу фігури обчислимо, як суму площ окремих елементарних трапецій:

n 1

b a y

I Si

y1 ... yn 1

i 0

b a

f ( x0

)

f ( x1 ) ... f ( xn 1 )

Точність формули трапецій можна оцінити так:

yn 2

f ( x	n	)
	n		.	(7)
			.	(7)
2

( b a )3		f ( ),	(8)
12n	2

де [ a,b ] - точка, в якій друга похідна функції f(x) набуває найбільшого за

модулем значення.

Блок-схема методу трапецій приведена на рис. 9.

Метод Сімпсона. Апроксимуємо площі елементарних криволінійних трапецій, обмежених зверху графіком функції f(x), площами криволінійних трапе-

y							цій, обмежених зверху параболою, що
							цій, обмежених зверху параболою, що
				y=f(x)			проходить через три точки ( x2i , y2i ),
				y=f(x)
							( x2i 1 , y2i 1 ) , ( x2i 2 , y2i 2 ) , i 0,1,...,n
							(рис. 5). Кількість точок для формули
	y2	y	y4	y			Сімпсона має бути завжди парною -
y1		y	y4	y			n 2m . Загальну площу фігури обчис-
y1		3			2m		n 2m . Загальну площу фігури обчис-
		3			2m
y0
h							лимо, як суму площ окремих елемента-
0 a=x0	x2		x4	x2m=b		x	рних криволінійних трапецій:

Рис. 5

n 1

b a

( y0 y2m ) 4( y1

... y2m 2 )

I Si

y3 ... y2m 1 ) 2( y2 y4

i 0

f ( x0 )

f ( x2m

) 4 f ( x1 ) ...

f ( x2m 1 ) 2 f ( x2 ) ...

f ( x2m 2 ) (9)

Точність формули Сімпсона можна оцінити так:

( b a )5

f IV ( ),

(10)

180n

де [ a,b ] - точка, в якій четверта похідна функції f(x) набуває найбільшого

за модулем значення.

Блок-схема методу Сімпсона приведена на рис. 10.

ЗАВДАННЯ

6.Методами прямокутників, трапецій та Сімпсона обчислити значення інтеграла з точністю 0,0001. Значення n обрати 10.Обчислити інтеграл засо-

бами Mathcad, обчислити похибку для кожного методу. Номер варіанта відповідає номерові завдань.

1.		0,8															16.		0,6												dx
			x cos xdx																												dx


																													1 x 4
			0																0										1 x 4
2.			0,6								dx						17.				0,3							e			x
			0,5								dx										0,1							e						dx

								1 x9																				x 2
3.																	18.		0 ,5
	0,5						1 x					4
	0,5											4													1 x 3 dx
																dx
									x 2							dx
	0,1								x 2										0
4.	3																19.				1,0								e		x
	3																												e				dx
	3				3
			x		3		arctg( x )dx																							x
			x				arctg( x )dx														0 ,1									x
	0
5.	0,5										dx						20.		0 ,25											x			2
	0,5																		0 ,25
																										e											dx

									1 x4
			0						1 x4												0
6.																	21.		0,5												dx
			4 cos x																												dx
			4 cos x
												dx														1 x												4
									x																													4
																					0
		6																			0
		6
7.	0 ,8			x10 sin xdx													22.		0,2								e			x
																											e								dx
																																			dx
	0																				0 ,1 x 3
8.	0 ,5																23.		1,0					cos x
8.	0 ,5						1 x 5 dx										23.		1,0
																																				dx
																																				dx
	0																		0,1											x
	0																		0,1

9.			1,0				sin x										24.		1,0
							sin x					dx												x sin xdx
												dx

			0,1								x								0
10.	1,0										dx						25.		1		3										dx
											dx										3



									2 x					4
			0											4														1 x											3
			0																0																				3
																			0
11.	1	3								x							26.								sin x
		3								x		2									2				sin x
			3									2			dx															x							dx

	0						1 x												4
	0						1 x												4
12.	1,0																27.		1,0
12.			cos x 2 dx														27.						x cos xdx
			cos x 2 dx																				x cos xdx
			0																0
13.		1,0				sin x 2 dx											28.	1,6	sin( 2x 2,1 )
																			sin( 2x 2,1 )																					dx
																																								dx
			0															1,2				x 2									1
14.	1,2						cos x										29.	1,0
14.													dx				29.			x 1 cos x 2 dx


	0,4					x 2					1							0,2
15.	1,2						cos x										30.		1,2						tgx							2
							cos x						dx												tgx												dx
													dx																								dx
	0,8					x 2 1													0,5						x 1
																	50

<<< < Предыдущая 1 2 3 45 / 65 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.11.2018329.73 Кб6L7.doc
#
12.11.2018708.1 Кб17L9.doc
#
09.08.2019222.72 Кб4lab#1_AK.doc
#
25.08.2019562.69 Кб5Laboratorna_robota5.doc
#
23.02.2016119.81 Кб96Laboratorna_robota_6_Vkazivniki.doc
#
23.02.20162.05 Mб14Laboratorni_roboti_ChM.pdf
#
14.08.201995.74 Кб4Labs_вказивки.doc
#
23.02.2016268.8 Кб10Lab_1.doc
#
24.11.2019772.61 Кб2Lab_3_завдання.doc
#
23.02.2016118.87 Кб24Lab_bio_7_8.docx
#
23.02.201664.5 Кб155Lab_Rob_5_6.docx