Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Черкасский государственный технологический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Laboratorni_roboti_ChM

.pdf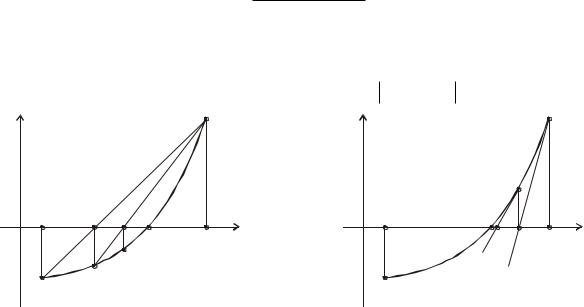

Скачиваний:

Добавлен:

23.02.2016

Размер:

2.05 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

Чисельні методи © Мірошкіна І.В.

В методі половинного ділення (рис. 2) інтервал відокремлення кореня [ a;b ]

ділять навпіл і в серединну точку c	a b	переміщують той кінець інтервалу

2

(a чи b), в якому знак функції збігається зі знаком f ( c ). Процес ділення продо-

вжують то тих пір, поки не виконається умова	f ( c )	або	b a	, де -

точність.

У методі січних ділення відрізку [ a;b ] відбувається пропорційно значенню функції в точках a та b (рис. 3). В цьому випадку точка поділу відрізка буде знаходитися на перетині хорди AB із віссю 0x, а її абсциса x1 є першим наближеним значенням кореня. Щоб уточнити x1 , застосуємо метод хорд до відрізка

[ x1 ;b ] ,

отримаємо друге наближення - x2 , і так далі. Нерухомим буде той кі-

нець відрізка ізоляції кореня, в якому знак функції f ( x )

збігається зі знаком

другої похідної.

Розрахункова формула методу січних:

xn 1

f ( xn )

( xn ),

(3)

f ( xn )

f ( )

де a , x0

b ,

якщо f ( a ) f ( a ) 0 ;

b ,

a ,

якщо f ( b ) f ( b ) 0 .

Розрахунки продовжують до виконання умови

xn 1 xn .

y=f(x)

f(x1)

x1 x2

f(x2)

f(x1)

Рис. 3

f ( x )

Рис. 4

У методі Ньютона ділянка кривої y

послідовно замінюється її дотич-

ною в точці A або B (рис.4). Абсциса точки перетину дотичної з віссю 0x - x1 буде першим наближеним значенням кореня. Щоб уточнити x1 застосуємо метод дотичних до відрізка [ a; x1 ] , отримаємо друге наближення - x2 , і так далі. Точка, в якій будується дотична, обирається з умови співпадання знаків функції та її другої похідної f ( x ) f ( x ) 0 .

Розрахункова формула методу Ньютона:
	xn 1 xn	f ( xn )		,	(4)
	xn 1 xn	f	( xn )	,	(4)
		f	( xn )
де x0 a , якщо	f ( a ) f ( a ) 0 ;
x0 b , якщо	f ( b ) f ( b ) 0 .
			21

Чисельні методи © Мірошкіна І.В.

Розрахунки продовжують до виконання умови xn 1 xn .

Модифікований метод Ньютона доцільно застосовувати, якщо похідна складно обчислюється:

n 1

f (xn )

(5)

f (x0 )

методі

простої ітерації

для

отримання

ітераційної формули, рівняння

f ( x ) 0

представляють у вигляді

x ( x ). Вибравши початкове наближення

a , будують ітераційний процес x1 ( x0

) , x2 ( x1 ) , …, до тих пір, по-

. Умовою збіжності ітераційного проце-

ки не виконається умова

xn 1

су являється дотримання нерівності ( x ) 1. Чим менше ( x ) , тим швидша збіжність. Як правило,

( x ) x

f ( x )

(6)

де q max

f ( x )

. Знак q має збігатися зі знаком

f ( x ) на [ a;b ] .

[ a;b ]

Система двох нелінійних рівнянь має вигляд:

F (x, y) 0,

(7)

G(x, y) 0.

Початкове наближення коренів

x0 , y0

визначають графічно. Для знаходження

наступних наближень використовують співвідношення методу Ньютона:

F (x

, y

)

, y

)

G(x

, y

) G

, y

)

xn 1 xn

J (xn , yn )

Fx (xn , yn )

Fy (xn , yn )

, y

)

, y

)

(8)

Fx (xn , yn )

F (xn , yn )

yn 1 yn

Gx (xn , yn ) G(xn , yn )

(xn , yn )

J (xn , yn )

, y

)

, y

)

, y

)

F (x

, y

)

Визначник

J (xn , yn )

називається Якобіаном системи

, y

)

, y

)

(7) і має бути відмінним від 0. Метод Ньютона вимагає достатньої близькості початкового наближення x0 , y0 до розв’язку.

Метод ітерацій. Систему (7) представляють у вигляді:

x (x, y),

(9)y (x, y).

Чисельні методи © Мірошкіна І.В.

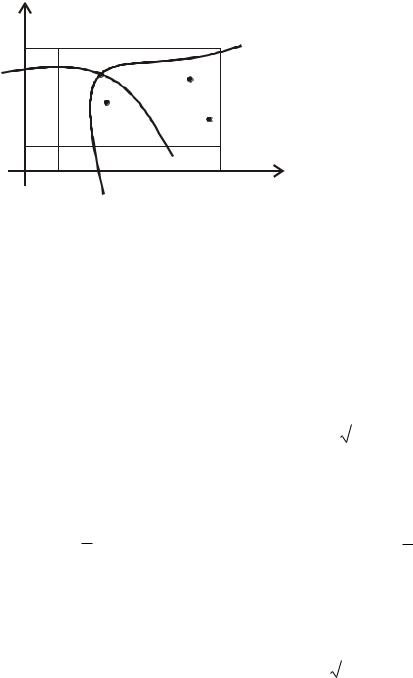
Нехай один із розв’язків системи (7) x , y належить деякій області D :{a x A, b y B} (рис. 5). Для уточнення розв’язку використовуємо формули:

x1 (x0 , y0 );	x2 (x1, y1);	… xn 1 (xn , yn );	…	(10)
y1 (x0 , y0 );	y2 (x1, y1);	yn 1 (xn , yn );

Початкове наближення x0 , y0

визначають графічно, і вони мають належати об-

ласті D. Ітераційний процес збігається, якщо в області D виконуються умови:

(11)

G(x,y)

( , )

F(x,y)

(x1,y1)

(xn,yn)

(x0,y0)

Рис. 5

ЗАВДАННЯ І. Відокремити корені нелінійного рівняння графічним методом. Уточнити

відокремлені корені з точністю 10 3				методами половинного ділення; Нью-
тона, модифікованим Ньютона, січних, простої ітерації.
Номер варіанта відповідає номерові рівняння.
1.	x sin( x ) 0,25			16.	x 2 2 sin( x ) 0,				x 0
2.	x 2		sin( 5x ) 0, x 0	17.	x cos( x )
		2	cos( x ) 0		2		cos	x 0
3.	x	2		18.	2	x	cos	x 0
3.	x			18.
								2

4.x 3 cos 2 ( 1,04x ) 0

5. 2 x 2x 2 1 0, x 0

6.2 ln( x ) 1x 0

7.3x3 8x 2 4x 8 0

8.x 0,5 x 1

9. x 2 cos( x ) 0,

x 0

10.5x 8 ln( x ) 8 0

11.x ln( x ) 0,5

12.2 x ln( x )

19.2,2x 2 x 0

20.2 x 4x 0

21.2 ln( x ) 2x 1 0

22.2 xe x 0

23.e x 2 x 1

24.	tg( x ) x, x 0
			1
25.		x 1
			x

26.	x ln( x ) 100
27.	xtg( x ) 1,28,			x 0

				Чисельні методи © Мірошкіна І.В.
13.	x e x e 3 x 4,	x 0	28.	ln( x ) tg( x ), x
13.	x e x e 3 x 4,	x 0	28.	ln( x ) tg( x ), x	2
					2
14.	6 x 5 sin( x ) 6,	x 0	29.	x4 x3 2x 5 0
15.	x5 2x 4 0		30.	3x 4 ln( x ) 5 0
	ІІ. Розв’язати систему нелінійних рівнянь із точністю 10 3 методом

Ньютона і методом ітерацій. Графічним способом визначити початкове наближення коренів системи x0 , y0 . Для методу ітерацій дослідити виконання

достатньої умови збіжності ітераційного процесу. Зробити висновки стосовно швидкості збіжності обох методів.

Номер варіанта відповідає номерові рівнянь.

№			№
1.	sin( x 1 ) y 1,2;		2.	cos( x 1 ) y 0,5;

	2x cos y 2.			x cos y 3.
3.	sin x 2 y 2;		4.	cos x y 1,5;
		0,7.
	cos( y 1 ) x	0,7.		2x sin( y 0,5 ) 1.
5.	sin( x 0,5 ) y 1;		6.	cos( x 0,5 ) y 0,8;
		0.
	cos( y 2 ) x	0.		sin y 2x 1,6.
7.	sin( x 1 ) y 1,3;		8.	2 y cos( x 1 ) 0;

	x sin( y 1 ) 0,8.			x sin y 0,4.
9.	cos( x 0,5 ) y 2;		10.	sin( x 2 ) y 1,5;

	sin y 2x 1.			x cos( y 2 ) 0,5.
11.	sin( y 1 ) x 1,2;		12.	cos( y 1 ) x 0,5;

	2 y cos x 2.			y cos x 3.
13.	sin y 2x 2;		14.	cos y x 1,5;
		0,7.
	cos( x 1 ) y	0,7.		2 y sin( x 0,5 ) 1.
15.	sin( y 0,5 ) x 1;		16.	cos( y 0,5 ) x 0,8;
		0.
	cos( x 2 ) y	0.		sin x 2 y 1,6.
17.	sin( y 1 ) x 1,3;		18.	2x cos( y 1 ) 0;
		0,8.
	y sin( x 1 )	0,8.		y sin x 0,4.
19.	cos( y 0,5 ) x 2;		20.	sin( y 2 ) x 1,5;

	sin x 2 y 1.			y cos( x 2 ) 0,5.
21.	sin( x 1 ) y 1;		22.	cos( x 1 ) y 0,8;

	2x cos y 2.			x cos y 2.
23.	sin x 2 y 1,6;		24.	cos x y 1,2;

	cos( y 1 ) x 1.			2x sin( y 0,5 ) 2.
25.	sin( x 0,5 ) y 1,2;		26.	cos( x 0,5 ) y 1;
		0.
	cos( y 2 ) x	0.		sin y 2x 2.
27.	sin( x 1 ) y 1,5;		28.	sin( y 1 ) x 1;

	x sin( y 1 ) 1.			2 y cos x 2.

a 1 b 2

			Чисельні методи © Мірошкіна І.В.
29.	cos( y 1 ) x 0,8;	30.	cos( x 1 ) y 1;

	y cos x 2.		sin y 2x 1,6.

Звіт про виконання лабораторної роботи повинен містити:

-формулювання задачі;

-лістинг розрахунків в Mathcad;

-отримані чисельні результати;

-аналіз результатів;

-висновки.

КОНТРОЛЬНІ ПИТАННЯ

1.Що означає відокремити корені рівняння?

2.Які методи уточнення коренів нелінійних рівнянь Вам відомі?

3.Сутність методу половинного ділення. Пояснити на графіку.

4.Сутність методу січних. Пояснити на графіку.

5.Сутність методу Ньютона. Пояснити на графіку.

6.Сутність методу простої ітерації. Пояснити на графіку.

7.Сутність методу Ньютона для системи двох нелінійних рівнянь.

8.Наведіть ітераційну формулу метода Ньютона для системи n нелінійних рівнянь.

9.Як визначається Якобіан системи нелінійних рівнянь?

10.Сутність методу ітерацій.

11.Якими є умови збіжності методу ітерацій?

12.Наведіть ітераційну формулу метода ітерацій для системи n нелінійних рівнянь, порівняйте її з ітераційною формулою метода Ньютона.

ЗРАЗОК ВИКОНАННЯ ЛАБОРАТОРНОЇ РОБОТИ

І. Знайти розв’язок нелінійного рівняння з точністю 10 3 : x 0,5x 1.

Відокремимо корені рівняння графічним методом. Точка перетину графіка функції з віссю Ох буде наближеним значенням кореня. Ми вкажемо інтервал ізоляції кореня.

f(x) x 0.5x 1

		5
		4
		3
		2
		1
f(x)	5	4 3 2 1 0 1 2 3 4	5
	5	4 3 2 1 0 1 2 3 4	5
		1
		2
		3
		4
		5

Корінь рівняння знаходиться в інтервалі [a, b]

Задля контролю правильності розрахунків знайдемо розв’язок рівняння функцією Mathcad:

x 1 root(f(x) x) 1.38333

Чисельні методи © Мірошкіна І.В.

Метод половинного ділення

b a

a 1

c 1.5

b 2

f(a) 0.5

f(c) 0.146

f(b) 0.75 b c

b a

a 1

c 1.25

b 1.5

f(a) 0.5

f(c) 0.17

f(b) 0.146

a c

b a

a 1.25

c 1.375

b 1.5

f(a) 0.17

f(c) 0.011

f(b) 0.146

a c

b a

a 1.375

c 1.438

b 1.5

f(a) 0.011

f(c) 0.068

f(b) 0.146

b c

b a

a 1.375

c 1.406

b 1.438

f(a) 0.011 f(c) 0.029

f(b) 0.068

b c

b a

a 1.375

c 1.391

b 1.406

f(a) 0.011

f(c) 9.225 10 3

f(b) 0.029 b c

b a

a 1.375

c 1.383

b 1.391

f(a) 0.011

f(c) 6.58 10 4

f(b) 9.225 10 3

Відповідь : x=1.383;

кроків 7

Метод Ньютона

1 b 2

f1(x) d f(x)

f2(x)

f(x)

dx2

f(a) f2(a) 0.12

f(b) f2(b) 0.09

x0 a

x1 x0

f(x0)

f1(x0)

x1 1.3713

x1 x0

0.371

x2 x1

f(x1)

f1(x1)

x2 1.3833

x2 x1

0.012

x3 x2

f(x2)

x3 1.3833

x3 x2

1.055 10 5

f1(x2)

Відповідь : x=1.383;

кроків 3

Модифікований метод Ньютона

x0 a

x1 x0

f(x0)

f1(x0)

x1 1.3713

x1 x0

0.371

x2 x1

f(x1)

f1(x0)

x2 1.3826

x2 x1

0.011

x3 x2

f(x2)

x3 1.3833

6.692 10 4

f1(x0)

x3 x2

Відповідь : x=1.383; кроків 3

Метод січних

f2(x)

f(x)

f(a) f2(a) 0.12

f(b) f2(b) 0.09

x0 b

x1 x0

f(x0)

(x0 )

1.4

x1 x0

0.6

f(x0) f( )

x2 x1

f(x1)

(x1 )

1.3838

x2 x1

0.016

f(x1) f( )

x3 x2

f(x2)

(x2 )

1.3833

x3 x2

4.78 10 4

f(x2) f( )

Відповідь : x=1.383; кроків 3

Метод ітерацій

M 2

d f(x)

1.2

1.4

1.6

1.8

(x) x

f(x)

a b

x0 1.5

x1 (x0)

x1 1.4268

x1 x0

0.073

x2 (x1)

x2 1.3994

x2 x1

0.027

x3 (x2)

x3 1.3892

x3 x2

0.01

x4 (x3)

x4 1.3855

x3 x4

3.732 10 3

x5 (x4)

x5 1.3841

1.372 10 3

x5 x4

x6 (x5)

x6 1.3836

5.038 10 4

x6 x5

x7 (x6)

x7 1.3834

x7 x6

1.85 10 4

Відповідь : x=1.383; кроків 6

ІІ. Розв’язати систему нелінійних рівнянь з точністю 10 3 ітерацій:

sin( x 0.6 ) y 1.6;3x cos( y ) 0.9.

Метод Ньютона.

Приведемо систему до вигляду:

F (x, y) 0,	F (x, y) sin(x 0.6) y 1.6 0;
		0.9	0.
G(x, y) 0.	G(x, y) 3x cos(y)

методом Ньютона і методом

Знайдемо графічним способом початкове наближення коренів системи x0 , y0 . Для цього

побудуємо в Mathcad графіки функцій обох рівнянь.

З першого рівняння зручно визначити невідому y: y sin( x 0.6) 1.6 , а з другого – невідому x: x 13 cos( y) 0.3 . Тоді будуємо графіки.

						5
						5
						4
						4
						3
						3
						2
						2
sin(x 0.6) 1.6						1
						1

y	5	4	3	2	1		0	1	2	3	4	5
						1
						1
						2
						2
						3
						3
						4
						4
						5
						5

x 0.3 13 cos( y)

Визначаємо початкове наближення коренів системи (точка перетину обох графіків): x0 0.2 ; y0 2 .

Уточнення коренів системи проведемо за допомогою розрахунків в Mathcad:

F(x y) sin (x 0.6) y 1.6 G(x y) 3x cos(y) 0.9

J(x y)

x0 0.2

x1 x0

x2 x1

d F(x y)

d G(x y)

y0 2x(x0 y0) J(x0 y0)

x(x1 y1) J(x1 y1)

F(x y)

x (x y)

y (x y)

G(x y)

y1 y0

y (x0 y0)

J(x0 y0)

0.151

y1 2.035

x1 x0

0.049

y1 y0

0.035

y2 y1

y (x1 y1)

J(x1 y1)

0.151

y2 2.034

x2 x1

3.176 10 4

y2 y1

7.769 10 4

Відповідь: x=0.151, y=-2.034; кроків 2.

Метод ітерації.

Приведемо систему до вигляду:

x (x, y),

y (x, y).

Для цього з другого рівняння системи зручно визначити невідому x, а з першого - невідому y. Тоді маємо:

	1
x (x, y)		cos(y) 0.3;
x (x, y)		cos(y) 0.3;
	3

y (x, y) sin(x 0.6) 1.6.
Початкове наближення коренів системи визначили раніше: x0 0.2 ;			y0 2 .

Дослідимо виконання достатньої умови збіжності ітераційного процесу:

			1,				1.

x		x		y		y
	D		D		D		D

Задамо область D навколо x0 , y0 :

D { 0.1 x 0.3, -1.9 y -2.1}.

Обчислення значень похідних виконаємо в Mathcad:

(y)

0.3

cos(y)

(x) sin (x 0.6)

1.6

x 0.2

y 2.0

V(y)

(y)

W(x)

d (x)

Given

0.1 x 0.3

P Maximize(W x)

P 0.3

W(P) 0.955

1.9 y 2.1

M Maximize(V y)

M 1.571

V(M) 0.333 <1

Отримані значення похідних 0.955 і 0.333 менше 1, тобто умова збіжності виконується, ітераційний процес буде збіжним. Уточнимо корені системи в Mathcad.

x0 0.2

y0 2

x1 (y0)

y1 (x0)

x1 0.161

y1 1.989

x1 x0

0.039

y1 y0

0.011

3.215 10 3

x2 (y1)

y2 (x1)

x2 0.164

y2 2.025

x2 x1

y2 y1

0.035

2.913 10 3

x3 (y2)

y3 (x2)

x3 0.154

y3 2.022

x3 x2

0.011

y3 y2

8.732 10 4

9.66 10 3

x4 (y3)

y4 (x3)

x4 0.155

y4 2.032

x4 x3

y4 y3

2.891 10 3

7.879 10 4

x5 (y4)

y5 (x4)

x5 0.152

y4 2.032

x5 x4

y5 y4

2.353 10 4

2.607 10 3

x6 (y5)

y6 (x5)

x6 0.152

y6 2.033

x6 x5

y6 y5

x7 (y6)

y7 (x6)

x7 0.151

y7 2.033

x7 x6

7.783 10 4

y7 y6

2.121 10 4

Відповідь: x=0.151,

y=-2.033;

кроків 7.

ЛАБОРАТОРНА РОБОТА № 5

ТЕМА: Інтерполяція функцій.

МЕТА: Опанувати чисельними методами інтерполяції функцій поліномами Лагранжа та Ньютона.

				ТЕОРЕТИЧНІ ВІДОМОСТІ
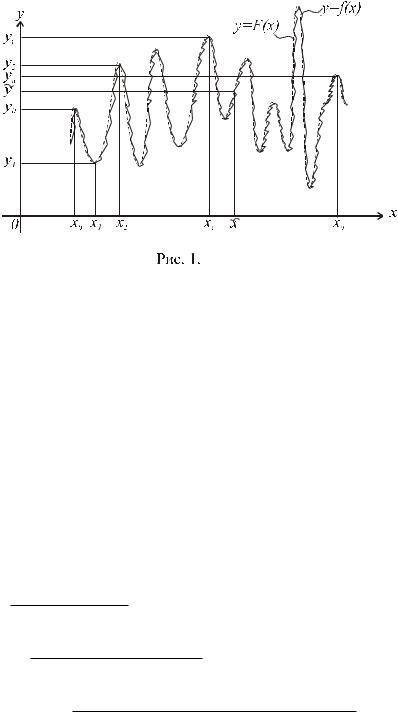
		Інтерполяцію функцій застосовують, коли деяка функція задана таблично
скінченою множиною x:				f ( x0 ) y0 , f ( x1 ) y1 ,..., f ( xn ) yn				і потрібно ви-
							~	~
значити значення f ( x ) для проміжних значень аргументу x -								f ( x ). В цьому
разі будують функцію F( x )						(достатньо просту для обчислень), яка в точках
{ x	i	}n	набуває значення	{ y	i	}n	. В інших точках F( x ) наближено представ-
	i	i 0			i	i 0

ляє функцію f ( x ) з тою чи іншою точністю (рис. 1).

Точки { x	i	}n		називають вузлами інтерполяції, функцію F( x ) - інтерпо-
	i	i 0
люючою функцією, а задачу побудови F( x ) - задачею інтерполяції.
Зазначені вище властивості інтерполюючої функції має поліном Лагран-
жа:				( x x0 )( x x1 ) ... ( x xi 1	)( x xi 1 ) ... ( x xn )
n				( x x0 )( x x1 ) ... ( x xi 1	)( x xi 1 ) ... ( x xn )
Ln ( x ) yi						.
Ln ( x ) yi			( xi x0 )( xi x1 ) ... ( xi xi 1		)( xi xi 1 ) ... ( xi xn )	.
i 0			( xi x0 )( xi x1 ) ... ( xi xi 1		)( xi xi 1 ) ... ( xi xn )

Поліном Лагранжа незручний у використанні тим, що при зміні кількості вузлів інтерполяції n, його треба будувати знову.

Інтерполяційний поліном Ньютона не має цього недоліку. При зміні степеня n необхідно лише тільки додати або відкинути відповідну кількість стандартних доданків:

Pn (x) f (x0 ) (x x0 ) f (x0 ; x1 ) (x x0 )(x x1 ) f (x0 ; x1 ; x2 ) ...(x x0 )(x x1 ) ... (x xn 1 ) f (x0 ; x1 ; x2 ;...; xn ).

Тут f ( x0 ; x1 ) f ( x1 ) f ( x0 ) - розділена різниця першого порядку; x1 x0

f ( x0 ; x1 ; x2 ) f ( x1 ; x2 ) f ( x0 ; x1 ) - розділена різниця другого порядку; x2 x0

f ( x0 ; x1 ; x2 ...; xn ) f ( x1 ; x2 ;...; xn ) f ( x0 ; x1 ;...; xn 1 ) - розділена різниця xn x0

n-ого порядку.

Часто інтерполювання необхідно проводити для функції, що задана у рівновіддалених вузлах, тобто:

h xi 1 xi const ( i 0,1,...,n ) .

Для таких таблиць інтерполяційні формули значно спрощуються.

а) перша інтерполяційна формула Ньютона:

P ( x ) P ( x

ih ) y

q( q 1 )

...

q( q 1 ) ... ( q

n 1 )

;

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
12.11.2018329.73 Кб6L7.doc
#
12.11.2018708.1 Кб17L9.doc
#
09.08.2019222.72 Кб4lab#1_AK.doc
#
25.08.2019562.69 Кб5Laboratorna_robota5.doc
#
23.02.2016119.81 Кб96Laboratorna_robota_6_Vkazivniki.doc
#
23.02.20162.05 Mб14Laboratorni_roboti_ChM.pdf
#
14.08.201995.74 Кб4Labs_вказивки.doc
#
23.02.2016268.8 Кб10Lab_1.doc
#
24.11.2019772.61 Кб2Lab_3_завдання.doc
#
23.02.2016118.87 Кб24Lab_bio_7_8.docx
#
23.02.201664.5 Кб155Lab_Rob_5_6.docx