Література до теми Основна

1. Ситник В. Ф., Орленко Н. С. Імітаційне моделювання: Навч. посібник. — К.: КНЕУ, 1998. — С. 65—76.

2. Сытник В. Ф. Основы машинной имитации производственних и организационно-экономических систем. — К.: УМК ВО, 1988.  С. 65—78.

Допоміжна

3. Клейн Дж. Статистические методы в имитационном моделировании. — М.: Статистика, 1978. —Т.1. — С. 30—34.

4. Нейлор Т. Машинные имитационные эксперименты с моделями экономических систем. — М.: Мир, 1975. — С. 388—392.

5. Шеннон Р. Имитационное моделирование систем — искусство и наука. — М.: Мир, 1978. — С. 388—397.

6. Харин Ю. С., Малюгин В. И., Кирлица В. П. и др. Основы имитационного и статистического моделирования: Учеб. пособие.  Минск: Дизайн ПРО, 1997.  С. 86—95.

7. Ермаков С. М. Метод Монте-Карло и смежные вопросы. — М.: Наука, 1975. — С. 39—80.

8. Ермаков С. М., Михайлов Г. А. Статистическое моделирование. — М.: Наука, 1982. — С. 17—36.

8.2. Практичне заняття

Мета заняття: Перевірити розуміння сутності й необхідності розробки методів імітації на ЕОМ неперервних випадкових величин. Набути навички застосовування різних методів та їх модифікацій для реалізації в складі імітаційної моделі випадкових параметрів, які мають різні неперервні функції розподілу.

План

1. Стандартний метод імітації неперервних випадкових величин.

2. Метод добору (відбракування) неперервних випадкових величин.

3. Наближене формування розподілів неперервних випадкових величин.

4. Генерування нормально розподілених випадкових величин.

8.3. Термінологічний словник

Неперервна випадкова величина — випадкова величина X, яка може приймати будь-які значення з деякого замкненого або відкритого інтервалу, в тому числі і нескінченного. Функція розподілу її є неперервною функцією. Якщо існує невід’ємна функція, така, що для всіх, тоназивається щільністю ймовірностей випадкової величини.

Експоненціальний розподіл має щільність ймовірностей та функцію розподілу такого виду:

Математичне сподівання експоненціально розподіленої випадкової величини дорівнює , а дисперсія —. Цьому закону розподілу підпорядковуються багато явищ: тривалість телефонних розмов, термін служби багатьох електронних деталей, час надходження замовлень на підприємства обслуговування, час прибуття літаків до аеропорту тощо.

Нормальний розподіл — найважливіший в теорії ймовірностей закон розподілу ймовірностей. Випадкова величина X має нормальний розподіл з параметрами і, якщо щільність розподілу ймовірностей має вигляд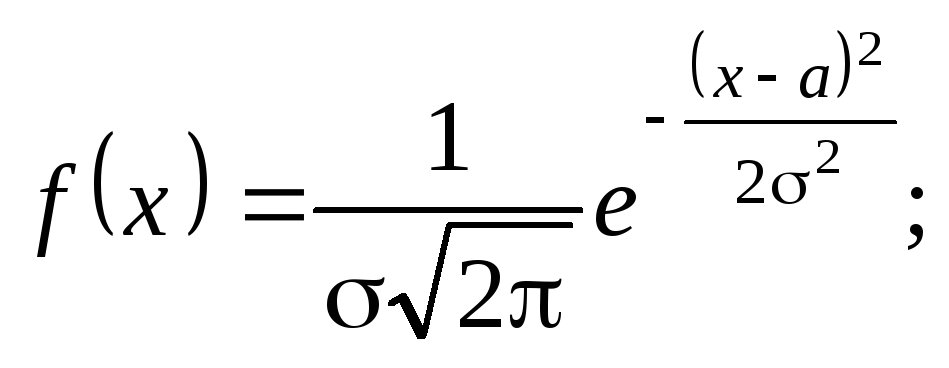де— математичне сподівання випадкової величиниX; — її дисперсія.

Центральна гранична теорема — теорема, що встановлює умови, за яких розподіл імовірностей суми великої кількості незалежних доданків близький до нормального розподілу. Для однаково розподілених доданків такою достатньою умовою є те, щоб доданки мали обмежену, відмінну від нуля дисперсію. Центральна гранична теорема може бути застосована і до суми випадкових величин, які мають неоднаковий розподіл. У такому разі вимагається, щоб серед доданків не було таких, які б впливали на загальну суму більше, ніж решта її складових.

8.4. Навчальні завдання

Вправа 1. До порту заходять танкери для завантаження нафтою, інтервал часу (в годинах) між появою танкерів — рівномірно розподілена випадкова величина на відрізку [4, 18]. Танкери можуть бути трьох типів: А, В, С. Скласти методом машинної імітації розклад прибуття танкерів, якщо ймовірності їх появи відповідно дорівнюють 0,25, 0,55, 0,20.

Вправа 2. Згенеруйте ряд значень експоненціально розподіленої випадкової величини, якщо інтенсивність однорідного потоку, що описується цією випадковою величиною, дорівнює  = 5.

Вправа 3. За допомогою стандартного методу згенеруйте 4 реалізації випадкової величини, яка має розподіл Коші, щільність ймовірностей якого має вигляд

.

Вправа 4. Необхідно визначити розмір площі у центрі зайнятості для обслуговування безробітних, які приходять до центру згідно з пуассонівським законом розподілу ймовірностей. Середня інтенсивність дорівнює 2 особи на годину. Час виконання робіт, пов’язаний з обслуговуванням одного клієнта, є експоненціально розподіленою величиною з середнім значенням 0,4 години. Для розміщення однієї людини потрібно мати 1 м² площі. Скільки місця буде потрібно, щоб розмістити 90% людей, що знаходяться в черзі.

Вправа 5. Згенеруйте 5 нормально розподілених випадкових чисел з математичним сподіванням 6 і дисперсією 9, використовуючи табличний метод; метод, заснований на використанні центральної граничної теореми; метод Бокса–Маллера; метод Марсальї–Брея. Під час виконання вправи слід скористуватися таблицями Д. 1 і Д. 2 посібника [1].