
Algebra_i_geometriya / І модуль / NE_1.1 / Практичні заняття до НЕ 1
.1.docПриклади розв’язування задач
Приклад
1.
Обчислити
![]() .
.
Розв’язання
Оскільки
![]() ,
то
,
то![]()
Отже,
![]() .
.
Приклад
2.
Обчислити вираз
![]() .
.
Розв’язання
Спершу спростимо чисельник:



![]() .
.
Приклад
3. Розв’язати
рівняння, вважаючи
![]() та
та
![]() дійсними числами
дійсними числами
![]() .
.
Розв’язання
Перетворимо ліву частину рівняння, розкривши дужки та звівши дійсні і уявні доданки:

Отримали зліва і справа комплексні числа, які рівні тоді і тільки тоді, коли рівні одночасно їх дійсні і уявні частини. А тому рівняння (*) рівносильне системі рівнянь:

Розв’яжемо
дану систему, і знайдемо
![]() та
та
![]() .
Помноживши 1-ше рівняння системи на
.
Помноживши 1-ше рівняння системи на
![]() ,
а 2-ге на
,
а 2-ге на
![]() і додавши їх, отримаємо:
і додавши їх, отримаємо:

Звідки
![]() .
.
Виразимо
з другого рівняння
![]() :
:

Відповідь:
![]() .
.
Приклад
4. Розв’язати
систему
рівнянь, вважаючи
![]() та
та
![]() комплексними числами
комплексними числами

Розв’язання
Оскільки маємо систему із двох лінійних рівнянь з двома змінними, то спробуємо їх розв’язати за допомогою формул Крамера. Обчислимо спочатку головний визначник системи:
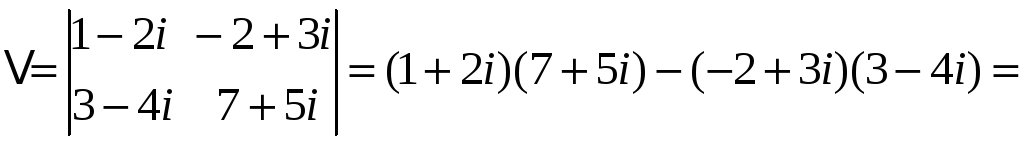
![]()
![]() .
.
Оскільки
![]() ,
то
,
то
![]() .
.

![]() .
.
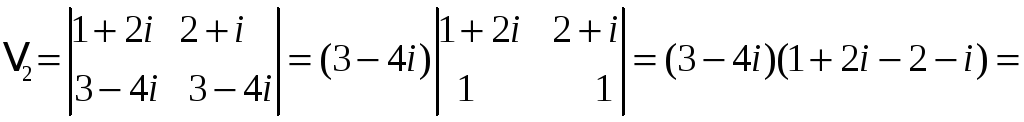
![]()
Підставимо
![]() і
і
![]() у формули Крамера і знайдемо
у формули Крамера і знайдемо
![]() та
та
![]() .
.
 .
.

![]() .
.
Відповідь:
![]() ,
,
![]() .
.
Приклад
5. Обчислити
![]() .
.
Розв’язання
Оскільки
корінь з комплексного числа, взагалі
кажучи, комплексне число (і не одне), то
подамо всі значення кореня у вигляді
![]() ,
де
,
де
![]() .
.
Тоді
![]() .
.
Піднесемо
обидві частини рівняння до квадрату і
знайдемо
![]() та
та
![]() .
.
![]()
Зліва і справа в останній рівності отримали комплексні числа, які рівні тоді, коли рівні їх дійсні і уявні частини. Тому рівняння (**) рівносильне системі

З другого рівняння маємо, що:
![]() .
.
Підставимо
![]() в перше рівняння і отримаємо:
в перше рівняння і отримаємо:
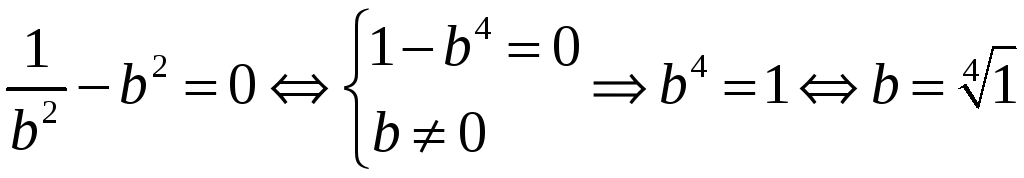 .
.
Оскільки
![]() ,
то
,
то
![]() або
або
![]() .
Тоді
.
Тоді
![]() або
або
![]() .
.
Тобто
отримали два значення
![]() :
:
![]() або
або
![]() .
.
Приклад
6. Розв’язати
рівняння, вважаючи
![]() комплексним числом
комплексним числом
![]() .
.
Розв’язання.
Маємо квадратне рівняння відносно
![]() з комплексними коефіцієнтами. Знайдемо
дискримінант рівняння:
з комплексними коефіцієнтами. Знайдемо
дискримінант рівняння:
![]() ,
,
тоді
 .
.
Знайдемо
значення кореня з комплексного числа
![]() ,
враховуючи міркування з прикладу 5.
,
враховуючи міркування з прикладу 5.
![]()

Розглянемо друге рівняння системи окремо:
![]()
Отримали
біквадратне рівняння відносно
![]() .
.
![]() ,
тоді
,
тоді

Тобто
 або
або
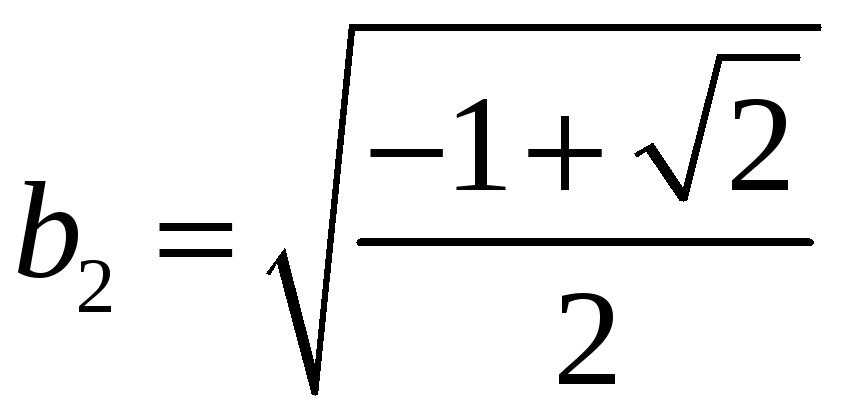 ,
,
тоді
 або
або
 .
.
Отже,
 ,
,
 .
.
Повернемось до коренів вихідного рівняння і матимемо:
 та
та
 .
.
Відповідь:
дане рівняння має два корені
 та
та
 .
.
Приклад
7. Знайти
число, спряжене до даного
![]() .
.
Розв’язання
![]() ,
тоді
,
тоді

Оскільки спряжене до частки чисел є часткою спряжених чисел, то

![]() .
.
Отже,
![]() .
.
Приклад
8. Зобразити
в тригонометричній формі число
![]()
Розв’язання
![]() ,
тоді
,
тоді
![]()
![]()
Приклад
9. Обчислити

Розв’язання. Подамо чисельник та знаменник дробу у тригонометричній формі:
![]() ,
,
![]() .
.
Тоді

![]()
![]()
Приклад
10. Обчислити
![]() .
.
Розв’язання. Подамо підкореневий вираз, який є комплексним числом, взагалі кажучи, у тригонометричній формі:
![]()
![]() ;
;
![]()
![]()
![]()
![]()
![]()

![]()


![]()

Очевидно,
що
![]()
Приклад
11. Виразити
![]() через
через
![]() .
.
Розв’язання.
 .
Щоб виразити
.
Щоб виразити
![]() та
та
![]() через
через
![]() та
та
![]() ,
використаємо формулу мавра та біном
Ньютона:
,
використаємо формулу мавра та біном
Ньютона:
![]()

![]()
![]()

Приклад 12. Виписати всі корені 6-го степеня із одиниці. Вказати первісні.
Розв’язання.
![]() ,
тоді
,
тоді
![]()
![]()


![]()

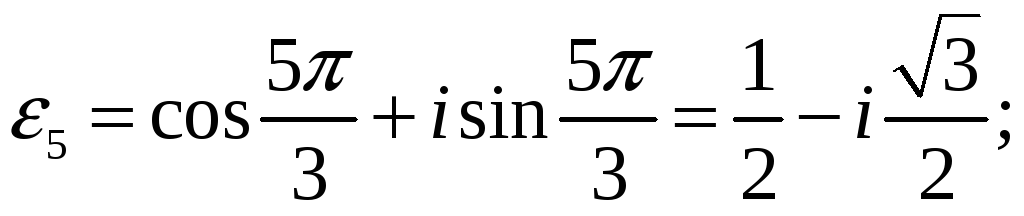
Первісні:
 ;
;
 .
.
Знайти
порядки
![]() і
і
![]() .
.
![]() –порядок
–порядок
![]()
![]()
![]()
![]()
![]()
![]() –порядок
6.
–порядок
6.

![]() –порядок
3.
–порядок
3.
