Тема 23: АЛГОРИТМИ ВИЗНАЧЕННЯ ВЛАСТИВОСТЕЙ БІНАРНОГО ДЕРЕВА

Враховуючи рекурсивність структури і впорядкованість елементів, вивід їх на екран здійснюватиме теж рекурсивна процедура за порядком зростання, за алгоритмом:

1.Здійснюватиметься рух по дереву до крайнього лівого елемента (найменшого).

2.Це значення друкується.

3.Робиться один крок вправо і послідовність 1-3 повторюється відносно нової поточної вершини.

Програмна реалізація алгоритму друку має вигляд процедури:

PROCEDURE OUTPUT (p:bintree); BEGIN

if p^.left<>nil then OUTPUT(p^.left); write(p^.inf,' ');

if p^.right<>nil then OUTPUT(p^.right); END;

Пошук елементу за вказаним значенням подібний до алгоритму виведення, при цьому замість процедури друку використовується порівняння інформаційних полів.

PROCEDURE FIND (p:bintree; x:integer); BEGIN

inc(i);

if p^.right<>nil then FIND(p^.right,x); if p^.inf=x then

begin

write('є під номером(ами) '); Str(i,d);

s:=s+d;

end;

if p^.left<>nil then FIND(p^.left,x);

if (p=top) and (s='') then writeln('елемент не знайдено'); END;

Щоб визначити ширину дерева достатньо здійснити рекурсивний рух вліво і вправо до кінця відносно вершини із підрахунком кількості кроків, а потім додати.

PROCEDURE MOVE_RIGHT(p:bintree); BEGIN

if p^.right<> nil then begin

k:=k+1; MOVE_RIGHT(p^.right) end;

END;

PROCEDURE MOVE_LEFT(p:bintree); BEGIN

if p^.left<> nil then begin

k:=k+1; MOVE_LEFT(p^.left) end;

END;

78

В основній програмі це буде мати вигляд:

n:=0;

k:=0; MOVE_RIGHT(top); MOVE_LEFT(top); writeln('ширина :',n+k+1);

Процедура визначення висоти бінарного дерева буде мати вигляд:

PROCEDURE HIGHT(p:bintree;k:integer); BEGIN

if p^.left<>nil then HIGHT(p^.left, k+1); if k>h then h:=k;

if p^.right<>nil then HIGHT(p^.right,k+1) END;

Для встановлення кількості висячих вершин використовують таку процедуру: PROCEDURE LUSTOK(p:bintree;var l:word);

begin

if (p^.left=nil) and (p^.right=nil) then inc(l); if p^.left<>nil then LUSTOK(p^.left,l);

if p^.right<>nil then LUSTOK(p^.right,l); end;

Доповнення новим елементом проводиться так само як формування дерева.

Складність видалення пов’язана із тим, що приходиться аналізувати декілька можливих ситуацій:

а). Видалення висячої вершини найбільш проста. Вона передбачає встановлення у nil вказівника на елемент, що видаляється, для цього потрібно мати фіксований вказівник на попередній елемент.

Dispose(p^.right);

p^.right:=nil;

Dispose(p^.left);

p^.left:=nil;

б). Видалення напіввисячої вершини. При цьому всі елементи, що знаходяться нижче елемента, що видаляється підтягуються на один рівень вверх.

79

Тема 24. ПОНЯТТЯ ГРАФА ТА ЙОГО ЗОБРАЖЕННЯ В ПАМ'ЯТІ КОМП'ЮТЕРА

Граф – це сукупність непорожньої множини V вершин і множини Е невпорядкованих або

прийнято називати початком дуги, а другу – її кінцем. Граф, що не містить дуг, називається неорієнтованим, а граф, що містить дуги – орієнтованим, або ортграфом. Ребро (дуга) і будьяка його (її) вершина називаються інцидентними. З’єднані ребром вершини називаються суміжними. Якщо вершина v є початком певної дуги, а вершина w – її кінцем, то вершину w вважають суміжною з вершиною v, але не навпаки.

Неорієнтований граф зображують на площині як сукупність точок, що відповідають вершинам, і як сукупність відрізків, що з’єднують точки та відповідають ребрам. Якщо граф містить дуги, вони зображуються стрілками, що з’єднують точки.

Для використання графів у програмуванні потрібно вибрати спосіб їх зображення в оперативній пам'яті. Найвідомішими структурами даних, що зображують графи, є матриці суміжності, матриці інциденцій, масиви дуг, списки суміжності.

Нехай n – кількість вершин графу, m – кількість його ребер, всі вершини графу

Рис.1. Орієнтований граф D та неорієнтований граф G. Матриця суміжності цих графів такі:

80

Основним недоліком зображення графу за допомогою матриць суміжності та інциденцій є те, що ці матриці містять O(n2) елементів навіть тоді, коли граф складається з O(n) вершин і O(n) ребер. Більшість алгоритмів на графах потребують перегляду кожного ребра графі принаймні один раз. Тому, якщо реалізувати певний алгоритм, що має часову складність O(n), з використанням матриць суміжності або інциденцій, його часова складність, як правило, зросте до O(n2).

У багатьох випадках економніший, з погляду ємнісних і часових витрат, спосіб зображення графу полягає у використанні списку суміжності. Кожен елемент такого списку посилається на наступний елемент, а також містить номер певної вершини і посилається на список суміжних з нею вершин. Наприклад, для організації графу D список суміжності має бути таким, як зображено на рис.2.

1 2

2 3 4

3

4 1 3

Рис.2. Список суміжності графу

Граф, в якому кожному ребру (i,j) відповідає число wij називається зваженим, а число wij називається вагою ребра (i,j). Зважений граф можна зобразити матрицею вагів, що утворюється з матриці суміжності, коли її одиничні елементи замінити на відповідні ваги. Вага неіснуючого ребра вважається рівною нескінченості або нулю.

Найкоротші шляхи у графі

Шляхом, що з’єднує вершини a і b графу G, називається послідовність вигляду вершина 1, ребро 1, вершина 2, …, ребро N-1, вершина N, де вершина 1 = a, вершина N = b, а i-те ребро інцедентне з i-ю та (i+1)-ю вершинами.

Для будь-яких двох вершин vi та vj графу G може існувати декілька шляхів, що з’єднують їх. Для визначення у зваженому графі шляху, який має мінімальну вагу серед інших шляхів, що

81

починаються в заданій вершині start, а завершується у вершині finish розглядається наступна задача. Нехай зважений орієнтований граф G=(V,E) заданий матрицею суміжності А і ваги всіх його дуг невід’ємні. Якщо дуга від вершини vi до вершини vj відсутня, то Aij=∞.

Одним із найвідомішим розв’язань цієї задачі є алгоритм Дейкстри. На кожній ітерації цього алгоритму множина Т вершин, найкоротші шляхи до яких від вершини start уже визначено, збільшується на один елемент. Крім множити Т розглядається масив Path. Нехай Pi

– множина всіх шляхів з вершини start, останні дуги яких починаються у вершинах множини Т, а

шляху від вершини start до вершини m, розглядається довільний шлях q, що розпочинається у вершині start, а завершується у згаданій вершини m. Нехай k – найперша вершина на шляху,

його виконання потребує O(n) кроків: O(n) кроків для розрахунку довжин шляхів до кожної вершини і O(n) кроків для пошуку найкоротшого шляху. Отже, складність алгоритму становить

O(n2).

Реалізація алгоритму Дейкстри мовою Pascal:

program yrok11;

//Пошук найкоротших шляхів за алгоритмом Дейкстри {$APPTYPE CONSOLE}

uses SysUtils;

const MaxSize=150; //найбільша кілкість вершин графу infinity=10000; //позначення нескінченості

type

VertexSet = set of 1..Maxsize;

var //довжини шляхів або ваги ребер графу weigth: array[1..Maxsize, 1..Maxsize] of integer;

T: VertexSet; //множина вершин, до яких визначено найкоротші шляхи Path, //масив довжин найкоротших шляхів до кожної вершини графу Vertex: array[1..Maxsize] of integer; //масив вершин найкоротшого шляху n: integer; //кілкість вершин графу

start, finish: integer; //початкова та кінцева вершини графу f: text; //файл вхідних даних, що містить кількість вершин

//та матрицю суміжності

82

//формування матриці суміжності procedure ReadData;

var i,j: integer; begin

assign(f,'Deyksra.txt'); reset (f);

readln(f,n); for i:=1 to n do

for j:=1 to n do read(f,weigth[i,j]);

close(f);

end;

//виведення матриці суміжності procedure OutPutData;

var i,j: integer; begin

writeln('Adjacency matrix'); for i:=1 to n do

begin

for j:=1 to n do

if weigth[i,j]=infinity then write('-':10) else write(weigth[i,j]:10);

writeln;

end;

end;

//алгоритм Дейкстри procedure FindMinPath;

var min: integer; //довжина найкоротшого шляху i,j: integer;

begin

// підготовка до пошуку найкоротшого шляху for i:=1 to n do

Path[i]:= infinity; //найкоротший шялх не визначено j:=start; // перша вершина найкоротшого шляху

T:=[j]; // множина Т містить початкову вершину start Path[j]:=0; // шлях зі start у start має довжину 0

//пошук найкоротшого шляху while not (finish in T) do

begin

for i:=1 to n do //перевіряти всі вершини begin

//якщо поточна вершина не належить множині Т, //знайти найменшу суму шляхів до неї

if not (i in T) and (Path[i]>Path[j]+weigth[j,i]) then begin

//запам"ятати вагу найкоротшлго шляху до поточної вершини //та номер попередної вершини

83

Path[i]:=Path[j]+weigth[j,i];

Vertex[i]:=j;

end;

end;

//пошук нового елемента множини Т min:=infinity;

j:=0;

for i:=1 to n do

//якщо вершина не належить до множини Т, //а шлях до неї менший за мінімальний

if not (i in T) and (min>Path[i]) then begin

min:=Path[i]; //вважати шлях до поточної вершини найкоротшим, j:=i; //а її саму - кандидатом на включення до множини Т

end;

//якщо немає шляху від початкоіої до поточної вершини if min>=infinity

then begin

writeln('There is no way from vertex', start,'to vertex', finish); readln;

halt(0); //завершити роботу програми після відповідного повідомлення end

else T:=T+[j];

end; // кінець пошуку найкоротшого шляху end;

//виведення найкоротшого шляху procedure WriteMinPath;

var i: integer;

while i<>start do //поки не досягнуто номера початкової вершини

writeln('Length=',Path[finish]); //вивести довжину найкоротшого шляху end;

//основний блок програми begin

ReadData; // OutPutData; // repeat //

writeln('Enter start vertex <=',n); readln(start);

until start<=n;

84

repeat //

writeln('Enter finish vertex <=',n); readln(finish);

until start<=n; FindMinPath; // WriteMinPath; // readln;

end.

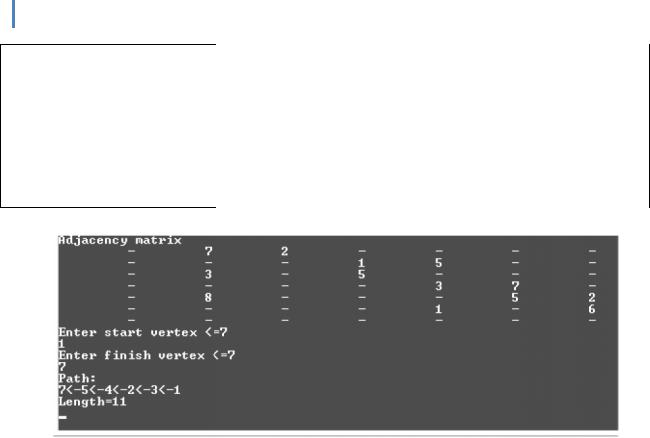
Результат роботи програ ми, що реалізує алгоритм Дейкстри, предс тавлений на рис.3.

Рис.3.Результат роботи програми Yrok11

85

Тема 25. АЛГОРИТМ ДЕ ЙКСТРИ ВИЗНАЧЕННЯ НАЙКОРОТШОГО ШЛЯХУ МІЖ ВЕРШИНАМИ ГРАФУ

Алгоритм Дейкстри — алгоритм на графах, відкритий Дейкстрою - знаходить найкоротший шлях від однієї вершини графа до всіх інших вершин. Класичний алгоритм Дейкстри працює тільки для графів без дуг

від'ємної довжини.

Формулювання задачі

Варіант 1. Дана мережа автомобільних доріг, що з'єднують міста Львівської області. Знайти найкоротшу відстань в ід Львова до кожного міста області, якщо рухатись можна тільки по дорогах.

Варіант 2. Дана карта велосипедних доріжок Латвії та Білорусі. Знайти мінімальну

відстань, яку треба проїхати, щооб дістатися від Риги до Бобруйська.

Варіант 3. Є план міста з нанесеними на нього місцями розміщен ня пожежних частин.

Знайти найближчу до кожного дому пожежну станцію.

Абстракція

Дано неорієнтований зв' язний граф G(V, U). Знайти відстань від ве ршини a до всіх інших

вершин V.

Інтуїтивне пояснення

Зберігатимемо поточну мінімальну відстань до всіх вершин V (від даної вершини a) і на кожному кроці алгоритму намаг атимемося зменшити цю відстань. Спочатку встановимо відстані до всіх вершин рівними нескінче ності, а до вершини а — нулю.

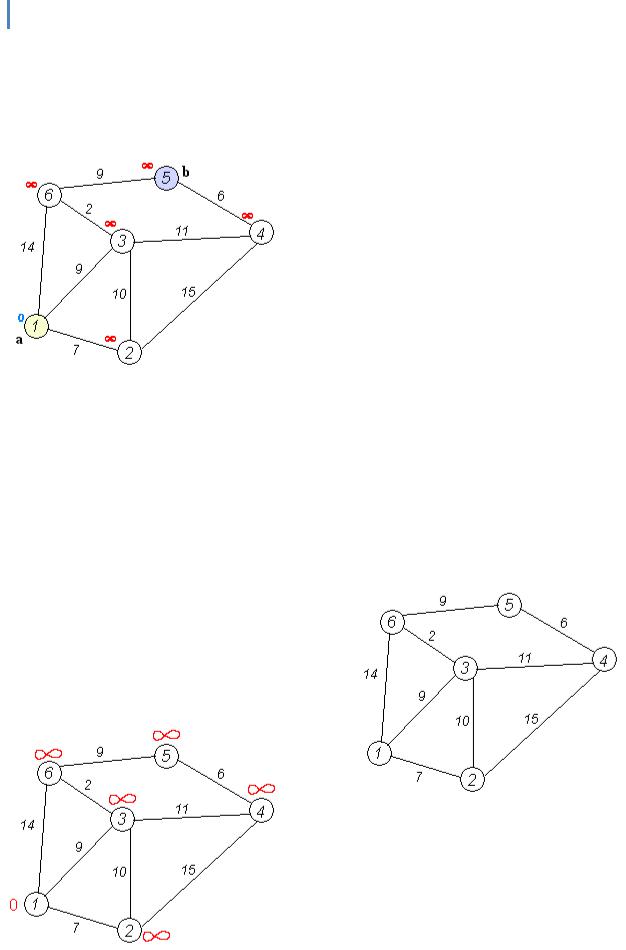
Розглянемо виконання алгоритму на прикладі. Хай потрібно знайти відстані від 1-ої вершини до всіх інших. Кружечками позначені вершини, лініями — шляхи між ними («дуги»). Над дугами позначена їх « ціна» — довжина шляху. Надписом над круж ечком позначена поточна найкоротша відстань д о вершини.

Крок 1

Ініціалізація. Відстань до всіх вершин графа V = 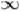. Відстань до а = 0. Ж одна вершина графа ще не опрацьована.

86

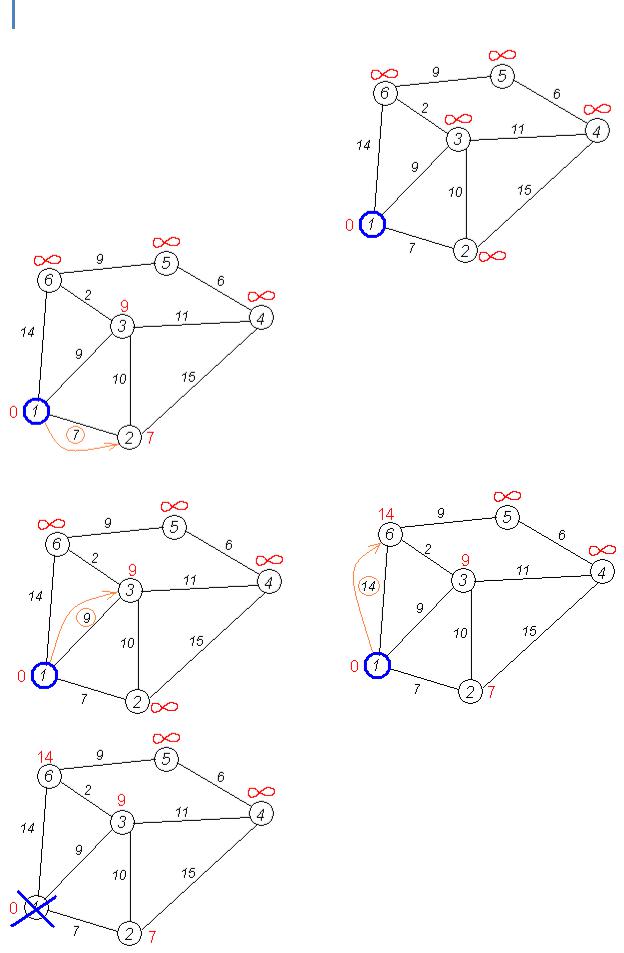
Крок 2

Знаходимо таку вершину (із ще не оброблених), поточна найкоротша відстань до

якої мінімальна. В нашому випадку це вершина 1. Обходимо всіх її сусідів і, якщо шлях в сусідню вершину через 1 менший за поточний мінімальний шлях в цю сусідню вершину, то запам'ятовуємо цей новий, коротший шлях як поточний найкоротший шлях до сусіда.

Крок 3

Перший по порядку сусід 1-ї вершини — 2-а вершина. Шлях до неї через 1-у вершину дорівнює найкоротшій відстані до 1-ї вершини + довжина дуги між 1-ю та 2-ю вершиною, тобто 0 + 7 = 7. Це менше поточного найкоротшого шляху до 2-ї вершини, тому найкоротший шлях до 2-ї вершини дорівнює 7.

Кроки 4, 5

Аналогічну операцію проробляєм з двома іншими сусідами 1-ї вершини — 3-ю та 6-ю.

Крок 6

Всі сусіди вершини 1 перевірені. Поточна мінімальна відстань до вершини 1 вважається остаточною і обговоренню не підлягає (те, що це дійсно так, вперше довів Дейкстра). Тому викреслимо її з графа, щоб відмітити цей факт.

87

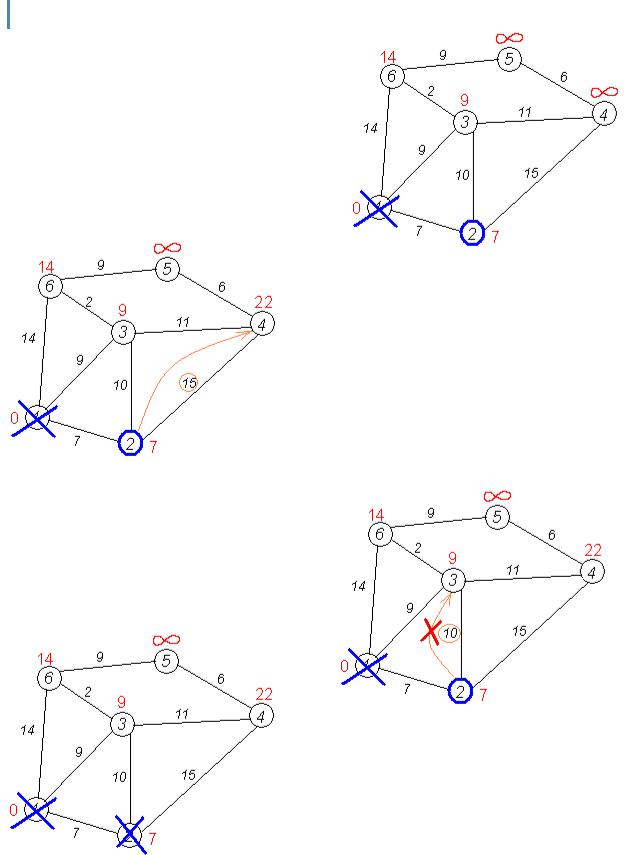
Крок 7

Практично відбувається повернення до кроку 2. Знову знаходимо «найближчу» необроблену (невикреслену) вершину. Це вершина 2 з поточною найкоротшою відстанню до неї = 7. І знову намагаємося зменшити відстань до всіх сусідів 2-ої вершини, намагаючись пройти в них через 2-у. Сусідами 2- ої вершини є 1, 3, 4.

Крок 8

Перший (по порядку) сусід вершини №2— 1- а вершина. Але вона вже оброблена (або викреслена — див. крок 6). Тому з 1-ою вершиною

нічого не робимо.

Крок 8 (з іншими вхідними данними)

Інший сусід вершини 2 — вершина 4. Якщо йти в неї через 2-у, то шлях буде = найкоротша відстань до 2-ої + відстань між 2-ою і 4-ою вершинами = 7 + 15 = 22. Оскільки 22 < ∞,

встановлюємо відстань до вершини № 4 рівним 22.

Крок 9

Ще один сусід вершини 2 — вершина 3. Якщо йти в неї через 2-у, то шлях буде = 7 + 10 = 17. Але 17 більше за відстань, що вже запам'ятали раніше до вершини № 3 і дорівнює 9, тому поточну відстань до 3-ої вершини не міняємо.

Крок 10

Всі сусіди вершини 2 переглянуті, заморожуємо відстань до неї і викреслюємо її з графа.

88

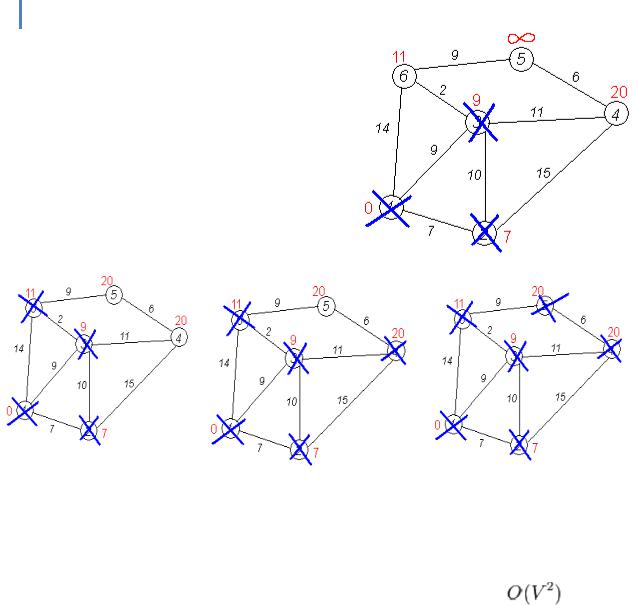
Кроки 11 — 15

По вже «відпрац ьованій» схемі повторюємо кроки 2 — 6. Теп ер «найближчою» виявляється вершина № 3. Після її «обробки» отримаємо такі результати:

Наступні кроки

Проробляємо те саме з вершинами, що залишилися (№ по порядку: 6, 4 і 5).

Завершення виконання алгоритму

Алгоритм закінчує роботу, коли викреслені всі вершини. Результат його роботи видно на останньому малюнку: найкорот ший шлях від 1-ої вершини до 2-ої складає 7, до 3-ої — 9, до 4-ої

— 20, до 5-ої — 20, до 6-ої — 11 умовних одиниць.

заповнюються великим позитивним числом (більшим максимального можливого шляху в графі), а масив позначок заповнюється нулями. Потім відстань для початкової вершини вважається рівною нулю і запускається осно вний цикл.

На кожному кроці циклу ми шукаємо вершину з мінімальною відстанню і прапором рівним нулю. Потім ми встановлюємо в ній позначку 1 і перевіряємо всі сусідні з нею вершини. Якщо в ній відстань більша, ніж сума відстані до поточної вершини і довжини ребра, то зменшуємо його. Цикл завершується коли позначки всіх вершин стають рівними 1.

Алгоритм Дейкстри в математичних термінах

присвоюється значення Di, U присвоюється U {i} і виконується перехід до кроку 2.

89

Текст програми

#Include <iostream.h>

#Include <string.h>

#Include <stdio.h>

#Include <stdlib.h>

#Include <conio.h>

#Define word unsigned int

int i, j, n, p, xn, xk; int flag [11]; word c [11] [11], l [11]; char s [80], path [80] [11]; int min (int n)

{

int i, result;

for (i = 0; i <n; i + +) if (! (flag [i])) result = i; for (i = 0; i <n; i + +)

if ((l [result]> l [i ])&&(! flag [i])) result = i; return result;

}

word minim (word x, word y)

{

if (x <y) return x; return y;

}

void main ()

{

cout <<"Vvedite kolichestvo tochek:"; cin>> n;

for (i = 0; i <n; i + +)

for (j = 0; j <n; j + +) c [i] [j] = 0; for (i = 0; i <n; i + +)

for (j = i +1; j <n; j + +)

{

cout <<"Vvedite rasstoyanie ot x" <<i +1 <<"do x" <<j +1 <<":"; cin>> c [i] [j];

}

cout <<"";

for (i = 0; i <n; i + +) cout <<"X" <<i +1; cout <<endl <<endl;

for (i = 0; i <n; i + +)

{

printf ("X% d", i +1); for (j = 0; j <n; j + +) { printf ("% 6d", c [i] [j]); c [j] [i] = c [i] [j];

}

printf ("\ n \ n");

}

for (i = 0; i <n; i + +) for (j = 0; j <n; j + +)

if (c [i] [j] == 0) c [i] [j] = 65535; / / нескінченність cout <<"Vvedite nachalnuy tochku:";

cin>> xn;

90

91

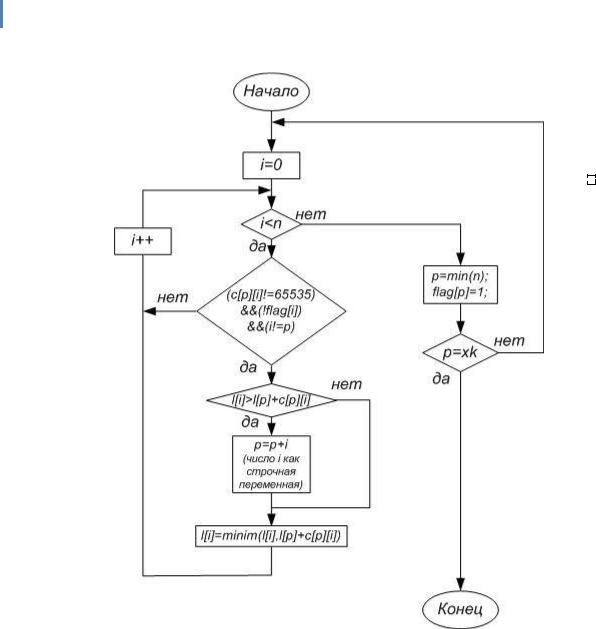
Схема програмної реалізації алгоритму Дейкстри

92