Тема 19: ДВОНАПРЯМЛЕНІ ЛІНІЙНІ СПИСКИ

У двонапрямлених списках і в розглянутих раніше однонапрямлених елементи утворюють лінійну структуру даних з послідовним доступом, але на відміну від них, рух по списку можливий у двох напрямках, тому кожен елемент міститиме, окрім інформаційного поля, два вказівні поля: на наступний і попередній елементи. Список матиме два фіксованих вказівники: на перший – first; на останній – last.

Оскільки рух по списку можливий у двох напрямках, то переміщення від first до last здійснюється через вказівник next; від last до first через вказівник prev, тому формування списку за правилом стеку від first до last – це та ж сама черга від last до first і навпаки.Як і в однонапрямлених

списках над двонапрямленими виконують ті ж самі операції.

Оголошення структури списку може мати вигляд:

TYPE list2=^el_list2; el_list2=record inf:integer; next,prev:list2 END;

Формування списку

writeln('введіть кількість елементів у списку'); readln(n);

first:=nil;

last:=nil;

for i:=1 to n do begin

writeln('введіть елемент'); readln(a);

new(p);

p^.inf:=a;

if last=nil then last:=p; p^.next:=first; first^.prev:=p;

first:=p

end;

2. Перегляд. Здійснюється аналогічно, тільки може здійснюватися в обоз напрямках.

PROCEDURE RESIV; BEGIN

p:=first;

while p^.next<>nil do begin

write(p^.inf,' '); p:=p^.next end; writeln(p^.inf,' ')

60

END;

3. Пошук

p:=first;

writeln('введіть шуканий елемент'); readln(a);

i:=0;

while (p<>nil) do begin

inc(k);

if p^.inf=a then begin

i:=i+1; writeln('під № ',k) end;

p:=p^.next

end;

if i=0 then writeln ('немає') else writeln ('кількість ',i)

4.Вставка перед на відмінну від однонапрямленого списку аналогічна вставці після з точністю переміни вказівників prev і next.

write('введіть елемент, після якого потрібно вставити новий'); readln(n);

write('введіть новий елемент'); readln(a);

p:=first;

while p<>nil do begin

if p^.inf=n then begin new(q);

q^.next:=p^.next;

p^.next:=q;

q^.prev:=p

end;

q^.inf:=a;

p:=p^.next

end;

5. Вилучення. Як і в попередніх випадках видалення елементу не потребує складного пошуку із порівнянням через один елемент, як у однонапрямлених списках.

write('введіть елемент, який потрібно вилучити'); readln(a);

p:=first;

while p<>nil do begin

61

if p^.inf=a then begin

if p=first then begin first:=p^.next; p^.prev:=nil end

else begin

if p^.next<>nil then begin p^.next^.prev:=p^.prev;

p^.prev^.next:=p^.next^.next end

else begin

p^.prev^.next:=nil

end;

end; end else

p^.prev^.next:=p;

p:=p^.next

end;

62

Тема 20. ДЕРЕВА. СТВОРЕННЯ ТА ОБХІД БІНАРНОГО ДЕРЕВА

Списки, стеки та черги належать до лінійних динамічних структур даних. Визначальною характеристикою лінійних структур є те, що зв'язок між їхніми компонентами описується в термінах «попередній-наступний», тобто для кожного компонента лінійної структури визначено не більше одного попереднього та не більше одного наступного компонента. Деревоподібна структура даних, або дерево, є нелінійною структурою, тобто зображує ієрархічні зв’язки типу «предок-нащадок»: компонент-предок може мати багато нащадків, хоча для кожного компонента нащадка визначено не більше одного предка.

Основні поняття

Згідно з рекурсивним означенням, дерево з базовим типом Т – це або порожня структура, або вузол типу Т, з яким зв’язана скінчена кількість дерев із базовим типом Т, які називають піддеревами. Із означення випливає, що піддерева (гілки) будь-якого вузла не перетинаються, тобто не мають спільних вузлів. Ця властивість розглядуваних структур і споріднює їх із справжніми деревами, адже гілки дерева «зростатися» не можуть.

Вузол дерева, який не має предків, називається коренем. Серед будь-якої пари безпосередньо зв’язаних вузлів можна виділити предка та нащадка. Вважається, що корінь дерева розташований на першому рівні. Кожний вузол-нащадок рівня k має предка на рівні k-1. Максимальний рівень дерева називається його глибиною або висотою.

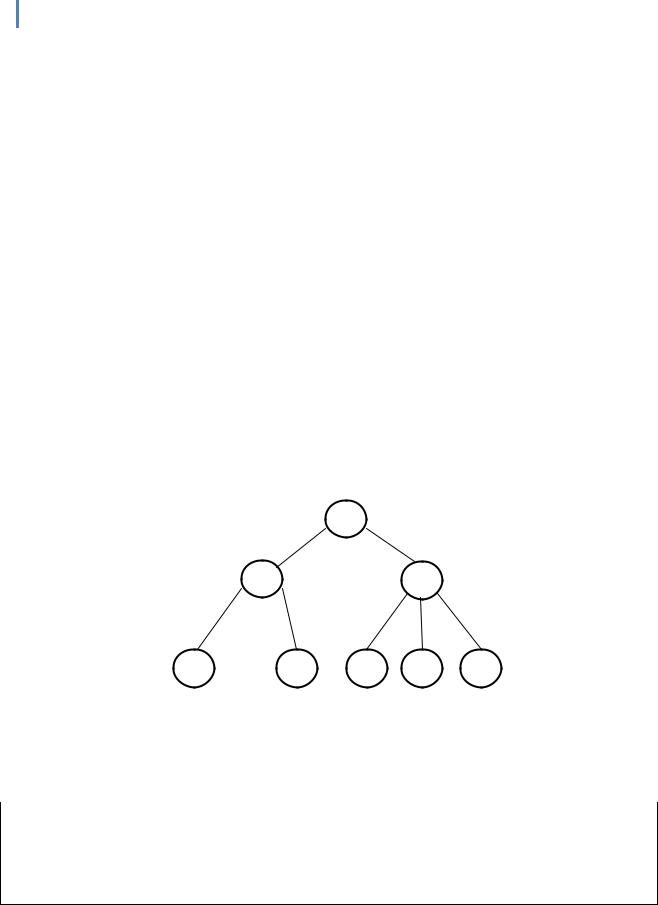
На рис.1 зображене дерево, глибина якого дорівнює 3. Вузол дерева, який не має нащадків, називається листком. Кількість безпосередніх нащадків вузла називається його степенем. Максимальний степінь вузла у певному дереві називається степенем дерева.

А

B C

D E F G H

Рис.1. Дерево Далі розглядатимуться лише бінарні дерева, тобто дерева, степінь яких не перевищує

двох. Отже, будь-який вузол бінарного дерева може бути зв’язаним не більше ніж з двома піддеревами, що називаються лівим і правим піддеревами вузла. Оголошення типу вузла бінарного дерева на мові Pascal має наступний вигляд:

Для листків покажчики left та right мають значення nil. Приклад бінарного дерева як структури даних наведено на рис.2.

63

Рис.2 Дерево як структура даних

Алгоритми роботи з бінарними деревами

Найпоширенішими операціями під час роботи з деревами є:

∙створення дерева;

∙включення вузла в дерево;

∙видалення вузла з дерева;

∙обхід дерева;

∙пошук у дереві.

Створення бінарного дерева

Найпростіший спосіб побудови бінарного дерева полягає у створенні дерева симетричної структури із наперед відомою кількістю вузлів. Усі вузли-нащадки, що створюються, рівномірно розподіляються зліва та справа від кожного вузла-предка. При цьому досягається мінімально можлива глибина для заданої кількості вузлів дерева. Правило рівномірного розподілу n вузлів можна визначити рекурсивно:

∙перший вузол вважати коренем дерева;

∙створити ліве дерево з кількістю вузлів nleft := n div 2;

∙створити праве дерево з кількістю вузлів nleft := n – nleft -1;

Програма Yrok9_1 реалізує розглянутий алгоритм. Оскільки структура дерева визначена рекурсивно, то для його створення та відображення використовуються рекурсивні підпрограми.

Функція створення дерева Tree отримує один цілочисловий параметр AmountNode, що визначає кількість вузлів дерева та повертає покажчик на його корінь. Якщо кількість вузлів дорівнює нулю, дерево порожне, тобто виконано умову завершення рекурсії і функція має повернути значення nil. Якщо кількість вузлів відмінна від нуля, необхідно виділити пам'ять для кореня дерева, за наведеними формулами обчислити кількість вузлів у лівому і правому під деревах і двічі рекурсивно викликати функцію Tree для створення піддерев.Для посилання на корінь дерева використовується локальний покажчик newnode. Значення покажчиків на корені піддерев, що їх повертатиме функція Tree в результаті рекурсивних викликів, слід присвоїти полям left та right змінної newnode^.

Дерево відображатиме рекурсивна процедура printtree. Піддерево півня L виводитиметься так: спочатку буде відображене ліве піддерево, потім корінь піддерева рівня L, перед яким буде виведено L пробілів, далі – праве піддерево.

64

program Yrok9_1;

{Створення бінарного дерева} {$APPTYPE CONSOLE}

var n: integer; {кількість вузлів дерева} root: ptr; {покажчик на корінь дерева}

{===створення бінарного дерева===} function Tree(AmountNode: integer): ptr; {AmountNode - кількість вузлів дерева} {ptr - покажчик на корінь дерева}

Rightnode:= AmountNode - Leftnode -1; {кількість вузлів у правому піддереві} write('Enter node data: '); readln(str);{введення значень інформаційних полів} New(newnode); {виділення пам"яті для нового вузла}

left :=Tree(Leftnode); {створити ліве піддерево} right:=Tree(Rightnode); {створити ліве піддерево} end;

Tree:=newnode; {значення, що повертається} end;

end;

{===відображення дерева===}

procedure PrintTree(RootTree: ptr; L: integer); {RootTree - покажчик на корінь дерева}

{L - номер рівня}

var i: integer; {параметр циклу} begin

65

for i:=1 to L do write(' '); writeln(data);

PrintTree(right,L+1); {вивести праве піддерево} end;

end;

{===головна програма====} begin

writeln('Create and display tree');

write('Enter number of tree ''s nodes '); readln(n); {ввести кількість вузлів дерева}

Результати виконання пр ограми та графічний вигляд створеного нею дерева наведені на рис.3,4. Дерева такого типу наз иваються синтаксичними деревами арифметичних виразів.

Рис.3.Результати роботи програми Yrok9_1. Створ ення та відображення бінарного дерева

*

+-

Рис.4. Бінарне дерево, створене програмою Yrok9_1

Обхід дерева

Алгоритм доступу до всі х вузлів дерева називається обходом дерев а. Трьома основними способами обходу дерева є:

∙зверху вниз;

∙зліва направо;

∙знизу вверх.

66

Якщо при обході дерева, що зображене на рис.4, виписувати значення його вузлів у тому порядку, в якому вони трапляються під час обходу, то можна отримати наступні послідовності символів:

У результатів обходу синтаксичного дерева зверху вниз утворюється префіксна форма виразу, при обході знизу вверх – постфіксна, а при обході зліва направо – інфіксна. Будь-який спосіб обходу дерева можна реалізувати рекурсивною процедурою. Такі процедури наведені в наступному прикладі, який реалізує три рекурсивні процедури обходу бінарного дерева. До цих процедур передається параметр-значення, що є покажчиком на корінь дерева. Тіло всіх трьох процедур містить однаковий набір операторів Першою виконується перевірка того, чи не є дерево порожнім. Якщо дерево порожнє, здійснюється рекурсивне повернення, а в іншому разі виводиться значення вузла і рекурсивно викликаються процедури обходу для лівого і правого піддерев. Порядок цих трьох операторів і визначає форму виразу, що буде створений у результаті обходу. А саме, якщо виведення значення вузла виконуватиметься першим, то буде отримано префіксну форму виразу, якщо другим – інфіксну, а якщо третім – постфіксну форму. Код процедур обходу дерева наступний.

{===обхід дерева зверху вниз===} procedure Prefixorder(RootTree: ptr); begin

if RootTree<>nil then begin write(RootTree^.data,' ');

Prefixorder(RootTree^.left); Prefixorder(RootTree^.right); end;

end;

{===обхід дерева знизу вверх===} procedure Postfixorder(RootTree: ptr); begin

if RootTree<>nil then begin

Postfixorder(RootTree^.left); Postfixorder(RootTree^.right); write(RootTree^.data,' ');

end;

end;

{===обхід дерева зліва направо===} procedure Intfixorder(RootTree: ptr); begin

if RootTree<>nil then begin

Intfixorder(RootTree^.left); write(RootTree^.data,' '); Intfixorder(RootTree^.right); end;

end;

67

В основній програмі об ходу дерева здійснюється виклик всіх трьох процедур після виклику функції створення дерева та його відображення:

{===головна програма обходу дерева===} begin

writeln('Create and display tree');

write('Enter number of tree ''s nodes '); readln(n); {ввести кількість вузлів дерева}

writeln;

writeln('Prefixorder traversal'); Prefixorder(root);

writeln;

writeln('Postfixorder traversal'); Postfixorder(root);

writeln;

writeln('Intfixorder traversa l'); Intfixorder(root);

writeln;

readln;

end.

Результат роботи програ ми обходу дерева наведений на рис.5

Рис.5.Результати роботи програми Yrok9_2.

68