
Лабораторная работа №1
Этапы системного анализа на примере задач линейного программирования (ЛП).
Цель: систематизировать знания про этапы моделирования, изучить математическую модель задач линейного программирования, рассмотреть графический метод решения задачи линейного программирования.
Порядок выполнения:
Совместно изучить теоретическую часть, разобрать приведенный пример.
Решить задачи в практической части и продемонстрировать преподавателю.
Оформить отчет и сдать преподавателю.
Теоретическая часть План
Этапы моделирования.
Линейное программирование (математическая модель).
Базовая задача для демонстрации.
Графический метод решения задач ЛП.
При решении большинства практических задач используется моделирование, которое включает в себя следующие этапы:
Формализации исходной проблемы.
Построение математической модели.
Решение модели.
Проверка адекватности модели.
Реализация решения.
Формализация проблемы требует исследования той предметной области, где возникла рассматриваемая проблема. Это начальный этап работы любой команды аналитиков. В результате такого исследования должны быть получены следующие три принципиальных элемента решаемой задачи:
описание возможных альтернативных решений,
определение целевой функции,
построение системы ограничений, накладываемых на возможные решения.
Построение математической модели означает перевод формализованной задачи, описание которой получено на предыдущем этапе, на чёткий язык математических отношений. Если модель является одной из стандартных математических моделей, таких как линейное программирование, то решение достигается путём использования соответствующих существующих алгоритмов. Иначе модель может быть упращена аналитиками до стандартной либо используют имитационное и эвристическое моделирование.
Решение модели наиболее из простых этапов так как используются известные алгоритмы. Важный аспект этого этапа – анализ чувствительности полученного решения. Это получение дополнительной информации о поведении «оптимального решения» при изменении некоторых параметров модели.
Проверка адекватности модели предполагает проверку правильности модели, т.е. соответствует ли поведение модели в определённых ситуациях поведению исходной модели. Модель считается адакватной, если при определённых начальных условиях ее поведение совпадает с поведением исходной системы при тех же условиях.
Реализация решения подразумевает перевод результатов решения модели в рекомендации, представленные в форме, понятной для лиц, принимающих решения, т.е. заказчиков решения исходной проблемы.
Линейное программирование (ЛП) – это метод математического моделирования, разработанный для оптимизации использования ограниченных ресурсов. Широкое использование ЛП подкрепляется и высокоэффективными компьютерными алгоритмами, реализующими данный метод. На алгоритмах ЛП базируются алгоритмы других более сложных типов моделей.
Задача линейного программирования ставится следующим образом. Требуется отыскать условный экстремум (максимум или минимум) линейной целевой функции n переменных.
![]() (1.1)
(1.1)
При
этом на переменные (х1,
х2,
…, xn)
наложены линейные
ограничения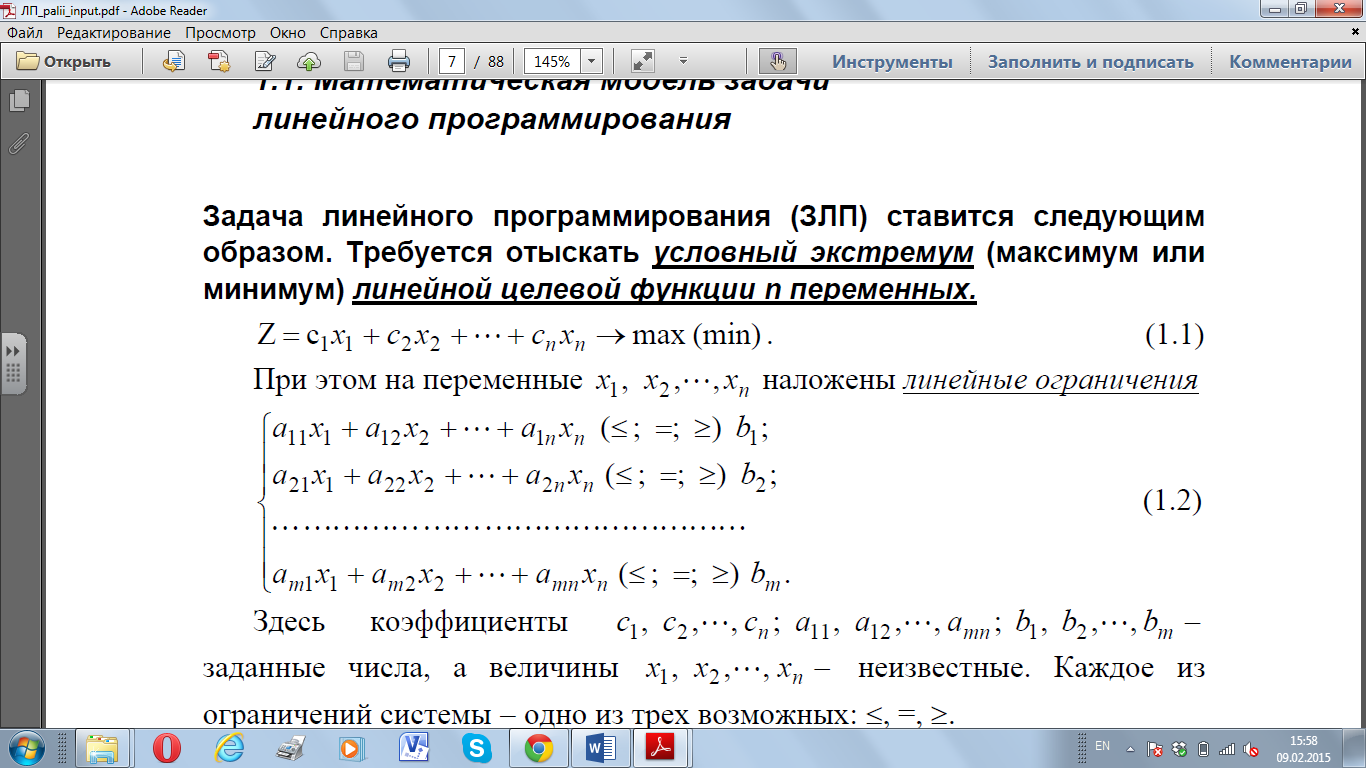
(1.2)
Коэффициенты с1, с2, …, сn; а11, а12,…, аmn; b1, b2, …, bn – заданные числа, а величины х1, х2, …, xn – неизвестные. Каждое из ограничений системы – одно из трёх возможных: ≤, =, ≥.
Совокупность целевой функции (1.1) и системы ограничений (1.2) называется математической моделью задач линейного программирования.
Свойства линейности функции предполагают следующее:
Значения левых частей неравенств ограничений и значение целевой функции прямо пропорциональны значениям переменных.
Аддитивность переменных – общий вклад всех переменных в значения целевой функции и левых частей неравенств ограничений является прямой суммой вкладов каждой отдельной переменной.
Любой набор чисел (х1, х2, …, xn), удовлетворяющий системе ограничений (1.2) называется допустимым решением задачи ЛП.
Допустимое решение, на котором достигается требуемый экстремум целевой функции (1.1) назывется оптимальным решением данной задачи ЛП.
Задача (модель) линейного программирования включает три основных элемента.
Переменные, которые следует определить.
Целевая функция, подлежащая оптимизации.
Ограничения, которым должны удовлетворять переменные.
Базовая задача для демонстрации элементов модели линейного программирования (результат этапа формализации исходной проблемы).
Компания "Весёлые краски" производит краску для внутренних и наружных работ из сырья двух типов: Ml и М2. Следующая таблица представляет основные данные для задачи:
|
|
Расход сырья на тонну краски |
Максимально возможный ежедневный расход сырья | |
|
|
Для наружных работ |
Для внутренних работ |
|
|
Сырье М1 |
6 |
4 |
24 |
|
Сырье М2 |
1 |
2 |
6 |
|
Доход, тис. ден. ед. на тонну |
5 |
4 |
- |
Отдел маркетинга компании ограничил ежедневное производство краски для внутренних работ до 2 т (из-за отсутствия надлежащего спроса), а также поставил условие, чтобы ежедневное производство краски для внутренних работ не превышало более чем на тонну аналогичный показатель производства краски для наружных работ. Компания хочет определить оптимальное (наилучшее) соотношение между видами выпускаемой продукции для максимизации общего ежедневного дохода.
Этап построения математической модели.
