4. Координати вектора

Нехай (,,) деякий базис простору,– довільний вектор цього простору. За теоремою про розклад вектора за трьома некомпланарними векторами існують єдині числа,,такі, що

=++.

Коефіцієнти ,,розкладу вектора за базисними векторами називаютьсякоординатами вектора в даному базисі. При цьому число називається першою координатою, число– другою, а число– третьою.

Якщо вектор в даному базисі має координати,,, то скорочено це записують так:(,,) або.

Встановимо геометричний зміст координат вектора в даному базисі. Для цього відкладемо вектори ,,івід деякої точкиО простору (мал. 16): =,=,=,=.

Побудуємо паралелепіпед, ребра якого напрямлені вздовж прямих ,,, а діагоналлю є відрізокOA. Тоді =++, де=,= =,=.

Тому =;

> 0, якщоі< 0, якщо;

=;

> 0, якщоі< 0, якщо.

Аналогічно, =;

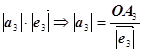> 0, якщоі< 0,.

Отже, координата з точністю до знака дорівнює довжині відрізкавиміряному в одиницях довжини. Знак же координатизалежить від напрямку векторіві:> 0, якщоі< 0, якщо. Аналогічно зміст двох інших координаті.

Базисні вектори в самому базисі мають координати (1; 0; 0),(0; 1; 0),(0; 0; 1).

Аналогічно визначаються координати вектора в просторі . Базис цього підпростору складається з двох не колінеарних векторів. Нехай система векторів,є базисом підпростору. Тоді за теоремою про розклад вектора за двома не колінеарними векторами для будь-якого вектораіз підпросторуіснують єдині числа,такі, що=+. Коефіцієнти,цього розкладу називаються координатами векторав базисі (,). Числоназивається першою координатою, а число– другою.

Аналогічним є і геометричний зміст координат вектора в підпросторі (мал. 17):

=+=+.

=,

> 0, якщоі< 0, якщо;

=;

> 0, якщоі< 0, якщо.

Базисні вектори мають координати: (1; 0),(0; 1). Координати вектора в даному базисі повністю задають вектор.

Розглянемо властивості координат векторів.

Теорема (2-га ознака рівності векторів): для того, щоб два вектори були рівними, необхідно і достатньо, щоб були рівними їх відповідні координати.

Твердження цієї теореми очевидне, воно випливає з єдиності розкладу вектора за трьома не компланарними векторами.

Теорема:справедливі такі твердження:

1)                 координати суми двох векторів дорівнюють сумі відповідних координат цих векторів;

2)                 координати різниці двох векторів дорівнюють різниці відповідних координат цих векторів;

3)                 координати добутку вектора на число дорівнюють добутку відповідних координат цього вектора на дане число.

Доведення: доведемо наприклад перше твердження. Нехай у деякому базисі (,,),(,,),(,,). Тоді за означенням координат вектора

=++,=++.

Отже, +=+++++= (+)+ (+)+ (+).

Звідси випливає, що координати вектора +відповідно дорівнюють+ +,+,+, що й треба було довести.

Аналогічно доводяться й інші властивості.

Теорема (2-га ознака колінеарності двох векторів): для того, щоб два вектори (,,),(,,) задані в деякому базисі (,,), були колінеарними, необхідно і достатньо, щоб їх координати були пропорційними.

Доведення:якщо=, то твердження очевидне. Припустимо, що.

1. Необхідність.Нехай||. Тоді існує таке число λ, що= λ, звідки випиває, що= λ,= λ,= λ;

= λ.

Отже, якщо вектори колінеарні, то їх координати пропорційні.

2. Достатність.Нехай= λ, тоді= λ,= λ,= λ. Помноживши ці рівності на вектори,,відповідно, дістанемо= λ,= λ,= λ. Додавши ці рівності дістанемо++= λ+ λ+ λабо++= λ(++), тобто= λ||. Теорему доведено.