няющихся сеток. Интересно отметить, что на практике в качестве сетки с самыми крупными ячейками используется даже сетка 3×3. И ее использование заметно повышает скорость сходимости итерационного процесса даже на поздних его стадиях, когда приближенное решение почти установилось к точному.

3.3.8.Организация метода Федоренко

На исходной сетке NS =1 делаем несколько итераций (будем делать

уравнения (17) H1 , расписанная на сетку NS = 2 .

Процесс укрупнения сетки продолжается до сетки, в которой расчетная область хотя бы по одному направлению покрывается двумя шагами сетки. После чего начинается обратный процесс: переход с укрупненных сеток на исходную. При этом, полученное на NS +1 решение интерполируется на сеткуNS и вносится поправка в решение, ранее полученное на

сеткеNS : ϕNS =ϕNS −ϕNSNS+1 . После чего делается еще несколько итераций на сетке NS и осуществляется переход на сетку NS −1.

3.3.9.Дискретная модель для оператора переноса

Напомним, что в рассматриваемом случае скорости постоянны во всей расчетной области.

81

При аппроксимации оператора переноса B в уравнении (4) считаем положительными обе компоненты скорости u ≥ 0 , v ≥ 0 . При иных знаках изменения очевидны.

Полагаем функцию ϕ постоянной в ячейке (n,m) в том смысле, что именно это значение переносится через правую и верхнюю границы ячейки, то есть

3.3.10.Метод решения дискретного уравнения переноса

Обращение начинаем с левого нижнего угла сетки, так как полагаем u > 0 , v > 0 . Если знаки u и v другие, то начинаем с других углов.

При нахождении ϕnm уже известны (вычислены на предыдущих ша-

Для контроля за точностью решения будем вычислять норму невязки уравнения (3). Итерационный процесс прекращается, когда норма невязки уменьшилась в требуемое количество раз, например, в 1000 или 10000.

82

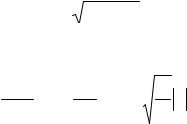
3.3.11. Сопоставление результатов численных расчетов с известными аналитическими моделями

Приведем результаты тестирования комплекса программ для численного решения двумерного уравнения диффузии с переносом и поглощением. Идеи и методы, положенные в основу алгоритма, описаны выше.

Вкачестве тестовой задачи была использована задача о диффузии аэрозоля, поставляемого точечным источником в безграничное пространство. Ветер, коэффициенты диффузии и поглощения считаются постоянными.

Вдвумерном случае уравнение имеет вид:

где ϕ – искомая концентрация аэрозоли; μ – коэффициент диффузии;

– двумерный оператор Лапласа; u – компонента скорости ветра в направлении x; v – компонента скорости ветра в направлении y; σ – коэффициент поглощения; δ(r − r0 ) – дельта-функция, задающая источник в точке с координатами r0 = (x0 , y0 ) , Q – интенсивность точечного источника.

Поместим начало координат в точку с координатами (x0 , y0 ) и раз-

вернем ось x по направлению ветра. Тогда уравнения можно переписать

83

β =σ +U 2 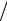(4μ) .

Функцию Макдональда вычисляли при помощи аппроксимирующих полиномов, обеспечивающих точное вычисление восьми значащих цифр.

Для изучения вопросов порядка аппроксимации точности и эффективности численного алгоритма, предназначенного для решения уравнения диффузии с переносом и поглощением в случае постоянных коэффициен-

Рис.8. Распределение концентрации аэрозоля вдоль осевой линии, ориентированной по ветру и проходящей через источник выбросов

84

тов переноса диффузии и поглощения, была проведена серия тестовых расчетов. Значения коэффициентов выбирали из интервала реально наблюдаемых коэффициентов диффузии, поглощения и скоростей ветра.

Расчеты проводили как на равномерной, так и на существенно неравномерной сетке (с отношением сторон разностной ячейки от 1 до 500). На равномерной сетке была показана квадратичная по шагу сетки сходимость численного решения к точному. (Исследование характера сходимости численного решения к точному – принятая норма в численном моделировании, позволяющая определить качество аппроксимации.) Неравномерная сетка позволяет экономить машинные ресурсы (память и время счета), если задача имеет существенно неоднородное по пространству решение. Так, в случае сильного ветра и слабой диффузии, когда отличные от нуля значения решения находятся вблизи полуоси начинающейся из источника и ориентированной по ветру, имеет смысл строить сетку с ячейками вытянутыми в этом направлении.

Результаты тестовых расчетов и их сопоставление с аналитическим решением (20) приведены на рис.8. Расчеты выполнены при следующих значениях безразмерных параметров Q =1; μ =1; U =10 ; σ =1.

На рис. 8 кривая, представленная тонкой сплошной линией соответствует точному решению задачи на оси x; кривая, представленная жирной линией – численный расчет в сетке 32×32 с равномерными шагами по x и y

– hx = hy = 0.25; пунктиром показан случай при hx = 0.0625 для −1 ≤ x ≤ 0

и hx = 0.25 при 0 < x < 6 , hy = 0.25. Решение, полученное в последнем случае, немного отличается от аналитического лишь в небольшой области с подветренной стороны и вблизи границы. В остальной области отличие в четвертом-пятом знаках. Отличие в самом источнике связано с особенностью аналитического решения в источнике. Поскольку источник представлен точкой не имеющей площади, то концентрация аэрозоля «внутри» та-

85

кого источника бесконечна. На практике эту особенность заменяют концентрацией примеси наблюдаемой, например, в устье заводской трубы.

Из рис.8 видно, что приближенное решение, полученное даже на грубой сетке, кривая 2, мало отличается от точного, (кривая 1), за исключением области с подветренной стороны. В этой области отличия приближенного решения от точного связаны с тем, что масштаб изменения решения

Рис. 9. Распределение концентрации аэрозоля выбрасываемого точечным источником, при скорости ветра 0.1 м/сек. Отличие линий уровня от концентрических кругов с подветренной стороны связано с граничным условием ϕ =0

86

меньше шага сетки. Хорошо видно, что с уменьшением шага сетки приближенное решение сходится к точному.

Задачу в безграничной области мы заменяем задачей в ограниченной области с заданной фоновой концентрацией на границе. На рис. 8 можно увидеть, какие возмущения вносит это граничное условие в случае, когда фоновая концентрация полагается равной нулю. Граница области распо-

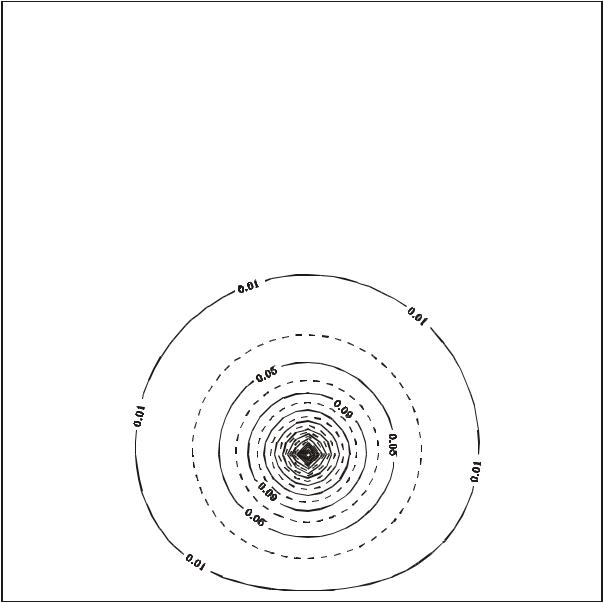
Рис. 10. Распределение концентрации аэрозоля выбрасываемого точечным источником, при скорости ветра 1 м/сек

87

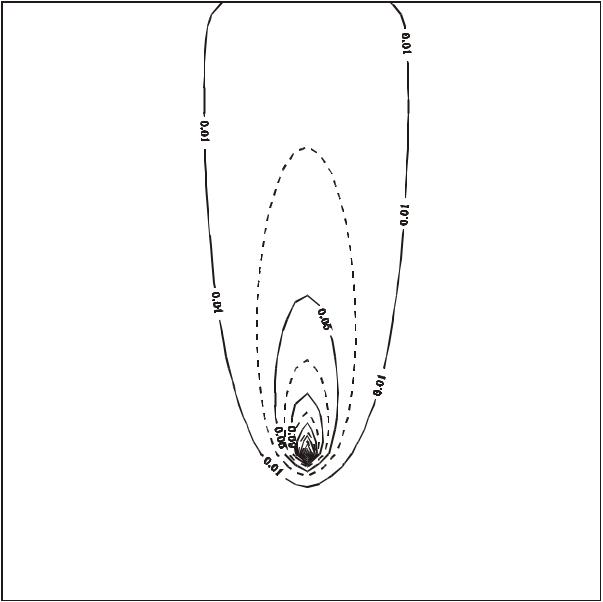
ложена на расстоянии x = 6. Видно, что отличие точного решения безграничной задачи от приближенного, соответствующего этому граничному условию, заметно лишь в 3-4 приграничных точках. Пример показывает, что сгущение сетки вблизи от источника в области высоких концентраций улучшает решение и внутри расчетной области и вблизи ее границы.

Анализ рисунка позволяет заключить, что ошибки в задании фоновой

Рис. 11. Распределение концентрации аэрозоля выбрасываемого точечным источником, при скорости ветра 10 м/сек

88

концентрации, которые неизбежны из-за недостатка информации, сказываются лишь в узкой приграничной полосе. При необходимости можно строить в приграничной зоне решение экстраполяцией решения из внутренней области. Тогда построенное решение будет соответствовать решению задачи в безграничной области.

Кроме описанных выше расчетов проводились и другие – для модели точечного источника с различными параметрами задачи. На рис 9-11 приведены результаты серии расчетов для точечного источника единичной

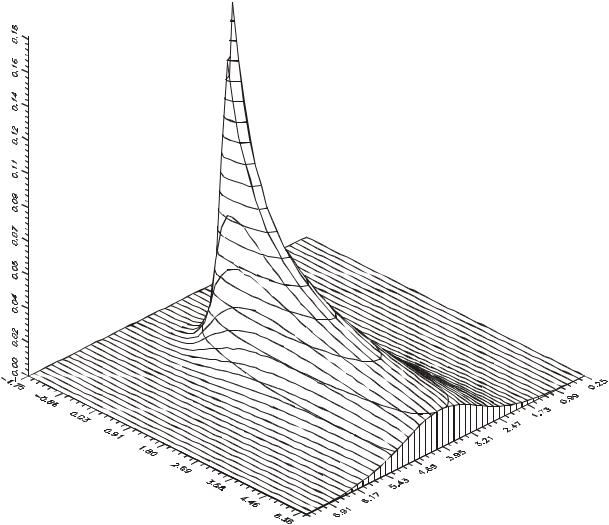
Рис.12. Трехмерная карта распределения концентрации (условия те же, что и на рис.11). На трехмерной поверхности более наглядно представлены различия концентрации в области

89

интенсивности при следующих параметрах: коэффициент диффузии

μ =10 м/с, коэффициент поглощения σ = 0 , скорость ветра вдоль оси y: v = 0, а вдоль оси x: u = 0.1; 1.0; 10 м/с. Сравнение с аналитическим реше-

нием показало, что решение, полученное численно во внутренних областях, отличается не более чем на 1% .

Из сравнения рис.10-12 видно, как с усилением ветра меняется картина распределения концентрации аэрозоля. Фактически уже при скольконибудь заметном ветре (1 м/с) аэрозоль сносится по ветру, и ее концентрация в области убывает.

Результаты сопоставления численных расчетов с аналитическими решениями (см. рис. 8) задачи о точечном источнике позволяют заключить, что предлагаемый алгоритм обеспечивает высокую точность решения в рамках данной модели.

90

3.3.12. Расчеты с распределенными источниками, моделирующими участки завода

Для того чтобы продемонстрировать работоспособность программ, предназначенных для расчетов пространственного распределения концентрации аэрозолей, выбрасываемых реальными объектами, приведем результаты некоторых расчетов с источниками, которые можно рассматривать как модели участка завода с источниками аэрозолей типа цех и труба. Расчеты выполнены по модели Паскуилла-Гиффорда. Модель включена в комплекс программ «Монитор», предназначенный для природоохранных служб промышленных предприятий.

Результаты численных расчетов представлены на рис. 13-15 в виде карт изолиний концентрации аэрозолей, выбрасываемых из труб точками и фонарей цехов. Расчеты тестовые отношения к реальному предприятию не имеют, уровень ПДК не задан. Результаты

На рис.13 показаны результаты расчетов для отдельного цеха. Цех моделируется с помощью точечных источников единичной интенсивности, расположенных в соседних узлах сетки.

Рис. 13-15 демонстрирует зависимость распределения концентрации от скорости ветра. Из сравнения рисунков видно, что по мере усиления ветра концентрация аэрозолей в расчетной зоне снижается, и распределение вытягивается по ветру. Особо обратим внимание на то, что даже при слабом ветре 5 м/с практически все выбросы сносятся по ветру и на рассматриваемых масштабах диффузия практически не играет роли.

На рис.15 показан случай, когда источниками выбросов являются цех и отдельно стоящая труба (такой же интенсивности выбросов, как и цех). Хорошо виден эффект суммирования концентрации аэрозоля.

91

Рис.13. Распределение концентрации аэрозоля выбрасываемого линейным источником (вытяжные фонари заводского цеха)

92

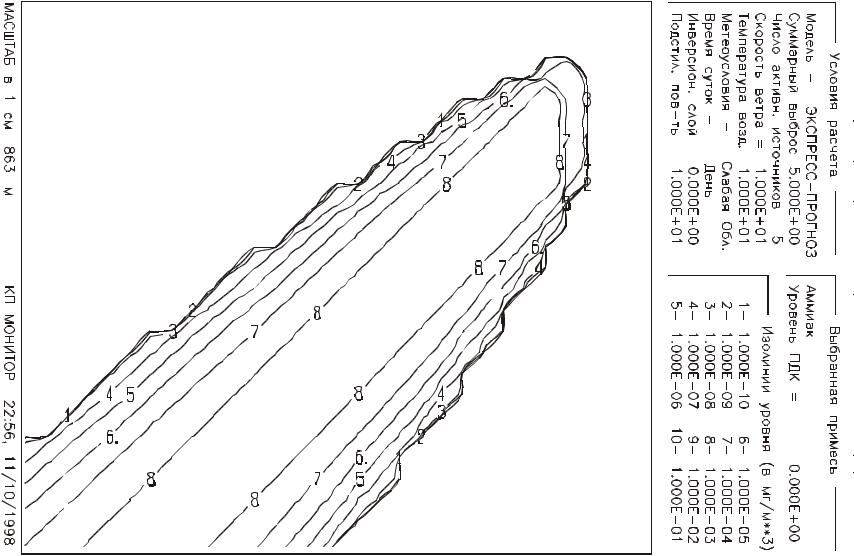
Рис.14. Распределение концентраций для тех же условий, что и на рис.13, но при скорости ветра 10м/сек

93

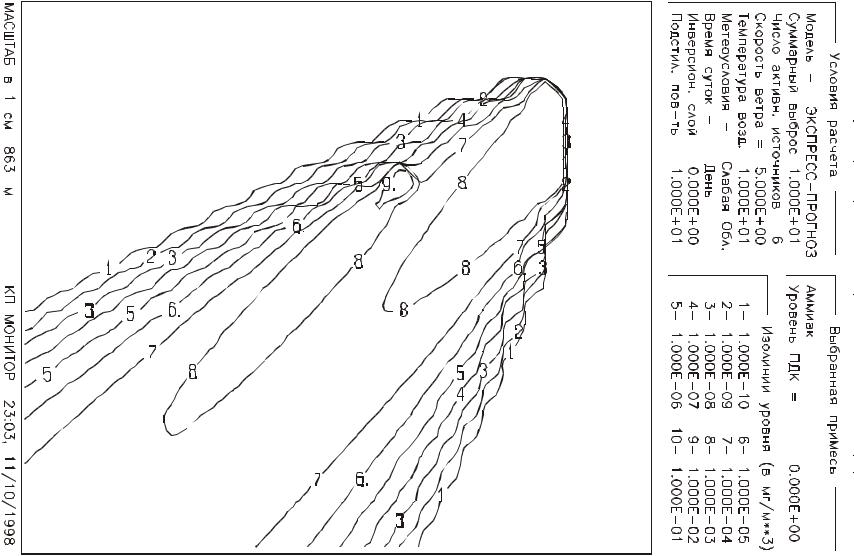
Рис.15. Распределение концентрации при скорости ветра 5м/сек и добавочном точечном источнике выбросов (заводская труба)

94

Представленные результаты достаточно наглядно демонстрируют работоспособность и возможности комплекса программ, предназначенного для расчетов установившегося распределения концентрации аэрозолей, которые выбрасывает в атмосферу множество источников, при произвольных направлении и силе ветра.

Список литературы

1.Ковеня В.М., Яненко Н.Н. Метод расщепления в задачах газовой динамики. Новосибирск: Наука, 1987 . 304 с.

2.Федоренко Р.П. Итерационные методы решения разностных эллипти-

ческих уравнений // УМН. 1973.Т.28. Вып.2(170). С.121-182.

3.Марчук Г.И. Математическое моделирование в проблеме окружающей среды. М.: Наука. Гл.ред. физ.-мат. лит., 1982. 320 с.

4.Янке Е., Эмдэ Ф., Леш Ф. Специальные функции.-М.: Наука, 1968. 344 с.

95