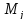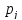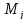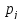- •Содержание Введение
- •1 Характеристика объекта проектирования
- •2 Статистическая обработка исходных данных
- •3 Проектирование сети передачи данных
- •3.1 Расчет числа билетно-кассовых терминалов
- •3.2 Расчет времени реакции системы
- •3.3 Построение сети передачи данных
- •4 Выбор программного обеспечения
- •5 Расчет затрат на создание системы
- •6 Разработка вопросов техники безопасности и охраны труда
- •Заключение
- •Список литературы
- •Приложение г Статистическая обработка данных Приложения в
- •Приложение д Расчет числа билетно-кассовых терминалов
- •Приложение е Расчет времени реакции системы
- •Приложение ж Топологическая схема сети передачи данных
Министерство образования Республики Беларусь
Учреждение образования
«Белорусский государственный университет транспорта»
Кафедра «Общетранспортные проблемы»
КУРСОВАЯ РАБОТА
по дисциплине
«Информационные системы на транспорте»
на тему
«Проектирование автоматизированной системы резервирования мест и продажи билетов на автовокзале»
|
Выполнил студент группы УА-51 Ханеев В.В. |
Проверил преподаватель Марковцев В.А. |
Гомель 2009
Содержание Введение
Развитие сложной вычислительной техники позволяет сегодня избавить человека от необходимости выполнения огромного количества как простых, так и очень сложных расчетов, что в свою очередь позволяет повысить точность и производительность труда. Однако применение изолированных вычислительных машин неэффективно, когда дело касается взаимосвязанных вычислений и производимых операций, которые выполняются на разных ЭВМ одновременно и требуется их сторонние контроль и координация.
С целью решения данного вопроса отдельные машины с помощью специального оборудования объединяют в сети. В зависимости от количества объединяемых ЭВМ, требуемой пропускной способности и ряда других факторов выбирается один из множества способов построения сети передачи данных.
Целью данной курсовой работы является проектирование автоматизированной системы резервирования мест и продажи билетов на автовокзале, основанное на построении сети передачи данных по заданной топологии. При этом на основании исходных данных производятся расчеты числа билетно-кассовых терминалов, времени реакции системы, а также определяются затраты на создание самой системы и рассматриваются вопросы техники безопасности и охраны труда.
1 Характеристика объекта проектирования
Рассматриваемый автовокзал находится в географическом центре города в 340 м от железнодорожного вокзала. Здание автовокзала двухэтажное: на первом этаже расположено девять билетных касс (из них одна касса возврата билетов), справочная служба, диспетчерская, помещение дежурного по вокзалу, здравпункт, зал ожидания, пункты общественного питания, камеры хранения, бытовые помещения, на втором этаже – административные помещения. В плане здание автовокзала занимает площадь 1000 м2.
Режим работы автовокзала с 5:30 до 23:30. Билетные кассы работают с 6:00 до 22:00. От платформ автовокзала отходят автобусы пригородного, междугороднего и международного сообщения. Всего насчитывается 73 маршрута.
Списочное количество сотрудников автовокзала составляет 62 человека.
Схема первого этажа автовокзала представлена в Приложении А задания.
2 Статистическая обработка исходных данных
Случайными называются явления (величины), исход (значение) или протекание которых при одинаковом комплексе условий заранее не предсказуем, однако при многократном их воспроизведении становится возможным заметить некоторые закономерности. Данные закономерности в дальнейшем подвергаются анализу, на основании которого можно выдвинуть гипотезу о законе распределения случайной величины. Последующие исследования подтверждают либо опровергают выдвинутую гипотезу.
Целью такого комплексного исследования случайного явления (величины) – статистической обработки данных – является использование полученных результатов для прогнозирования (предсказания) поведения данного явления и принятия соответствующих технических, организационных, управленческих и прочих решений в условиях неопределенности.
Статистическая обработка данных может осуществляться вручную (с использованием известных разработанных методик) и машинным способом (с использованием ЭВМ).
Исходные данные, представленные в Приложениях Б и В задания (соответственно, количество проданных билетов по дням года и количество справочных запросов), по своему смыслу относятся к случайным величинам. Таким образом, представляется целесообразным их статистическая обработка с целью дальнейшего эффективного использования результатов исследования. При этом данные из Приложения Б будут обработаны вручную, а данные из Приложения В – на компьютере с использованием программного обеспечения StatGraphicsPlusv5.0.1.
Первым шагом при статистической обработке данных является их упорядочение по возрастанию, т.е. построение вариационного ряда. Стоит отметить, что представленные исходные данные в Приложении Б – неубывающая последовательность, поэтому их упорядочения не требуется.
Второй шаг – группировка упорядоченных статистических данных. Стоит отметить, что представленные в Приложении Б данные являются дискретными величинами, однако из-за очень редкой повторяемости их значений по отношению к их количеству целесообразно группировать их как непрерывную случайную величину ξ – по интервалам.
С этой целью определяется количество интервалов одинаковой длины:
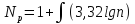 ,
(2.1)
,
(2.1)
где int– целая часть дробного числа;
n– объем выборки,n=365.
При этом
должно выполняться условие
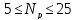 ,
иначе принимают значение соответствующей
границы условия.
,
иначе принимают значение соответствующей
границы условия.
Величину (длину) интервала определяют по следующей формуле:
 , (2.2)
, (2.2)
где
 – величина размаха исходных данных.
– величина размаха исходных данных.
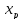 определяется по формуле:
определяется по формуле:
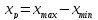 , (2.3)
, (2.3)
где 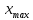 – максимальный элемент выборки;
– максимальный элемент выборки;
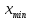 – минимальный элемент выборки.
– минимальный элемент выборки.
Границы интервалов определяются по следующим формулам:
верхняя:
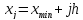 ; (2.4)
; (2.4)
нижняя:
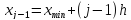 , (2.5)
, (2.5)
где j– номер интервала.
Середина интервалов определяется по формуле:
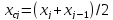 . (2.6)
. (2.6)
Относительная частота (вероятность) появления значений случайной величины ξ в интервале определяется по формуле:
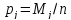 , (2.7)
, (2.7)
где 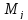 – частота появления значений случайной
величины в интервале, определяется
путем подсчета.
– частота появления значений случайной
величины в интервале, определяется
путем подсчета.
Ниже представлены расчеты по формулам (2.1)–(2.3):
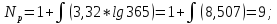
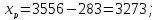
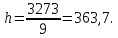
Расчет границ и относительной частоты по формулам (2.4)–(2.7) представлен для первого интервала:
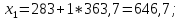


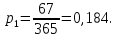
Дальнейшие расчеты сведены в таблицу 2.1.
Таблица 2.1 – Интервальный статистический ряд
|
Номер интервала |
Нижняя граница |
Верхняя граница |
Середина |
Частота
|
Относительная
частота
| ||
|
1 |
283 |
646,7 |
464,9 |
67 |
0,184 | ||
|
2 |
646,7 |
1010,4 |
828,6 |
118 |
0,323 | ||
|
3 |
1010,4 |
1374,1 |
1192,3 |
76 |
0,208 | ||
|
4 |
1374,1 |
1737,8 |
1556,0 |
35 |
0,096 | ||
|
5 |
1737,8 |
2101,5 |
1919,7 |
25 |
0,069 | ||
|
6 |
2101,5 |
2465,2 |
2283,4 |
23 |
0,063 | ||
|
7 |
2465,2 |
2828,9 |
2647,1 |
11 |
0,030 | ||
|
8 |
2828,9 |
3192,6 |
3010,8 |
7 |
0,019 | ||
|
9 |
3192,6 |
3556,3 |
3374,5 |
3 |
0,008 | ||
|
Сумма: |
365 |
1,000 | |||||
На основании данных таблицы 2.1 строится гистограмма (рисунок 2.1), наглядно представляющая статистический ряд.
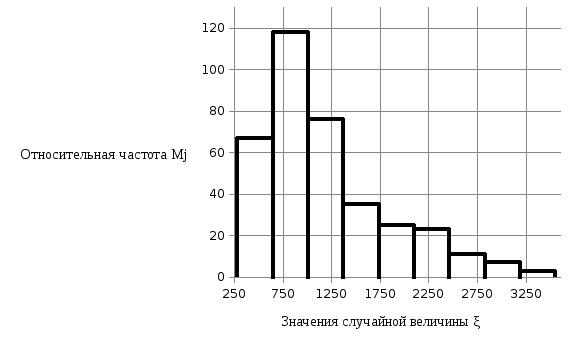
Рисунок 2.1 – Гистограмма статистического ряда
На рисунке 2.2 представим эмпирическую функцию плотности распределения f’(x)случайной величины ξ, а на рисунке 2.3 – эмпирическую функцию распределенияF’(x).
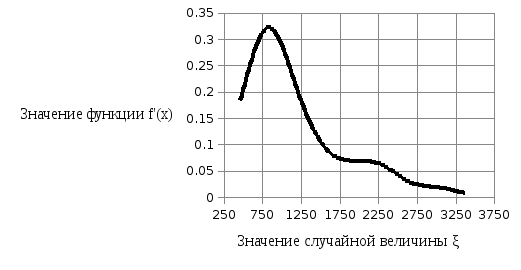
Рисунок 2.2 – Эмпирическая функция плотности распределения f’(x)случайной величины ξ

Рисунок 2.3 – Эмпирическая функция распределения F’(x)случайной величины ξ
Анализируя рисунки 2.1–2.3, можно выдвинуть гипотезу Hoо логарифмически-нормальном законе распределения случайной величины ξ, характеризующей количество проданных билетов. Альтернативная гипотезаHaзаключается в том, что случайная величина ξ не распределяется по логарифмически-нормальному закону.
Функция плотности гипотетического распределения f(x)случайной величины ξ, распределенной по логарифмически-нормальному закону, определяется по формуле:
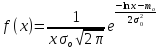 , (2.8)
, (2.8)
где 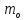 – математическое ожидание логарифма
случайной величины ξ;
– математическое ожидание логарифма
случайной величины ξ;
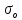 – среднеквадратическое отклонение
логарифма случайной величины ξ;
– среднеквадратическое отклонение
логарифма случайной величины ξ;
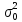 – дисперсия логарифма случайной величины
ξ.
– дисперсия логарифма случайной величины
ξ.
Математическое
ожидание логарифма случайной величины
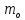 определяется по следующей формуле:
определяется по следующей формуле:
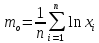 . (2.9)
. (2.9)
Среднеквадратическое
отклонение
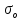 логарифма случайной величины ξ
определяется по формуле:
логарифма случайной величины ξ
определяется по формуле:
 . (2.10)
. (2.10)
Дисперсия
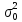 логарифма случайной величины ξ
рассчитывается по формуле:
логарифма случайной величины ξ
рассчитывается по формуле:
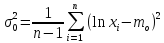 . (2.11)
. (2.11)
Математическое
ожидание
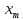 определяется по следующей формуле:
определяется по следующей формуле:
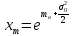 . (2.12)
. (2.12)
Среднеквадратическое
отклонение
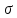 определяется по формуле:
определяется по формуле:
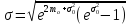 . (2.13)
. (2.13)
Коэффициент вариации рассчитывается по формуле:
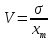 . (2.14)
. (2.14)
Функция распределения F(x)случайной величины ξ определяется по формуле:
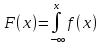 . (2.15)
. (2.15)
Проверка
выдвинутой гипотезы будет производиться
на основании критерия «значимости»
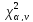 Пирсона. Здесьα– уровень значимости
статистического критерия;v– число степеней свободы, которое
определяется по формуле:
Пирсона. Здесьα– уровень значимости
статистического критерия;v– число степеней свободы, которое
определяется по формуле:
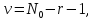 (2.16)
(2.16)
где 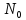 – количество интервалов статистического
ряда после его преобразования;
– количество интервалов статистического
ряда после его преобразования;
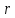 – количество параметров функции
гипотетического распределения,
– количество параметров функции
гипотетического распределения,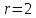 .
.
Уровень значимости αстатистического критерия – вероятность совершения ошибки 1-го рода, т.е. вероятность отклонения верной нулевой гипотезыHo. Примем значение уровня значимостиα=0,025.
При проверке
выдвинутой гипотезы критическое значение
 сравнивается с выборочным значением
статистического критерия значимости
сравнивается с выборочным значением
статистического критерия значимости ,
рассчитанным по формуле:
,
рассчитанным по формуле:
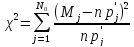 , (2.17)
, (2.17)
где 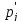 – теоретическая вероятность попадания
вj-ый интервал случайной
величины ξ, распределенной по
гипотетическому закону распределения.
– теоретическая вероятность попадания
вj-ый интервал случайной
величины ξ, распределенной по
гипотетическому закону распределения.
Если значение
 меньше
меньше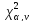 ,
то выдвинутая гипотеза считается верной.
,
то выдвинутая гипотеза считается верной.
Теоретическая
вероятность
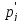 для логарифмически-нормального
распределения определяется через
функцию Лапласа
для логарифмически-нормального
распределения определяется через
функцию Лапласа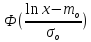 по формуле:
по формуле:
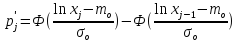 . (2.18)
. (2.18)
Значения функции Лапласа выбираются по специальным таблицам. При этом следует помнить, что функция Лапласа нечетная.
Также следует выполнить ряд преобразований статистического ряда распределения:
интервалы, частота Mjкоторых меньше 5, объединяются с одним из ближайших интервалов;
нижняя граница крайнего левого интервала принимает значение минус ∞, а верхняя граница крайнего правого интервала – плюс ∞.
Таким образом, преобразованный статистический ряд принимает следующий вид (таблица 2.2).
Таблица 2.2 – Преобразованный статистический ряд
|
Номер интервала |
Нижняя граница |
Верхняя граница |
Середина |
Частота
|
Относительная
частота
| ||
|
1 |
-∞ |
646,7 |
– |
67 |
0,184 | ||
|
2 |
646,7 |
1010,4 |
828,6 |
118 |
0,323 | ||
|
3 |
1010,4 |
1374,1 |
1192,3 |
76 |
0,208 | ||
|
4 |
1374,1 |
1737,8 |
1556,0 |
35 |
0,096 | ||
|
5 |
1737,8 |
2101,5 |
1919,7 |
25 |
0,069 | ||
|
6 |
2101,5 |
2465,2 |
2283,4 |
23 |
0,063 | ||
|
7 |
2465,2 |
2828,9 |
2647,1 |
11 |
0,030 | ||
|
8 |
2828,9 |
+∞ |
– |
10 |
0,027 | ||
|
Сумма: |
365 |
1,000 | |||||
Далее производится расчет по формулам (2.9)–(2.14) и (2.16) (расчет по формулам (2.9) и (2.11) произведен с использованием программы MicrosoftExcel):
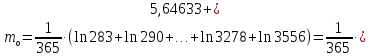
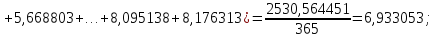
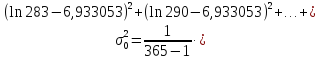
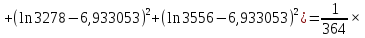
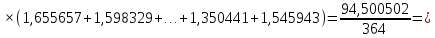
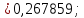
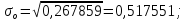
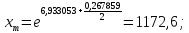
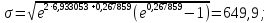


По формуле (2.18) производится расчет для первого интервала:
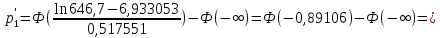

Дальнейшие расчеты сведены в таблицу 2.3.
Таблица 2.3
– Расчет
теоретических частот
|
Номер интервала |
Нижняя граница |
Верхняя граница |
Теоретическая
частота
| |
|
1 |
-∞ |
646,7 |
0,1867 | |
|
2 |
646,7 |
1010,4 |
0,3053 | |
|
3 |
1010,4 |
1374,1 |
0,2203 | |
|
4 |
1374,1 |
1737,8 |
0,1315 | |
|
5 |
1737,8 |
2101,5 |
0,0724 | |
|
6 |
2101,5 |
2465,2 |
0,0383 | |
|
7 |
2465,2 |
2828,9 |
0,0205 | |
|
8 |
2828,9 |
+∞ |
0,025 | |
|
Сумма: |
1,0000 | |||
На основании
данных таблицы 2.3 по формуле (2.17)
рассчитывается выборочное значение
статистического критерия значимости
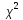 :
:

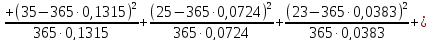
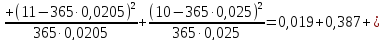
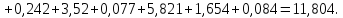
Критическое
значение
 критерия «значимости» Пирсона больше
расчетного
критерия «значимости» Пирсона больше
расчетного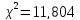 .
Таким образом, выдвинутая гипотеза о
логарифмически-нормальном распределении
случайной величины ξ, характеризующей
количество продаваемых в день билетов,
считается верной и принимается для
дальнейших расчетов.
.
Таким образом, выдвинутая гипотеза о
логарифмически-нормальном распределении
случайной величины ξ, характеризующей
количество продаваемых в день билетов,
считается верной и принимается для
дальнейших расчетов.
Статистическая обработка данных Приложения В выполнена с помощью программного обеспечения StatGraphicsPlusv5.0.1. Результаты обработки представлены в Приложении Г.
Данные Приложения Г позволяют сделать вывод о равномерном распределении случайной величиной, характеризующей количество справочных запросов в день.