6.2.4 Численное дифференцирование на основе интерполяционной формулы Ньютона

Запишем для функции f(x), заданной своими значениями в равноотстоящих узлахпервый интерполяционный многочлен Ньютона:

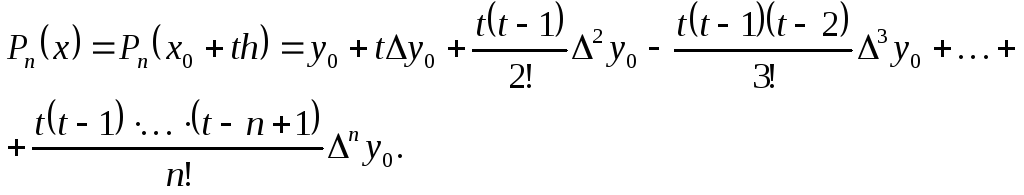
Перепишем этот полином, производя перемножение скобок:

Дифференцируя поt, получим аналогично формуле (6.16):

(6.21)

Подобным путем можно получить и производные функции f(x)более высоких порядков. Однако каждый раз, вычисляя значение производной функцииf(x) в фиксированной точкех, в качествех₀следует брать ближайшее слева узловое значение аргумента.

Формула (6.21) существенно упрощается, если исходным значением хоказывается один из узлов таблицы. Так как в этом случае каждый узел можно считать начальным, то принимаях=х_0, t=0, получаем:

(6.22)

Эта формула позволяет точно получать значения производных функций, заданных таблично.

Выведем формулу погрешности дифференцирования. Используя формулу (6.17) применительно к первому интерполяционному многочлену Ньютона, запишем:

где ‑ промежуточное значение междуи заданной точкойх. Предполагая, чтоf(x) дифференцируемап+1 раз, получим для оценки погрешности дифференцирования(по аналогии с формулой (6.18)):

(6.23).

Для случая оценки погрешности в узле таблицы получим:

.

На практике оценивать непросто, поэтому при малыхh приближенно полагают:

Что позволяет использовать приближенную формулу

(6.24).

6.2.5 Постановка задачи численного интегрирования

При вычислении определенного интеграла

где f(x) – непрерывная на отрезке [a;b] функция, иногда удается воспользоваться формулой Ньютона-Лейбница:

(6.25).

Здесь F(x) – одна из первообразных функцииf(x). Однако даже в тех редких случаях, когда первообразную удается явно найти в аналитической форме, не всегда удается довести до числового ответа значение определенного интеграла. Если учесть, что подынтегральная функция задается таблицей или графиком, то интегрирование по формуле (6.24) не получает широкого применения на практике.

В подобных случаях применяют различные методы численного интегрирования. Формулы, используемые для вычисления однократных интегралов, называют квадратурными формулами.

Прием построения квадратурных формул состоит в том, что подынтегральная функция f(x) заменяется на отрезке [a;b] интерполяционным многочленом, например, многочленом Лагранжа, и получается приближенное равенство

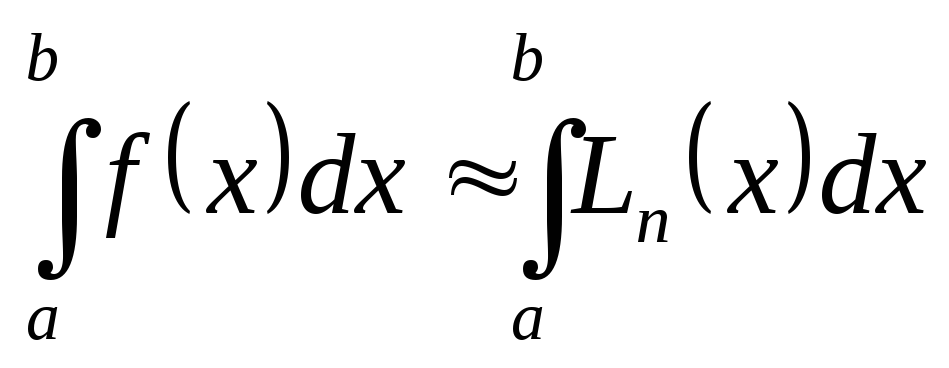(6.26)

Предполагается, что отрезок [a;b] разбит нап частей точками, наличие которых подразумевается при построении многочлена.

Подставляя вместо (6.10), получим

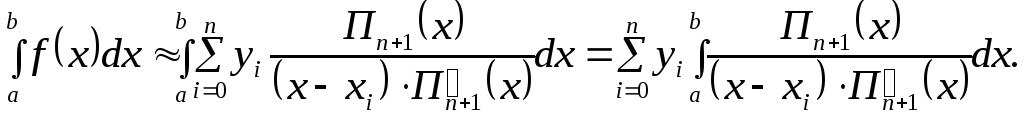
Таким образом,

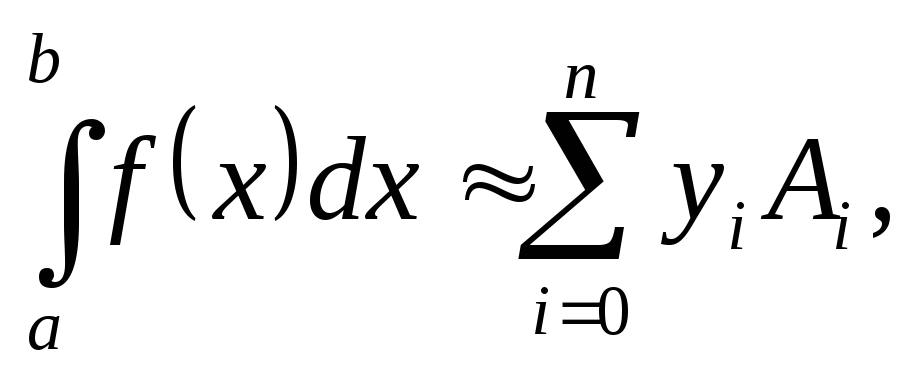(6.27)

где 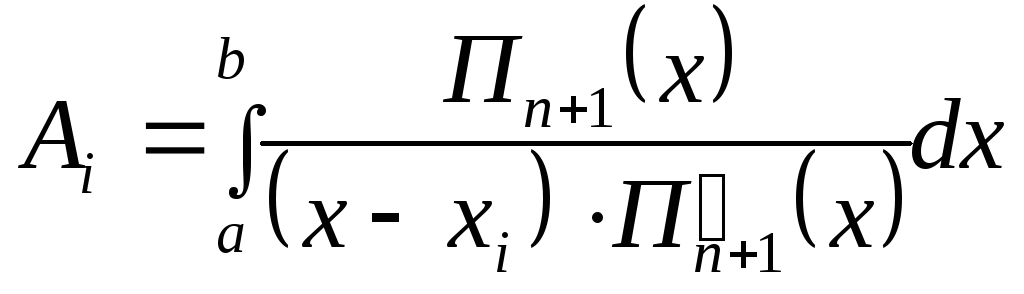(6.28)

В формуле (6.27) коэффициенты не зависят от функцииf(x), так как они составлены только с учетом узлов интерполяции; еслиf(x)– полином степенип, то формула (6.27) точная, так как.

6.2.6 Квадратурные формулы Ньютона-Котеса

Применение формулы (6.26) предполагает построение на отрезке интегрирования [a;b] системы узлов интерполяции, которыми отрезок делится напчастей. Длина _{, называется шагом интегрирования. Естественно считать, что шаг h постоянен, т.е.}

.

В этом случае можно применить интерполяционную формулу Лагранжа для равноотстоящих узлов. Итак, с учетом (6.12) и (6.14) формула (6.28) для весовых коэффициентов A_i примет вид:

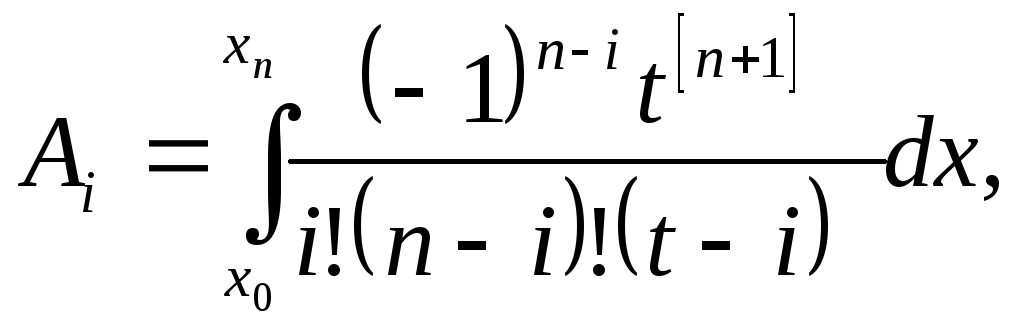
_(6.29)

Перейдем в этом интеграле к переменной t. Из подстановки (6.9) получаем:

_т.е.

_{При х=х0 имеем t=0, а при х=хn будет}

Тогда

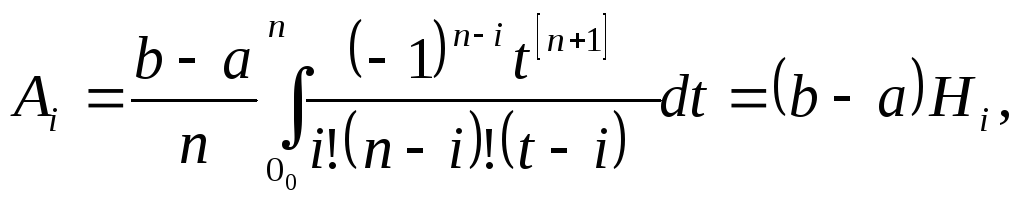_(6.30)

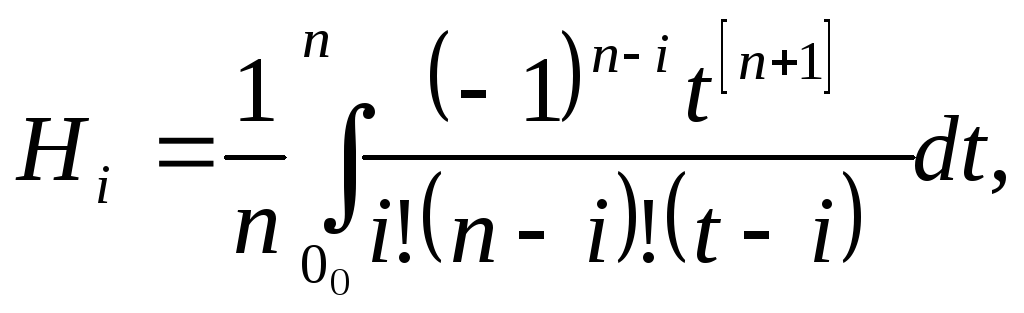
где _(6.31)

_{Числа (6.29) называют коэффициентами Котеса. Они не зависят от функции f(х), а только от числа точек разбиения. Окончательно, с учетом формул (6.27) и (6.30) получаем следующий вид квуадратурных формул формул Ньютона-Котеса:}

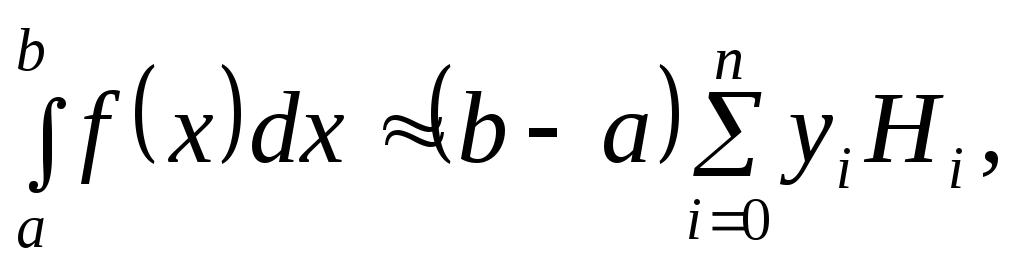_(6.32)

дающих на одном участке интегрирования различные представления различного числа потрезков разбиения.