Разряд конденсатора в цепи, состоящей из сопротивления и катушки индуктивности

На рис. 2 изображена схема электрической цепи, состоящей из конденсатора С, сопротивления R и катушки индуктивности L.

Соединив ключом клеммы 1 – 3, зарядим конденсатор до напряжения . Если теперь ключом соединить клеммы 2 – 3, конденсатор начнет разряжаться через сопротивление R и катушку индуктивности L. При разряде конденсатора в катушке индуктивности возникает э.д.с. самоиндукции, величина которой с течением времени, пока длится разряд конденсатора, будет изменяться.

1 2

3

L

Е С

R

Рис. 2

Запишем второй закон Кирхгофа для данной цепи:

Заменив в этом уравнении , получим дифференциальное уравнение 2 – го порядка:

(6)

Решение этого уравнения имеет вид:

(7)

График этой функции имеет вид:

Анализируя это выражение, можно прийти к следующим заключениям:

1. При разряде конденсатора в цепи, содержащей R, L и C, величина напряжения на обкладках конденсатора совершает затухающие колебания.

2. Величина называется коэффициентом затухания.

3. Амплитуда затухающих колебаний напряжения изменяется по закону

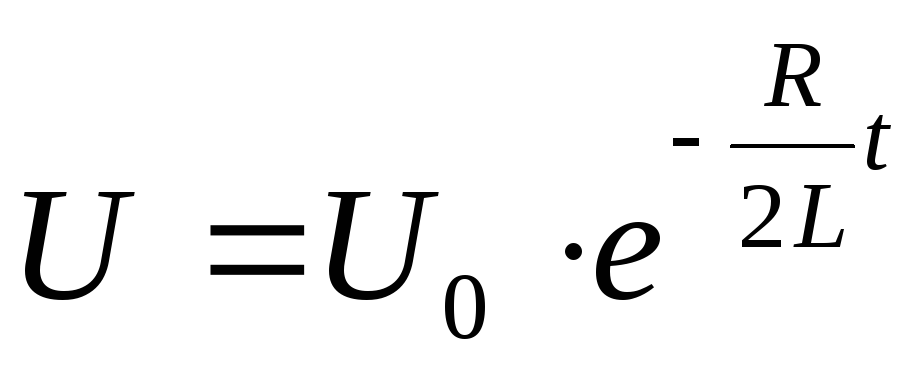
4. Циклическая частота затухающих колебаний меньше собственной частотыи равна:

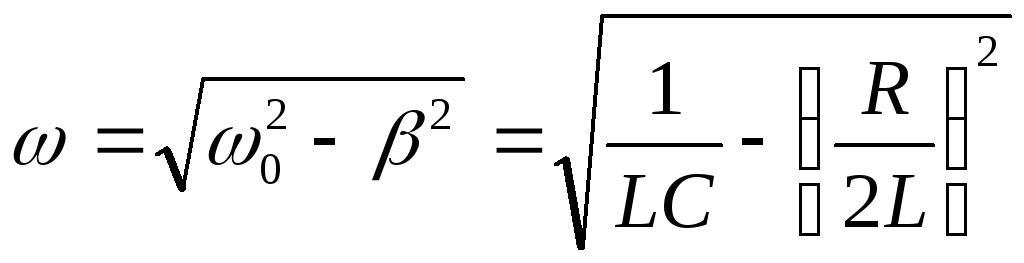
5. Период затухающих колебаний:

С увеличением сопротивления R контура период Т возрастает, а при обращается в бесконечность.

Если , то изменение напряжения на обкладках не носит колебательный характер, и напряжение монотонно уменьшается до нуля. Такой разряд конденсатора называется апериодическим, т.к. в этом переходном процессе не происходит перезарядки конденсатора.

Сопротивление контура, при котором колебательный процесс переходит в апериодический, называется критическим.

Значение критического сопротивления определяется условием: , т.е., отсюда

Если , то разряд конденсатора в цепи будет представлять собой колебательный процесс, связанный с периодической перезарядкой пластин конденсатора. Как величина напряжения на конденсаторе, так и величина тока в цепи будут совершать затухающие колебания.

Затухание колебаний принято характеризовать логарифмическим декрементом затухания . Логарифмический декремент затухания равен натуральному логарифму отношения амплитуд двух колебаний, измеренных через промежуток времени, равный периоду Т:

Логарифмический декремент затухания обратен по величине числу колебаний N, совершенных за время, в течение которого амплитуда уменьшится в раз:

Если вторичное измерение амплитуды напряжения производится через периодов после первого измерения, то

Задание 1.

Исследование разряда конденсатора в цепи, содержащей сопротивление. Определение электроемкости конденсатора.

Порядок выполнения работы

1. Собрать электрическую цепь по схеме, изображенной на рисунке 3.

K 1 2 3

ЭО

+

Е С R

_

y

Рис. 3

2. Используя магазин сопротивлений, установить сопротивление порядка 90 – 100 Ом с тем, чтобы на экране получилась кривая, изображающая падение напряжения при разряде конденсатора, происходящее за времяс. (рис 4). За это время конденсатор не должен полностью разрядиться.

U

Рис. 4

3. Измерить по шкале на экране начальную () и конечную () ординаты этой кривой. Длины этих ординат пропорциональны начальному напряжениюи напряжению, которое остается на конденсаторе черезс после начала разряда:

Логарифмируя это выражение, получим:

, отсюда

4. Вычислить постоянную времени .

5. Рассчитать электроемкость конденсатора по формуле

6. Повторить опыты, меняя сопротивление .

Задание 2. Исследование разряда конденсатора в цепи, содержащий сопротивление и катушку индуктивности.