
- •Функціональні навантаження виконавців посібника
- •Анотація
- •В и м о г и д о о ф о р м л е н н я з а в д а н ь розрахунково-графічної роботи
- •Буквені позначення основних величин теоретичної механіки
- •Короткі відомості з теорії і методичні вказівки, необхідні для виконання завдання д-16 Застосування принципу Даламбера до визначення реакцій в’язей
- •План розв’язання задач за допомогою принципу Даламбера
- •Приклади виконання завдання д-16
- •Короткі відомості з теорії і методичні вказівки, необхідні для виконання завдання д-15 Застосування принципу можливих переміщень до визначення реакцій опор складеної конструкції
- •Приклади виконання завдання д-15
- •Короткі відомості з теорії і методичні вказівки, необхідні для виконання завдання д-19 Застосування загального рівняння динаміки до дослідження руху механічної системи з одним ступенем вільності
- •План розв’язання задач за допомогою загального рівняння динаміки
- •Приклад виконання завдання д-19.
- •Короткі відомості з теорії і методичні вказівки, необхідні для виконання завдання д-23 Дослідження вільних коливань механічної системи з одним ступенем вільності
- •Основні властивості малих вільних коливань
- •Приклад виконання завдання д-23
- •Література
- •Методичний посібник
Короткі відомості з теорії і методичні вказівки, необхідні для виконання завдання д-15 Застосування принципу можливих переміщень до визначення реакцій опор складеної конструкції
1. Можливим переміщенням механічної системи називається будь-яка сукупність нескінченно малих переміщень точок системи, які допускаються в даний момент усіма накладеними на систему в’язями.
Можливі переміщення повинні задовольняти двом умовам:
- вони повинні бути нескінченно малими, тому що при кінцевих переміщеннях система перейде в інше положення, де умови рівноваги можуть бути іншими;
- вони повинні бути такими, щоб всі накладені в даний момент часу на систему в’язі зберігалися, інакше може змінитися вид розглядуваної механічної системи.
При стаціонарних в’язях,
тобто в’язях, які не залежать від часу,
дійсне переміщення
![]() збігається з одним з можливих переміщень
збігається з одним з можливих переміщень![]() .
.
При нестаціонарних в’язях
дійсне переміщення
![]() не збігається з жодним з
можливих переміщень.
не збігається з жодним з
можливих переміщень.
2. Число незалежних між собою можливих переміщень механічної системи називається числом ступенів вільності цієї системи.
Число ступенів вільності для тіла, або системи тіл, визначається як різниця між числом рівнянь рівноваги в вибраній декартовій системі координат для всіх тіл системи і числом накладених в’язей.
Для плоского розташування тіл і системи сил:
S=3n-k. (1)
Для просторового розташування тіл і системи сил:
S=6n-k, (2)
деS– число ступенів вільності системи;
n - число тіл в системі;
k – число накладених в’язей.
3. Можливою роботою сили називається робота сили на одному з можливих переміщень точки її прикладання:
![]() (3)
(3)
Ідеальноюназивається в’язь, сума робіт сил реакцій якої на будь-якому можливому переміщенні точок системи дорівнює нулю, тобто:
![]() або
або
![]() . (4)
. (4)
де
![]() –
реакція в’язі, що діє наi-ту
точку системи;
–
реакція в’язі, що діє наi-ту
точку системи;
![]() –можливе переміщення i-тої
точки системи;
–можливе переміщення i-тої
точки системи;
n– число матеріальних точок системи.
Якщо сума можливих робіт реакцій в’язей відрізняється від нуля, то в’язь називається неідеальною
4. Принцип можливих переміщень формулюється так: для рівноваги механічної системи з утримуючими стаціонарними ідеальними в’язями необхідно і достатньо, щоб алгебраїчна сума можливих робіт всіх активних сил, прикладених до системи, на будь-якому можливому переміщенні системи дорівнювала нулю:
![]() (5)
(5)
Умову рівноваги механічної системи називають також рівнянням можливих робіт.
5.Принцип можливих переміщень ефективний при розв’язуванні задач про рівновагу системи твердих тіл. Такі системи не мають жодного ступеня вільності. Якщо треба визначити яку-небудь реакцію ідеальної в’язі, то слід, застосовуючи принцип звільнення від в’язей, відкинути відповідну в’язь і замінити її дію шуканою реакцією в’язі, яку в подальшому вважаємо активною силою. При цьому механічна система, що звільнена від однієї в’язі, отримує один ступінь вільності.
Надають системі можливе переміщення, яке відповідає цьому ступеню вільності і встановлюють зв'язок між можливими переміщеннями тіл системи.
Складають рівняння можливих робіт усіх сил (заданих сил і шуканої сили реакції в’язі) на відповідних можливих переміщеннях точок їх прикладання і цю суму прирівнюють до нуля. З отриманого рівняння визначають шукану реакцію.
В’язі і еквівалентні їм схеми в’язей і реакції
|
№пп |
Вид в’язі |
Е |
|
1 |
Жорстке защемлення .
|
|
|
| ||
|
|
|
2 |
Нерухомий циліндричний шарнір
|
|
|
| ||
|
3 |
Р
|
|

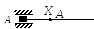 квівалентна
схема в’язі і реакції
квівалентна
схема в’язі і реакції

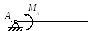

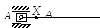
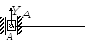
 ухомий
циліндричний шарнір
ухомий
циліндричний шарнір