Приклади виконання завдання д-16
Задача 1.
Визначити реакції зовнішніх в’язей механічної системи.
|
M
А 0
R 2
B 60 1 Рис. 1 |
Дано: схема системи (рис.1). Маси тіл системи: m1 =100 кг,m2=40 кг. Радіус тіла 2: R=0,1 м. Тіло 2 вважати однорідним циліндром. Обертальний момент: M=110 Н·м. Вагою стержнів ОА і ОВ знехтувати. |
|
|
Розв’язання(рис.2)
1.Покажемо на рисунку зовнішні
сили, прикладені до механічної системи:
сили ваги
2 Покажемо на схемі прискорення тіла 1 і кутове прискорення тіла 2
3 Прикладемо до тіла 1 силу
інерції
|
і
;
обертальний момент М;
зусилля в стержнях
і
.
,
а до тіла 2 - головний момент сил інерції
і знайдемо їх модулі:
, 
.
,
4. Система координат показана на рис.2
5. Складемо рівняння рівноваги отриманої довільної плоскої системи сил:
,
, (1)
,
, (2)
,
(3)
6. Розв’яжемо отриману систему рівнянь і знайдемо шукані величини:
з рівняння (3):
,
м/с
з рівняння (2): 
Н.
з рівняння (1): 
Н.
Відповідь: 
=
2549,5 Н (стержень ОА
- розтягнутий),
=
-2944 Н (стержень ОВ
- стиснутий).
Задача 2.
Визначити реакції зовнішніх в’язей механічної системи, що зображена на рис.1.
|
|
Дано: ОА– однорідний стержень. Маса стержня : m=20 кг. Довжина стержня: l= 0,6 м. В точці О – кульовий шарнір.
|
|
рис.2 Розв’язання.(рис.2)
1. Покажемо на схемі зовнішні
сили, що діють на стержень ОА:
силу ваги
2. Диференціальне рівняння обертального руху стержня навколо осі Оz має вид:
Звідси випливає, що
3. Прискорення центра мас стержня (точки С):
| |
|
|
4. Головний вектор сил інерції:
5. Прискорення кожної точки стержня напрямлено до осі обертання Оz і змінюється від нуля (в точці О) до максимального значення (в точці А). Отже, і сили інерції кожної точки стержня змінюються від нуля до максимального значення і напрямлені проти векторів прискорення точок стержня. Тобто, маємо лінійно розподілену систему сил інерції яку можна замінити зосередженою силою (рис.2). |
і реакції кульового
шарніра
і
(рис.2).
.
,
.
.
,
.Згідно з принципом Даламбера ми отримали зрівноважену систему сил до якої можна застосувати рівняння статики.
6. Складемо рівняння рівноваги отриманої довільної плоскої системи сил (рис.2).
,
, (1)
,
, (2)
,
(3)
7. Розв’яжемо отриману систему рівнянь і знайдемо шукані величини:
з рівняння (3)
Н,
,
рад/с,
з рівняння (1) 
Н,
з рівняння (2) 
Н.
Відповідь:
=
-84,9 Н, 
=
-196Н.
Зауваження.
Положення точки прикладення
сили
можна
було визначити з таких міркувань:
оскільки сума моментів паралельних сил
інерції точок стержня відносно точкиО
дорівнює рівнодійній цих сил (рис.2 і
рис.3), то
, (4)
деh–
плече сили
відносно точки О
(рис.2);
–
сила інерції елемента стержня довжиною
;
– координата елемента стержня (рис.3);
|
|
Підстановка в рівняння (4):
|
,
деdm–
маса елемента стержня довжиною
.
Звідки:
Порівняйте результат з
показаним на рис.2.
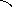