конспекты / 123

Лекция 9. Взаимное пересечение поверхностей

∙Взаимное пересечение поверхностей. Общие положения.

∙Пересечение двух многогранников.

∙Пересечение гранной и кривой поверхности.

∙Пересечение двух кривых поверхностей. Метод вспомогательных секущих плоскостей.

∙Пересечение поверхностей вращения. Метод вспомогательных секущих сфер.

∙Теорема Монжа.

Взаимное пересечение поверхностей

Общие положения

При пересечении поверхностей образуется линия, которую принято называть линией взаимного пересечения поверхностей. Эта линия пересечения принадлежит одновременно двум поверхностям. Поэтому построение линии пересечения сводится к определению точек одновременно принадлежащих обеим поверхностям. Для нахождения таких точек использу-

ется в общем случае метод вспомогательных секущих поверхностей. Сущность способа за-

ключается в следующем: Пусть задано две поверхности σ и ψ (рисунке 9.1)

Общий алгоритм построе-

ния линии пересечения поверхно-

стей:

1. Введем вспомогатель-

ную поверхность Ф.

2. Строим линии пересе-

чения поверхности Ф с поверхно-

стями σ и ψ (a и b).

Рисунок 9.1

3. Определяем точки пере-

сечения К и М, построенных линий пересечения a и b.

4.Многократно повторяя эту операцию, найдем ряд точек, принадлежащих одно-

временно двум поверхностям.

5.Соединяем последовательно точки с учетом видимости.

В качестве посредников могут быть приняты как поверхности, так и плоскости, но це-

лесообразно выбирать такие, которые дают наиболее простые линии пересечения с заданны-

ми поверхностями.

60

кает поверхность пирамиды. Для определения точек пересечения 5 и 6 через ребро DD' про-

водим горизонтальную плоскость, которая пересекает пирамиду по треугольнику. Точки 5 и 6 получаем, как пересечение DD' с построенным треугольником.

Полученные точки соединяем с учетом видимости. Видимой считается тот отрезок прямой, который принадлежит двум видимым граням поверхностей.

Как видим, линия пересечения двух многогранников представляет собой простран-

ственную ломаную линию.

В том случае, когда обе гранные поверхности общего положения, последовательность соединения точек вызывает затруднение. Поэтому для соединения точек используется диа-

грамма Ананова – условные развертки поверхностей (см. учебник).

Пересечение гранной и кривой поверхности

Линия пересечения гранной и кривой поверхности, представляет собой простран-

ственную кривую линию, с точками излома на ребрах многогранника.

61

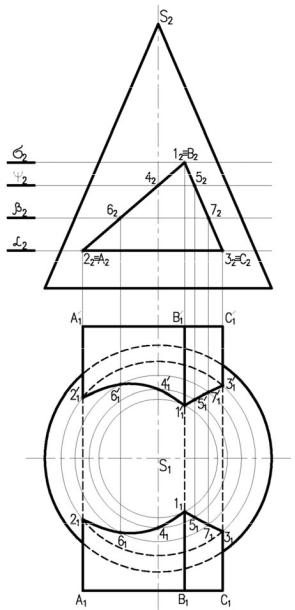
Поэтому сначала определяем точки пе-

ресечения ребер многогранника с кривой по-

верхностью, а затем промежуточные точки и соединяем их с учетом видимости. На рисунке

9.3 заданы поверхности трехгранной призмы и кругового конуса.

Так как призма фронтально-

проецирующая, фронтальная проекция линии пересечения совпадает с проекцией боковых граней призмы, поэтому необходимо постро-

ить только горизонтальную проекцию линии пересечения.

Сначала определяем точки пересечения ребер призмы АА', ВВ', СС' с поверхностью конуса, а затем находим промежуточные точ-

ки, принадлежащие линиям пересечения. Для нахождения точек пересечения, используем горизонтальные плоскости посредники, так как они пересекают конус по окружностям, а

призму по прямым линиям. Как видим, в дан-

ном случае линия пересечения распадается на две отдельные части.

Рисунок 9.3

Пересечение двух кривых поверхностей

Метод вспомогательных секущих плоскостей

Линия пересечения двух кривых поверхностей, представляет пространственную кри-

вую линию. Поэтому для ее построения необходимо определить ряд точек принадлежащих этой лини.

На рисунке 9.4 заданы поверхности конуса и сферы. Точки строятся при помощи го-

ризонтальных плоскостей посредников, которые рассекают обе поверхности по окружно-

стям.

Обязательно находим опорные точки, к которым относятся высшая и низшая точки линии пересечения и точки границы видимости. Так как оси поверхностей лежат в одной

62

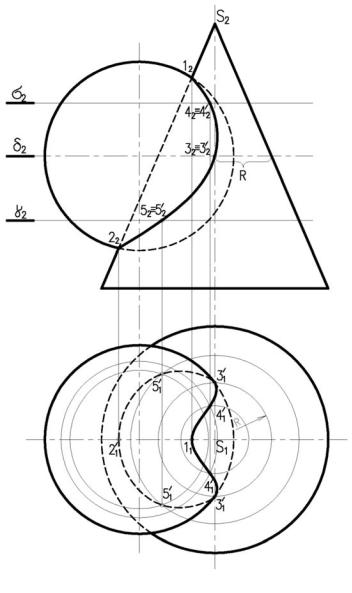
фронтальной плоскости, контурные образующие поверхностей пересека-

ются в точках 1 и 2 – это и будет выс-

шая и низшая точки. Точки границы видимости лежат на экваторе сферы,

поэтому точки 3 и 3' находим с помо-

щью вспомогательной горизонтальной плоскости, проходящей через центр сферы. Она рассекает сферу по эква-

тору, а конус по параллели радиуса R.

Взаимно пересекаясь, они и дают точки 3 и 3' фронтальную проек-

цию определяем по вертикальной ли-

нии связи на плоскости δ. Затем берем еще две вспомогательные плоскости расположенные выше и ниже плоско-

сти δ и выполняя, аналогичные по-

строения определяем точки 4 и 4', 5 и 5'. Полученные точки соединяем с учетом видимости.

Рисунок 9.4

Пересечение поверхностей вращения

Метод вспомогательных секущих сфер

Способ вспомогательных секущих сфер применяется при следующих условиях:

1.Пересекающиеся поверхности являются поверхностями вращения.

2.Оси этих поверхностей пересекаются.

3.Оси поверхностей параллельны одной из плоскостей проекций.

Перед рассмотрением этого способа разберем понятие соосных поверхностей. Соос-

ными называются поверхности вращения, имеющие общую ось. Соосные поверхности пере-

секаются по окружностям перпендикулярным оси вращения.

На рисунке 9.5 приведены некоторые из них.

Именно то, что поверхности пересекаются по окружностям, которые проецируются в линии и используется в методе сфер.

63

Рисунок 9.5

Рассмотрим пример на рисунок 9.6. Даны поверхности вращения – конус и цилиндр.

Так как оси лежат в одной плоскости, можно определить точки пересечения контурных обра-

зующих в точках 1 и 2, как в предыдущем примере.

Однако, для нахождения промежуточных точек, вспомогательные секущие плоскости не подходят, т.к. горизонтальные плоскости рассекут цилиндр по эллипсам, фронтально-

проецирующие – конус по эллипсам. А сам эллипс строить непросто. Поэтому именно в этом случае удобно использовать в качестве посредников – сферы. За центр вспомогательных сфер, принимается точка пересечения осей заданных поверхностей. Далее необходимо опре-

делить, размеры радиусов вспомогательных секущих сфер. Максимальный радиус сферы

рем вспомогательные сферы радиусов в пределах от Rmin до Rmax.

Они пересекают и поверхность цилиндра, и поверхность конуса по окружностям, ко-

торые пересекаясь дают промежуточные точки. Полученные точки соединяются плавной ли-

нией.

Здесь построена только фронтальная проекция. Для построения горизонтальной про-

екции, если это необходимо, точки строят как лежащие на окружностях полученных радиу-

сов.

Теорема Монжа

Рассмотрим вариант, когда минимальная сфера касается двух поверхностей вращения.

В этом случае для построения линии пересечения поверхностей используется теорема Г.Монжа, которая формулируется так:

Если две поверхности вращения второго порядка описаны около третьей или

вписаны в нее, то линия их пересечения распадается на две плоские кривые второго

порядка. Плоскости этих кривых проходят через прямую, соединяющую точки пересе-

чении линий касания.

В соответствии с этой теоремой линии пересечения конуса и цилиндра описанно-

го около сферы (рисунок 9.7)

будут плоскими кривыми – эллипсами, фронтальные про-

екции которых изображаются прямыми 1242 и 2232, прохо-

дящими через 5252' – точки линий пересечения окружно-

стей касания.

Рисунок 9.7

65

Лекция 10. Развертка поверхностей

∙Развертка поверхностей. Общие сведения.

∙Построение разверток развертываемых поверхностей: способом триангуляции,

способом раскатки, способом нормального сечения.

∙Построение приближенной развертки неразвертываемых поверхностей.

∙Решение задач.

Развертка поверхностей

Общие сведения

Разверткой поверхности называется плоская фигура, полученная путем совмеще-

ния элементов поверхности с плоскостью.

Если для поверхности можно построить её развертку точно без складок и разрывов,

то поверхность называется развертываемой, в противном случае – неразвертываемой .

К развертываемым поверхностям относятся все гранные, а из линейчатых только – цилиндрические, конические и поверхности с ребром возврата.

Построение разверток развертываемых поверхностей

Существуют следующие способы построения разверток развертываемых поверхно-

стей:

1.Способ триангуляции (треугольников);

2.Способ раскатки;

3.Способ нормального сечения.

Способ триангуляции (треугольников) применяется для построения разверток пи-

рамидальных и конических поверхностей. Они выполняются по одному принципу. Каждая грань пирамиды представляет треугольник и для построения развертки необходимо опреде-

лить натуральные величины всех сторон треугольника. По найденным натуральным вели-

чинам сторон вычерчиваются последовательно треугольные грани. Коническая поверх-

ность, заменяется вписанной в нее, пирамидальной и решение задачи ведется аналогично пирамиде.

Рассмотрим пример, построения развертки, конической поверхности (рисунок 10.1)

Для построения развертки в конус вписываем двенадцатигранную пирамиду. Т.к. по условию конус расположен симметрично относительно оси, построим половину развертки.

66

Образующие конуса имеют разную длину, поэтому натуральную величину определяем вращением до положения параллельного фронтальной плоскости проекций. Только образующие S1 и S7,

проецируются в натуральную величину. По полученным нату-

ральным величинам образующих и размерам хорд окружности основания, между образующими, строим половину развертки,

состоящую из шести треугольников вписанной в конус пира-

миды. Точки основания соединяем плавной кривой линией.

Рисунок 10.1

Способ раскатки применяется для построения разверток призматической и цилин-

дрической поверхности. И если поверхность цилиндрическая, то в нее вписывается призма-

тическая поверхность. Поэтому принцип построения этих разверток одинаков.

Рассмотрим пример построения развертки наклонной треугольной призмы (рисунок

10. 2)

Развертку можно выполнять только в том случае, если боковые ребра призмы парал-

лельны плоскости проекций, как на рисунке 10.2. В противном случае, сначала выполняется преобразование (методом замены строится новая проекция на плоскость параллельную реб-

рам). При выполнении развертки методом раскатки точки А2 , В2, С2 перемещаются по пер-

пендикулярам к боковым ребрам призмы. А натуральные величины отрезков СВ, ВА, АС

берутся из горизонтальной проекции, т.к. основание призмы параллельно плоскости П1. Бо-

67

ковые ребра остаются на развертке параллельными, т.к. каждая грань призмы является па-

Способ нормального сечения используется также для построения разверток приз-

вой поверхности призмы, строим пе-

риметр треугольника нормального се-

чения (рисунок 10.3б). Через точки сечения 1,2,3,1 проводим боковые ре-

бра перпендикулярно сечению и от-

кладываем на них натуральную вели-

чину, которая берется из фронтальной проекции рисунка 10.3а.

Соединив построенные точки,

получим развертку боковой поверх-

ности данной призмы (рисунок 10.3б).

Рисунок 10.3б

Построение приближенной развертки неразвертываемых поверхностей

Когда надо развернуть неразвертывающуюся поверхность ее заменяют развертыва-

ющейся (цилиндрической, конической, од-

ной или несколькими), имеющей общие линии с данной.

Такая замена называется аппрокси-

мацией, а полученная развертка – условной или приближенной.

Рассмотрим построение такой раз-

вертки на примере полусферы (рисунок

10.4).

69