posobie_TU

де w2 – частинне розв’язання неоднорідного рівняння, залежить від правої частини (виду розподіленого навантаження, прикладеного до пластинки).

Постійні інтегрування А1, А2, А3, А4 визначаються з граничних умов на зовнішньому і внутрішньому контурі пластини для кожної конкретної задачі (дві умови на кожному контурі).

б) позитивні моменти і поперечні сили указані на рис. 2.4.

40

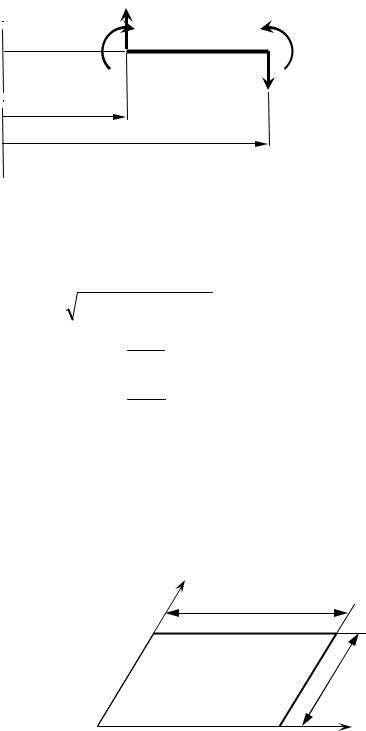
M>0, Q>0

rB

rЗ

Задача 2.1. Визначити умови на контурі для прямокутної пластини, яка

зображена на рис. 2.5, якщо функція прогину серединної поверхні має вигляд w C x a y b x 2a y 2b .

y

a

A B

b

O C

x

Рис. 2.5

Рішення. Знайдемо похідні (про умови закріплення можна судити по першим похідним, які відповідають кутам повороту):

ВС: x=a, w(a, y) 0 ,

w(a, y) C( y 2b)( y b)(2a 3a) 0 - шарнір.

x

ОС: y=0, w(x,0) 2Cb2 (x a)(x 2a) 0 ,

w(x,0) C(x a)(x 2a)(2 0 3b) 0 - вільна грань.

y

AB: y=b, w(x,b) 0 , w(x,b) C(x a)(x 2a)(2b 3b) 0 - шарнір.

y

Відповідь: ОА – вільна грань, ВС – шарнір, ОС – вільна грань, AB – шарнір.

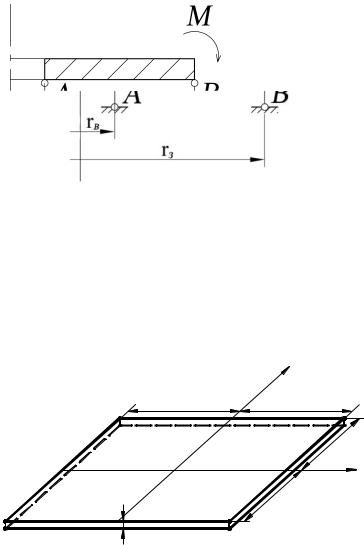
Задача 2.2. Записати умови на контурі кільцевої пластинки, що зображена на рис. 2.6, для визначення постійних інтегрування.

Рис. 2.6

Відповідь: Внутрішній контур: w=0, Mr=0. Зовнішній контур: w=0, Mr=-M.

b

x

42

Рішення. Знайдемо похідні для визначення граничних умов:

Відповідь: ОА – вільна грань, ВС – вільна грань, ОС – шарнір, AB – шарнір.

2.2.2 Задачі для самостійної роботи

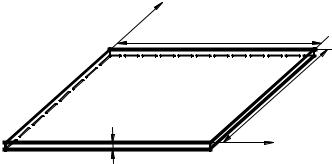
Задача C.2.1. Записати умови на контурі для кільцевої пластини, яка зображена на рис. 2.8.

Рис. 2.8

Задача C.2.2. Визначити умови на контурі для прямокутної пластини, яка зображена на рис. 2.5, якщо функція прогину серединної поверхні має вигляд:

w Cxy(x 2a)( y b) .

Задача C.2.3. Визначити умови на контурі для прямокутної пластини, яка зображена на рис. 2.7, якщо функція прогину серединної поверхні має вигляд:

43

2.3 Розрахункова робота №2 «Згин тонких пластинок. Прямокутні пластинки»

2.3.1 Зміст роботи

Прямокутна пластина з розмірами a×b, або 2a×2b у плані згинається під дією поперечного навантаження q. Рівняння пружної поверхні пластинки w задане.

Потрібно:

1.Побудувати епюри згинальних моментів і поперечних сил в перерізах x

або у.

2.Визначити найбільші нормальні і дотичні напруження.

Вихідні дані прийняти за варіантом у Додатку Г.

2.3.2Порядок виконання роботи

1.Встановити, яким граничним умовам пластини відповідає запропоноване рівняння серединної поверхні w(x, у).

2.Визначити постійний коефіцієнт C, що входить в рівняння зігнутої серединної поверхні пластинки.

3.Скласти вирази згинальних і крутильного моментів та поперечних

сил.

4.Побудувати епюри згинальних і крутильного моментів та поперечних сил в перерізах x або у.

5.Визначити найбільші нормальні і дотичні напруження.

2.3.3Приклад 1 виконання розрахункової роботи №2

Вихідні дані: прямокутна пластинка розмірами a×b, згинається під дією поперечного навантаження q (рис. 2.9). Рівняння пружної поверхні задане в поліномах.

Потрібно:

1.Побудувати епюри моментів і поперечних сил в перерізі x=a/3.

2.Визначити найбільші нормальні і дотичні напруження.

Рішення

1. Встановимо граничні умови і характер закріплення пластинки. Визначаємо похідні 1-го порядку для заданої функції прогину пластинки:

44

w Cy(x a)( y b) Cxy( y b) Cy( y b)(2x a) ,

x

w Cx(x a)( y b) Cxy(x a) Cx(x a)(2 y b) .

y

Визначимо характер закріплення граней пластинки:

Грань OA: x = 0, w(0,y)= C·0·y(0-a)(y-b)=0,

w(0, y) Cy( y b)(2 0 a) Cya( y b) 0 - шарнір.

x

Грань ВС: x = a, w(a,y)=C·a·y(a-a)(y-b)=0,

w(a, y) Cy( y b)(2 a a) Cya( y b) 0 - шарнір.

x

Грань ОС: y=0, w(x,0)=C·x·0(x-a)(0-b)=0,

w(x,0) Cx(x a)(2 0 b) bCx(x a) 0 - шарнір.

y

Грань AB: y = b, w(x,b)=C·x·b(x-a)(b-b)=0,

w(x,b) Cx(x a)(2 b b) bCx(x a)b 0 - шарнір.

y

Отже, всі грані пластини шарнірні (рис. 2.10).

y

a

A B

b

O C

x

Рис. 2.10

2. Визначимо коефіцієнт C, використовуючи диференціальне рівняння пружної поверхні пластинки (2.1). Для цього знайдемо похідні, які входять до рівняння Софі Жермен - Лагранжа (2.1):

4 w 0; 4 w 0.

x4 y4

Підставивши знайдені значення в рівняння (2.1), отримаємо:

2 4C Dq : C 8qD .

45

3. Складемо вирази згинальних моментів Mx, My, крутильного моменту Mxy та поперечних сил Qx, Qy, враховуючи:

При x=а/3 отримані формули спрощуються і мають вигляд:

Використовуючи отримані формули, обчислюємо значення цих силових чинників в перерізі x =1 м. Розділимо переріз пластини на 10 ділянок по 0,2 метра (11 точок).

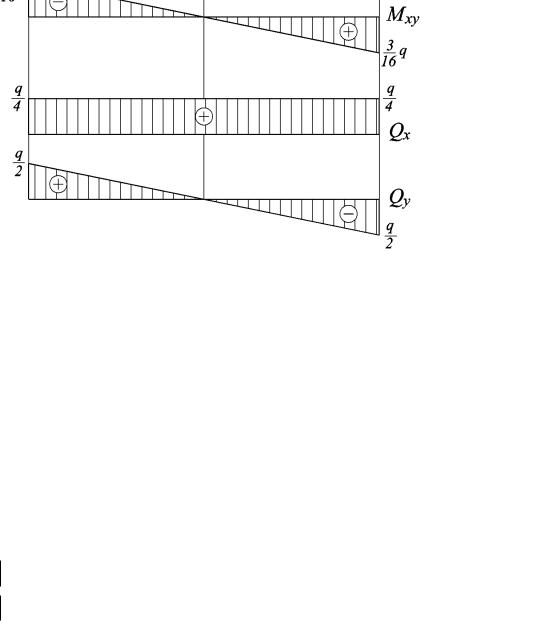
Результати розрахунків зведемо в таблицю 2.1. Таблиця 2.1 (початок) – Внутрішні зусилля в пластині

46

Таблиця 2.1 (закінчення) – Внутрішні зусилля в пластині

Відповідні епюри з інтервалом 0,2 м показані на рис. 2.12.

Визначаємо найбільше нормальне і дотичне напруження. Для цього спочатку визначимо геометричні характеристики полоси шириною b1 = 1 м, вирізаної з пластини паралельно осі x або паралельно осі у.

h x,y

Рис. 2.11

Момент опору прямокутного перерізу товщиною h і шириною b1 =1 м відносно осей x та y:

Статичний момент відносно осей x та y відсіченої площі прямокутного перерізу товщиною h/2 і шириною b1 = 1 м:

Осьовий момент інерції прямокутного перерізу відносно осей x та y товщиною h і шириною b1 =1 м:

47

Дотичні напруження:

2.3.4 Приклад 2 виконання розрахункової роботи №2

Вихідні дані: прямокутна пластинка розмірами 2a×2b, згинається поперечним навантаженням q (рис. 2.13). Рівняння пружної поверхні задане.

48

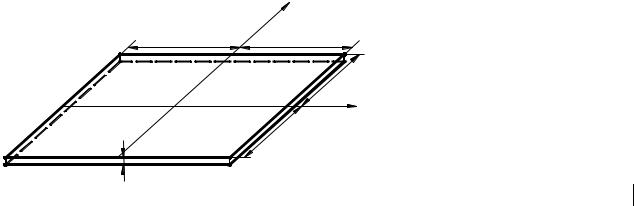
Потрібно:

1.Побудувати епюри моментів і поперечних сил в заданому перерізі.

2.Визначити найбільші нормальні і дотичні напруження.

Рис. 2.13

Рішення

1. Встановимо граничні умови на контурі пластинки. Для цього визначимо похідні 1-го порядку для заданої функції прогину пластинки:

49