posobie_TU

– міцність за максимальними дотичними напруженнями:

Міцність балки за максимальними нормальними і дотичними напруженнями забезпечена.

1.4Питання до тестового контролю за навчальним модулем №1

1.1.Основа, яка деформується під дією навантаження на балку, надаючи при цьому протидію прогину балки, називається:

А) пружною; Б) суцільною; В) жорсткою;

Г) нескінченною.

1.2.Балкою на пружній основі можна назвати:

А) ригель рами будівлі; Б) стрічковий фундамент; В) залізничну рейку; Г) підкранову балку.

1.3.Визначивши для балки на пружній основі суму проекцій всіх зовнішніх сил на вісь у, ми отримаємо:

А) опорну реакцію на лівій опорі балки; Б) сумарну реакцію з боку основи на балку;

В) рівнодіючу проекцій всіх зовнішніх сил на балку; Г) суму зосереджених сил, що діють на балку.

1.4.Коефіцієнт жорсткості основи – це:

А) реакція основи на площі 1 м2 при прогині основи, що дорівнює 1 м; Б) сумарна реакція основи при дії зосередженої сили, яка дорівнює;

В) опорна реакція на лівому краю балки від дії зосередженої сили, рівній одиниці;

Г) щільність основи.

1.5.Балки на пружній основі за методом розрахунку класифікуються як: А) нескінченно довгі і короткі; Б) довгі, короткі, нескінченно короткі; В) великі і малі; Г) високі і низькі.

1.6.Метод початкових параметрів рекомендується для розрахунку:

А) коротких балок; Б) нескінченно довгих балок;

В) абсолютно жорстких балок; Г) нескінченно коротких балок.

30

1.7.При розрахунку балок на пружній основі застосовуються функції: А) Крилова; Б) Вінклера; В) Гука; Г) Ньютона.

1.8.Кількість ділянок, на які розбивається балка, залежить від:

А) кількості зовнішніх навантажень на балку; Б) матеріалу балки; В) коефіцієнта податливості основи; Г) довжини балки.

1.9.Початкові параметри (для методу початкових параметрів) при розрахунку балок на пружній основі визначаються:

А) на підставі умов закріплення балки; Б) виходячи з довжини балки; В) виходячи з величин опорних реакцій;

Г) виходячи з величини прикладеного розподіленого навантаження.

1.10.Величиною «L» називається:

А) довжина балки; Б) безрозмірний коефіцієнт;

В) висота перерізу балки; Г) параметр, що визначає тип балки і що має розмірність довжини.

1.11.Жорсткість основи приймається залежно від: А) умов закріплення балки; Б) навантаження на балку; В) матеріалу балки; Г) составу основи.

1.12.Постійні інтегрування залежать від:

А) умов закріплення і навантаження на балку; Б) розрахункового опору матеріалу балки; В) матеріалу балки і основи; Г) матеріалу основи.

1.13. Безрозмірний коефіцієнт ξ визначається за формулою:

31

1.14.При розрахунку короткої балки на епюрі згинальних моментів під точкою прикладення зосередженого моменту:

А) спостерігається стрибок, значення якого дорівнює значенню моменту; Б) нічого не спостерігається; В) спостерігається перегин; Г) момент дорівнює нулю.

1.15.Позначення v0, φ0, M0, Q0 – це:

А) початкові параметри; Б) умовні позначення епюр;

В) позначення зовнішніх навантажень на балку; Г) внутрішні зусилля, що діють в балці.

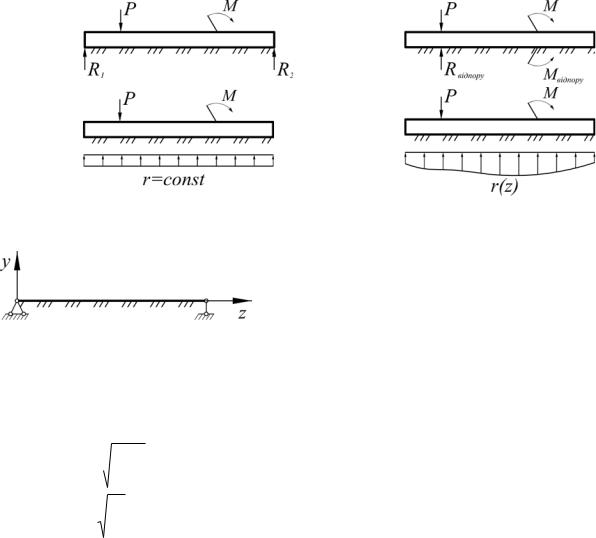
1.16. Схема, яка найточніше відображає роботу балки на пружній основі за гіпотезою Вінклера:

1.17. Для заданої балки правильними початковими параметрами будуть:

А) v0≠0, φ0≠0, M0≠0, Q0≠0; Б) v0=0, φ0≠0, M0=0, Q0≠0; В) v0=0, φ0≠0, M0≠0, Q0≠0; Г) v0≠0, φ0=0, M0≠0, Q0=0.

1.18. Параметр L обчислюється за формулою:

32

1.19.Значення згинального моменту, що виникає в балці на пружній основі, залежить:

А) тільки від прикладеного навантаження; Б) тільки від прикладеного навантаження і характеристик основи; В) тільки від характеристик матеріалу балки;

Г) від прикладеного навантаження, характеристик матеріалу балки і основи;

Д) від характеристик матеріалу балки і характеристик основи.

1.20.Приналежність балок на пружній основі до нескінченно довгих або коротких балок визначається на підставі:

А) виду навантажень, що діють на балку; Б) значень навантажень, що діють на балку; В) характеристик балки і основи; Г) умов закріплення балки.

1.21.Для балки на пружній основі за гіпотезою Вінклера реакція основи на одиницю довжини балки визначається:

А) за формулою r( z) k v( z) ; Б) тільки дослідним шляхом; В) за формулою r( z) Q0 ;

Г) за формулою r( z) q L .

1.5 Контрольна робота за навчальним модулем №1

1.5.1 Зміст роботи

Коротка балка прямокутного перерізу, розмірами bxh лежить на суцільній пружній основі. Необхідно:

1.Визначити початкові параметри для даної балки, прийнявши початок координат на лівому краю балки.

2.Записати рівняння для визначення v(z), φ(z), M(z) і Q(z) для перерізу, розташованого нескінченно близько праворуч від межі між першою і другою ділянкою.

1.5.2. Приклад виконання роботи

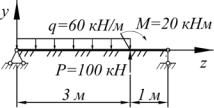
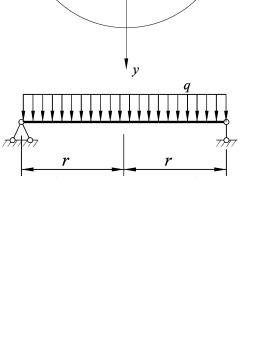
Вихідні дані: балка розмірами b=20см, h=30 см. Модуль пружності матеріалу балки E=3·104 МПа. Основа – пісок середньої крупності з коефіцієнтом жорсткості основи k=20 МПа. Розрахункова схема на рис. 1.16.

Рис. 1.16

33

Рішення

Приймемо початок координат на лівому кінці балки. Відповідно до умов закріплення маємо, що при z=0 (а) v=0, (b) M=0; при z=l=4 м (с) v=0, (d) M=0. З перших двох граничних умов (а) і (b) витікає, що початкові параметри v0=0, M0=0. Для визначення початкових параметрів Q0 і φ0 складаємо рівняння (1.21), (1.23) на підставі двох останніх граничних умов (с) і (d):

Визначимо значення функцій Крилова для z=0, z=3 м і z=4 м. Результати зводимо до табл. 1.10.

Вирішивши отриману систему, знайдемо початкові параметри

Q0=49,543 кН, φ0=-1,7742·10-3 рад.

Використовуючи рівняння (1.21)-(1.24), запишемо вирази для визначення v(z), φ(z), M(z) і Q(z) для указаного перерізу, розташованого на відстані 3 м від початку координат:

Відповідь: Q0=49,543 кН, φ0= -1,7742·10-3 рад.

34

Навчальний модуль 2. Розрахунки круглих та прямокутних пластин

2.1Стислі теоретичні відомості

2.1.1Основні поняття та залежності. Прямокутні пластинки

Прямокутною пластинкою називається пружне тіло призматичної форми з малою, в порівнянні з розмірами основи, товщиною h. Співвідношення

товщини пластинки до найменшого розміру в плані складає 801 15 , величина

очікуваних прогинів знаходиться в проміжку 14 h 12 h .

Площина, що ділить пластинку навпіл по товщині, називається серединною поверхнею. При згині пластинки серединна поверхня перетворюється на зігнуту серединну поверхню пластинки. Лінія перерізу бокової поверхні з серединною поверхнею називається контуром пластинки.

Теорія пластинок ґрунтується на ряду гіпотез:

1.Гіпотеза про нерозтяжність серединної поверхні;

2.Гіпотеза відсутності тиску між шарами пластини;

3.Гіпотеза прямих нормалей – будь-який лінійний елемент, нормальний до серединної поверхні пластинки, залишається таким і після її деформації.

Ці гіпотези дозволяють звести тримірну задачу до двомірної і прийняти,

що в пружній стадії роботи напруження σx, σy, τxy змінюються по товщині пластинки по лінійному закону. Отже, замість напружень, що діють в перерізах пластинки, можна розглядати зусилля і моменти (рис. 2.1), що їх замінюють.

Для дослідження деформацій пластинки, прямокутну систему координат прийнято розташовувати так, щоб координатна площина xOy співпала з серединною поверхнею пластинки, а вісь z направлена вниз. Тоді переміщення, що становить w у напрямі осі z, буде прогином пластинки.

Розв’язання задачі про згин пластинки зводиться до знаходження рівняння прогину w(x,y) (тобто рівняння пружної поверхні пластинки), яке задовольняло

босновному рівнянню згину пластинки (диференціальне рівняння пружної поверхні пластинки, яке називають зазвичай рівнянням Софі ЖерменЛагранжа) і умовам на опорному контурі (граничним умовам).

Диференціальне рівняння пружної поверхні пластинки записується так:

де q(x,y) – інтенсивність поперечного навантаження на пластинку; D – циліндрична жорсткість пластинки.

35

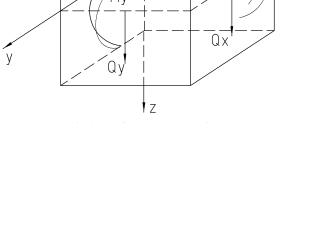
Рис. 2.1. Внутрішні зусилля в елементі пластинки:

Mxy= Myx – крутильні моменти, Mx, My – згинальні моменти відносно осей x та y відповідно, Qx, Qy – поперечні сили відносно осей x та y відповідно.

Рівняння (2.1) є бігармонічним рівнянням четвертого порядку в частинних похідних з правою частиною.

Після знаходження з (2.1) рівняння прогинів, визначаються Mx, My – згинальні моменти відносно осей x та y відповідно, Mxy – крутильний момент, Qx, Qy - поперечні сили відносно осей x та y відповідно. Далі знаходимо напруження. Для чого є наступні залежності:

згинальні моменти:

де W – момент опору перерізу товщиною h і шириною b1 =1 м відносно осей x та y, I – момент інерції перерізу товщиною h і шириною b1 =1 м відносно осей x та y (переріз полоси, яка вирізається з пластини (рис 2.11).

Напруження σx, σy, τxy змінюються по висоті перерізу прямо пропорційно величині z. Дотичні напруження τzx і τzy, що паралельні осі z, змінюються по висоті перерізу згідно параболічного закону.

На контурі прийнято розрізняти наступні умови:

геометричні – задаються переміщеннями, тобто прогинами і кутами повороту серединної площини;

статичні – задаються зусиллями, одночасно переміщеннями та зусиллями. На кожному краю пластинки можна задати дві граничні умови, які

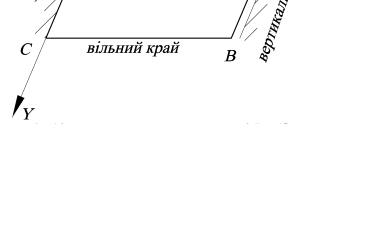
визначаються характером їх закріплення (рис. 2.2).

Рис. 2.2. Граничні умови по краях пластинки

Шарнірний край ОА: прогини дорівнюють нулю, а згинальні моменти дорівнюють нулю або задані, тобто w=0 і My=0 або f(x), отже, при y=0 і при будь-якому x. Якщо момент відсутній на контурі граничні умови мають вигляд:

Вільний край CB: згинальний момент My, поперечна сила Qy і крутильний момент Mxy дорівнюють нулю або задані. Останні дві умови можна об'єднати. В такому випадку для вільного краю записуються наступні умови (якщо на контурі відсутні поперечна сила, згинальний і крутильний моменти):

37

Умовні позначення:

Вільна грань. Прогин w 0 , кут повороту у відповідному напрямі wx 0 або wy 0 . Шарнірна грань. Прогин w 0 , кут повороту у відповідному напрямі wx 0 або wy 0 .

Затиснення. Прогин w 0 , кут повороту у відповідному напрямі wx 0 або wy 0 .

Вертикальний повзун Прогин w 0 , кут повороту у відповідному напрямі wx 0 або wy 0 .

Для прямокутної пластинки розв’язання основного диференціального рівняння в замкнутій формі отримати не вдається, тому доводиться його знаходити за допомогою різних наближених методів: методу рядів, методу кінцевих різниць (сіток), варіаційного методу Бубнова–Галеркина та ін. Деякі з них вимагають призначення апроксимуючої функції прогину.

В зв'язку з цим представляє інтерес розв’язання і таких задач, в яких задається вираз прогинів (рівняння пружної поверхні пластинки). В цьому випадку необхідно встановити, яким граничним умовам задовольняє задане рівняння, скласти вирази моментів і поперечних сил, а також визначити значення найбільшого напруження.

При розв’язанні задач рекомендується наступний план рішення:

1.Встановити, яким граничним умовам відповідає задане рівняння пружної поверхні w(x, у).

2.Визначити постійний коефіцієнт, що входить в рівняння зігнутої серединної поверхні пластинки.

3.Скласти вирази моментів і поперечних сил.

4.Побудувати епюри моментів і поперечних сил в перерізах x або у.

5.Визначити найбільші нормальні і дотичні напруження.

2.1.2 Основні поняття та залежності. Кільцеві пластинки

Для розрахунку кільцевих пластин отримані раніше рівняння, які були виведені для декартової системи координат, перетворимо в рівняння для полярної системи координат.

38

Розрахунком круглих і кільцевих пластинок, що знаходяться під дією навантажень, симетричних щодо полюса, є розв’язання одновимірної задачі. Функція прогину серединної поверхні в цьому випадку залежить від радіусу r і не залежить від полярного кута θ, тобто w(r, ) w(r) .

Рис. 2.3 Розрахункова схема круглої пластинки

У формулах (2.12) – (2.26) прийнято:

Mr – радіальний згинальний момент в перерізі, перпендикулярному радіусу вектору r в даній точці;

Mθ – тангенціальний (кільцевий) згинальний момент в перерізі, паралельному радіусу r в даній точці.

Qr – радіальна поперечна сила на площині з нормаллю r.

Qθ – тангенціальна (кільцева) поперечна сила на площині, яка співпадає з

радіусом r.

В цьому випадку диференційне рівняння згину пластинки в полярній системі координат:

В цьому випадку можна розглядати половину перерізу пластини. Формули внутрішніх силових чинників:

39