Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Донбасская национальная академия строительства и архитектуры

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

КЛ по Информатике-2008-часть2_укр

.pdf

Скачиваний:

Добавлен:

21.02.2016

Размер:

4 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 117 8 9 10 11 > Следующая >>>

L	(x)=	(x − x0 ) (x − x1 ) ... (x − xi−1 ) (x − xi+1 ) ... (x − xn )	(2.34)
L	(x)=	(xi − x0 ) (xi − x1 ) ... (xi − xi−1 ) (xi − xi+1 ) ... (xi − xn )	(2.34)
i

Багаточлени (2.34) називаються коефіцієнтами Лагранжа.
Багаточлен Pn (x), що вирішує задачу алгебраїчної інтерполяції, може бути представ-
лено у вигляді:		n
		n
Pn (x)= y0 L0 (x)+ y1 L1 (x)+ ...+ yn Ln (x)= ∑yi Li (x)			(2.35)
		i=0
Для вузла x = xi згідно умовам (2.32) зі всієї суми у формулі (2.35) залишається один

доданокPn (xi )= yi Li	(xi	), а оскількиLi (xi )= 1 , то це означає виконання умов інтерполяції
(2.31).
Багаточлен	(x − x0 ) (x − x1 ) ... (x − xi−1 ) (x − xi+1 ) ... (x − xn )
n
Pn (x)= ∑yi			(2.36)
Pn (x)= ∑yi	(xi	− x0 ) (xi − x1 ) ... (xi − xi−1 ) (xi − xi+1 ) ... (xi − xn )	(2.36)
i=0	(xi

називається інтерполяційним багаточленом Лагранжа.

2.3. Лінійна інтерполяція

В окремому випадку n = 1 (інтерполяція по двох вузлах) формула Лагранжа представляє рівняння прямої y = P1 (x), що проходить через дві задані точки (лінійна інтерполяція

(2.20)).

Лінійна інтерполяція (2.20)

Окрема задачі інтерполяції. Інтерполяція з використанням формули Лагранжа відбувається по двох вузлах

y = P	(x)=	x − x1	y	+	x − x0	y	1

1		x0 − x1	0		x1 − x0

2.4. Квадратична інтерполяція
При n = 2 (інтерполяція по трьох вузлах)				одержимо рівняння параболи y = P2 (x),

що проходить через три задані точки (квадратична інтерполяція (2.21)):

Квадратична інтерполяція (2.21)

Окрема задачі інтерполяції. Інтерполяція з використанням формули Лагранжа відбувається по трьох вузлах


y = P	(x)=	(x − x1 ) (x − x2 )	y +	(x − x0 ) (x − x2 )	y		+	(x − x0 ) (x − x1 )	y
y = P	(x)=	(x0 − x1 ) (x0 − x2 )	y +	(x1 − x0 ) (x1 − x2 )	y		+	(x2 − x0 ) (x2 − x1 )	y
2		(x0 − x1 ) (x0 − x2 )	0	(x1 − x0 ) (x1 − x2 )		1		(x2 − x0 ) (x2 − x1 )		2

Поліноми Лагранжа дають хорошу якість інтерполяції при великій кількості вузлів і високого ступеня полінома. До недоліків поліномів Лагранжа можна віднести те, що існують функції, при інтерполяції яких, збільшення ступеня полінома не дає хорошого наближення.

2.5. Обчислення інтерполяційного багаточлена Лагранжа в проміжних точках

Нехай необхідно обчислити Pn (x) в точці, що не співпадає з вузлами інтерполяції. Помножимо чисельник і знаменник у формулі (2.36) на x − xi ≠ 0 і введемо позна-

чення:

E (x )= (x − x0 ) (x − x1 ) ... (x − xi−1 ) (x − xi ) (x − xi+1 ) ... (x − xn )

Di (x )= (xi − x0 ) (xi − x1 ) ... (xi − xi−1 ) (x − xi ) (xi − xi+1 ) ... (xi − xn )

Тоді вираз

Pn (x )

= E (x ) ∑

)

(2.37)

i=0

Di (x

представлятиме значення полінома Лагранжа в крапці x = x .

Обчислення доцільно оформити у вигляді наступної таблиці:

Різниці

Di (x )

)

Di (x

x − x0

x0 − x1

x0 − x2

…

x0 − xn

x1 − x0

x − x1

x1 − x2

…

x1 − xn

x2 − x0

x2 − x1

x − x2

…

x2 − xn

…

n xn − x0

xn − x1

xn − x2

…

x − xn

E (x )=

S =

У стовбці Di (x ) записується добуток елементів відповідного рядка таблиці різ-

ниць, а величина E (x ) обчислюється як добуток підкреслених елементів головної діаго-

налі таблиці різниць. Обчисливши E (x ) і суму S елементів останнього стовпця розраху-

нкової таблиці знаходимо значення багаточлену Лагранжа в точці x = x як добуток цих величин.

2.6. Реалізація метода інтерполяції в MS Excel

Приклад реалізації задачі інтерполяції в Microsoft Excel наведено на рис. 2.6.

§ 3. Методи обробки даних: метод найменших квадратів

3.1. Постановка задачі

Визначення виду функціональних залежностей, що одержано у фізичному експерименті, має дуже важливе значення. Так, у результаті експериментів часто одержують сукупність

точок (x1 , y1 )...(xN , yN ), абсциси яких {xk } різні. Одне із призначень чисельних методів – визначення формули виду y = f (x), що пов’язує ці змінні, точніше – вибір класу припустимих формул, коефіцієнти в яких повинні бути визначені.

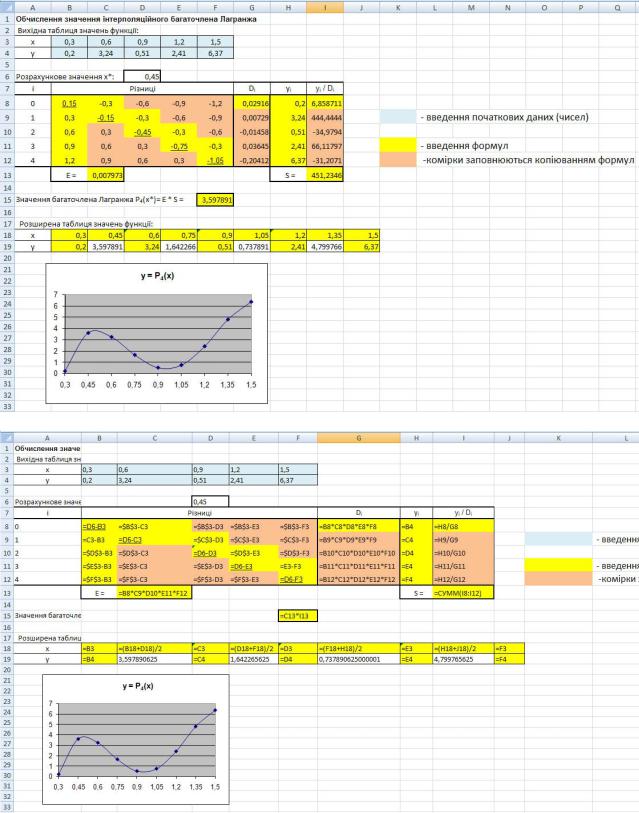
а)

б)

Рис. 2.6. Приклад реалізації задачі інтерполяції в Microsoft Excel: а) вид листа Microsoft Excel; б) формули, що розташовано в комірках листа Microsoft Excel

Якщо всі чисельні значення {xk }, {yk } відомі з декількома знаками точності, то інте-

рполяційний поліном може бути з успіхом використаний, інакше це неможливо. У деяких експериментах застосовується спеціалізоване устаткування, що дозволяє одержати вимірювані точки, принаймні, з п’ятьма знаками точності. Однак більшість експериментів проводиться на устаткуванні, що надійно дає тільки три або менше знаки точності. Часто у вимірі

присутнє експериментальна помилка. І хоча записуються три цифри для значень {xk }, {yk }

мається на увазі, що справжнє значення f (xk ) задовольняє рівності:
f (xk )= yk +εk	(2.38)

де εk – помилка виміру.

Для визначення кращого наближення функції до отриманих точок, проведемо дослі-

дження помилок (які також можна називати відхиленнями або залишками):
εk = f (xk )− yk , для 1 ≤ k ≤ N .	(2.39)

Існує декілька норм (2.22), які можна використати із залишками в (2.39), щоб виміряти, наскільки далеко від даних лежить крива y = f (x).

Норма (2.22)

Норма (від лат. norma — керівний початок, правило, зразок) – встановлена міра, середня величина чого-небудь.

Максимальна помилка:

E∞ ( f )= max {

f (xk )− yk

}

(2.40)

1≤k≤N

Середня помилка:

( f )=

∑

f (xk )− yk

(2.41)

k =1

1 2

f (xk )− yk

Середньоквадратична помилка:

( f )=

∑

(2.42)

k =1

Розглянемо це на прикладі.

Приклад.

Порівняти максимальну, середню і середньоквадратичну помилки для лінійного на-

ближення	функції		y = f (x)= 8,6 −1,6 x				по заданих		крапках			(−1;10), (0;9), (1;7 ),
(2;5), (3;4), (4; 3), (5;0)				і (6;−1).
			12
			12
			10


			8


			6


													Yk
													Yk
			4										f(xk)=8,6 1,6*xk
													f(xk)=8,6 1,6*xk

			2


			0


	2	1	0	1	2	3	4	5		6	7
			2
			2
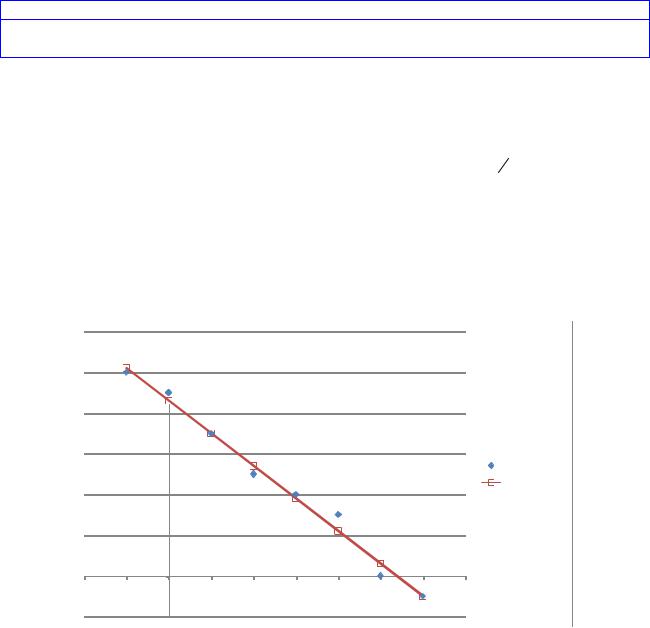
Рис. 2.7.		Графік функції y = f (x)= 8,6 −1,6 x з нанесеними крапками

Знайдемопомилки, використовуючизначенняфункції f (xk ) і εk , отриманівтаблиці2.4.

				Обчислення для знаходження E1 ( f )				і E2 ( f )		Таблиця 2.4
				Обчислення для знаходження E1 ( f )				і E2 ( f )
xk				yk		f (xk )= 8,6 −1,6 xk			εk	εk2
xk				yk		f (xk )= 8,6 −1,6 xk			εk	εk2
								0,2
-1				10		10,2		0,2		0,04
0				9		8,6		0,4		0,16
1				7		7,0		0,0		0,00
2				5		5,4		0,4		0,16
3				4		3,8		0,2		0,04
4				3		2,2		0,8		0,64
5				0		0,6		0,6		0,36
6				-1		-1,0		0,0		0,00
						∑		2,6		1,40
							0,8
E∞ ( f )= max{0,2;0,4;0,0;0,4;0,2;0,8;0,6;0,0}=							0,8
E1	( f )=	1	(2,6)= 0,325
		8
E2			1,4	1 2	≈ 0,41833
E2	( f )=				≈ 0,41833
			8

Зрозуміло, що максимальна помилка найбільша і якщо одна крапка погана, те її значення визначає E∞ ( f ). Середня помилка E1 ( f ) – просто середнє абсолютних величин помилок різних крапок. Вона часто використовується завдяки простоті обчислення. Помилку E2 ( f ) часто використають при вивченні помилок статистичної природи.

Найкраща побудована лінія визначається шляхом мінімізації однієї з величин, заданих виразами (2.40) – (2.42). Таким чином, можна знайти три лінії, побудовані щонайкращим об-

разом. Традиційно обирається третя норма E2 ( f ) тому, що її набагато легше мінімізувати.

3.2. Метод найменших квадратів

Нехай залежність між змінними x та y представлена таблицею даних, отриманих в експерименті:

X	x1	x2	…	xN
Y	y1	y2	…	yN

Потрібно отримані дані описати деякою функціональною залежністю вигляду y = f (x). Така залежність повинна відбити основну тенденцію зміни змінної y зі зміною

змінної x і згладити випадкові погрішності вимірів, які є неминучими в експерименті. Задача знаходження емпіричної формули (2.23) складається із двох основних етапів.

Емпірична формула (2.23)

Формула, що служить для аналітичного подання дослідних даних.

Напершомуетапі необхідно встановитивиглядзалежності y = f (x), тобтовирішитичиє вона лінійною f (x)= a0 + a1 x , квадратичною f (x)=a0 +a1 x+a2 x2 , логарифмічною f (x)=a0 +a1 ln(x) або який-небудь іншою. Для цього експериментальні точки наносять на координатну площинуіпоїхрозташуваннювисуваютьгіпотезупровиглядемпіричноїзалежності.

На другому етапі, коли загальний вид емпіричної функції обрано, необхідно визначити числові значення її параметрів a0 , a1 , a2 ,..., an . Критерієм вибору значень параметрів є

метод найменших квадратів (МНК) (2.24).

Метод найменших квадратів (МНК) (2.24)

Метод найменших квадратів – один з методів теорії помилок для оцінки невідомих величин за результатами вимірів, що містить випадкові помилки. Застосовується при обробці спостережень.

У методі найменших квадратів апроксимація (2.25) відбувається на підставі того, що сума квадратів відхилень по всіх крапках повинна бути найменшою. Тобто:

Апроксимація (2.25)

Апроксимація (від лат. approximo — наближаюся), заміна одних математичних об’єктів (напр., чисел або функцій) іншими, простішими і в тому або іншому значенні близькими до вихідних (напр., кривих ліній близькими до них ламаними).

N	N	( f (xk )− yk )2 min ,
F = ∑δk	=∑	( f (xk )− yk )2 min ,	(2.43)
k =1	k=1
де δk – відхилення.
Якщо взяти поліном у вигляді:
f (x)=a0 +a1 x+a2 x2 +...+am xm ,			(2.44)

то F = F (a0 ,a1 ,...,am )

Помітно, що ступінь поліному m повинна бути менше числа крапок N . (У випадку m = N − 1 одержимо поліном Лагранжа).

3.3. Лінійна апроксимація

У цьому випадку m = 1 , тоді апроксимуюча функція буде мати вигляд:

f (x)=a0 +a1 x

(2.45)

Згідно МНК значення її параметрів підбираються таким чином, щоб відхилення експериментальних точок (xk ; yk ) від обраної кривої було мінімальним. Тобто параметри a0 ,

a1 повинні бути такими, щоб сума квадратів відхилень спостережуваних значень yk від роз-

рахованих за функцією (2.45), була мінімальною. Сума квадратів відхилень від лінійної функції (2.45) має вигляд:

			N
F (a0 , a1 )= ∑(a0 + a1 xk − yk )2 min							(2.46)
		k =1
ЗВЕРНІТЬ	Величина E2 ( f )			буде мінімальної тоді і тільки тоді, коли
ЗВЕРНІТЬ	Величина E2 ( f )			буде мінімальної тоді і тільки тоді, коли
УВАГУ!	буде мінімальної величина (2.46).
УВАГУ!
NB !

Величина F (ao ,a1 )		є функцією двох змінних. Необхідною умовою екстремуму такої
функції є рівність нулю всіх її окремих похідних:
		∂F (ao ,a1 )	= 0		∂F (ao ,a1 )	= 0	(2.47)
		∂a0	= 0		∂a1	= 0	(2.47)
		∂a0			∂a1

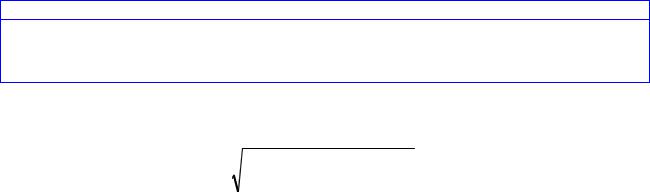
Вони мають вигляд:

∂F (a0 , a1 )	N	(a0 + a1 xk − yk )= 0
	= 2∑
∂a0
	k =1	(2.48)
∂F (a0 , a1 )	N
	= 2∑	(a0 + a1 xk − yk ) xk = 0
∂a1
	k =1

Таким чином, після перетворення маємо нормальну систему двох лінійних рівнянь щодо невідомих параметрів регресії a0 , a1 .

		N	N
a0 N + a1 ∑xk =			∑yk
		k =1	k =1	(2.49)
	N	N	N	(2.49)
a0 ∑xk + a1 ∑xk2 = ∑ yk xk
	k =1	k =1	k =1

Рішення системи – значення параметрів a0 , a1 можна знайти методом зворотної матриці. Представимо систему (2.49) у матричній формі:

∑N xk

k =1

Тоді:

∑xk

∑yk

k =1

= k =1

або

= B

∑xk2

∑ yk

k =1

= A−1

(2.50)

Знайдені параметри регресії a0 , a1 підставляють у рівняння (2.45) і в такий спосіб

одержують емпіричне лінійне рівняння, яке найкращим чином описує експериментальні дані. Для оцінки відповідності підібраної прямої і експериментальних даних уводять по-

няття коефіцієнта лінійної кореляції (2.26), що обчислюється за формулою:

Коефіцієнт лінійної кореляції (2.26)

Коефіцієнт кореляції характеризує тісноту лінійної залежності і приймає значення в інтервалі −1 ≤ Ryx ≤ 1 . Чим ближче Ryx до 1 або -1, тим тісніше лінійний зв’язок (прямий або зво-

ротній) між змінними х та у.

∑(xk −

) (yk −

)

Ryx =

k =1

(2.51)

∑(xk −

∑(yk −

k =1

k=1

де:

∑xk ,

∑yk – середні величини змінних х та у.

k =1

3.4. Квадратична апроксимація

Якщо m = 2 , то одержуємо функцію:

f (x)= a0 + a1 x + a2 x2

(2.52)

У цьому випадку нормальна система має вигляд:

∂F (a0 , a1 ,a2 )

(a0 + a1 xk + a2 xk 2 − yk )= 0

= 2∑

∂a0

k =1

∂F (a

, a

)

= 2∑(a0 + a1 xk + a2 xk

2 − yk ) xk = 0

(2.53)

∂a1

)

k =1

∂F (a

, a

(a0 + a1 xk + a2 xk 2 − yk ) xk 2 = 0

= 2∑

∂a

k =1

Після перетворення маємо нормальну систему трьох рівнянь щодо невідомих параметрів регресії a0 , a1 , a2 :

	N		N	N
a0 N + a1 ∑xk + a2 ∑xk2 =				∑ yk
	k =1		k =1	k =1
	N	N	N	N
a0	∑xk + a1	∑xk2 + a2 ∑xk3 = ∑xk yk			(2.54)
	k =1	k =1	k =1	k =1
	N	N	N	N
a0	∑xk2 + a1	∑xk3 + a2 ∑xk4 = ∑xk2 yk
	k =1	k =1	k=1	k =1
Розв’язавши систему (2.54) щодо параметрів a0 , a1 , a2					одержуємо конкретний вид

функції (2.52). Зміна кількості параметрів не призведе до зміни суті самого підходу, а виразиться в зміні кількості рівнянь у системі (2.54).

Значення різниць
yk − F (a0 ,a1 ,a2 )= εk	(2.55)

називають відхиленнями обмірюваних значень від обчислених за формулами (2.45) або

(2.52).

Сума квадратів відхилень

N
σ = ∑εk2		(2.56)
k =	1

відповідно до принципу найменших квадратів для заданого виду функції, що наближає, повинна бути найменшої.

ЗВЕРНІТЬ	Із двох різних наближень однієї й тієї ж табличної функції
УВАГУ!	кращим вважається те, для якого (2.56) має найменше зна-
NB !	чення.
NB !

Аналогічно можна записати систему для полінома будь-якого ступеня m ≤ N :

f (x)= a0 + a1 x + a2 x2 + ...+ am xm

(2.57)

При цьому, якщо m = N , то точкова середня квадратична апроксимація алгебраїчним багаточленом збігається з лагранжевою інтерполяцією. Таким чином, підвищення ступеню апроксимуючого полінома на певному кроці приведе до погіршення якості. Інший шлях підвищення якості апроксимації пов’язано з вибором замість алгебраїчних поліномів інших ортогональних поліномів, а також функцій виду:

y = a xb		y = a bx		y = a +	b
					x

	1		x	(2.58)
y =		y =		y = a lg x
	a x + b		a x + b

і інших, які легко лінеаризуються шляхом логарифмування або заміни змінних (табл. 2.5,

рис. 2.8).

Таблиця 2.5

Заміна змінної (змінних) для метода лінеаризації даних

Функція,

y = f (x)

Лінеаризована форма,

Заміна змінної (змінних) і

Y = A x + B

постійних

y =

+ B

y = A

+ B

X =

, Y = y

y =

y = −1 (x y)+

X = x y , Y = y , C =

−1

x +C

−B

D =

y =

= A x + B

X = x , Y =

A x + B

y =

= A

+ B

X =

, Y =

A x + B

y = A ln(x)+ B

X = ln(x), Y = y

y = C eA x

ln(y)= A x + ln(C )

X = x , Y = ln(y), C = eB

y = C xA

ln(y)= A ln(x)+ ln(C )

X = ln(x), Y = ln(y),

C = eB

y = (A x + B)−2

y−1 2 = A x + B

X = x , Y = y−1 2

y = C x e−D x

= −D x + ln(C )

, C = e

X = x , Y = ln

D = −A

y =

−1 = A x + ln(C )

X = x , Y = ln

−1

1 +C e

A x

C = eB и L – постійні, що повинні бути задані

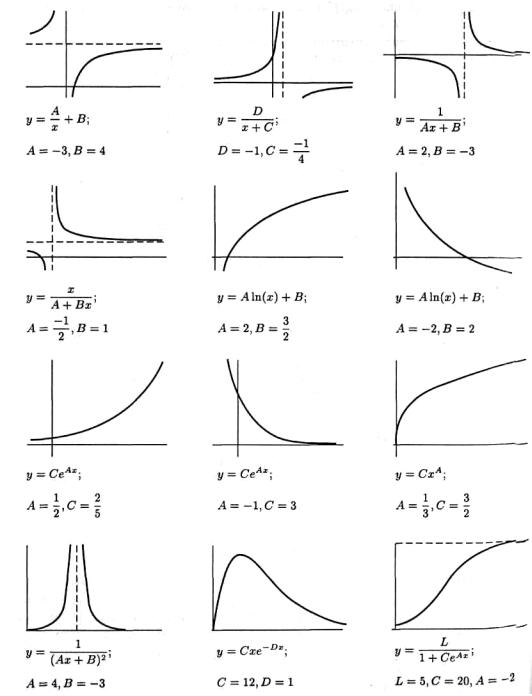
Рис. 2.8. Можливі криві, що використовують при лінеаризації даних

3.5. Реалізація метода найменших квадратів в MS Excel

Приклад реалізації методу найменших квадратів у середовищі Microsoft Excel наведено на рис. 2.9.

<<< < Предыдущая 1 2 3 4 5 67 / 117 8 9 10 11 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
21.02.20161.2 Mб10КЛ Осн. охорони праці.pdf
#
21.02.20164.73 Mб145КЛ по ВТиП-часть1.pdf
#
21.02.20164.73 Mб28КЛ по ВТиП-часть1_укр.pdf
#
21.02.20163.35 Mб195КЛ по ВТиП-часть2.pdf
#
21.02.20163.34 Mб40КЛ по ВТиП-часть2_укр.pdf
#
21.02.20164 Mб18КЛ по Информатике-2008-часть2_укр.pdf
#
09.11.201911.25 Mб46КЛ по технологии металлов.doc
#
21.02.20165.64 Mб39КЛ Спец констр МК.pdf
#
21.02.20166.99 Mб416КЛ. Материалы в мк.doc
#
21.02.20163.56 Mб29КЛ01Введение рус..pdf
#
21.02.2016268.74 Кб33Книга Виктора Гребенникова.docx