
КЛ по Информатике-2008-часть2_укр
.pdf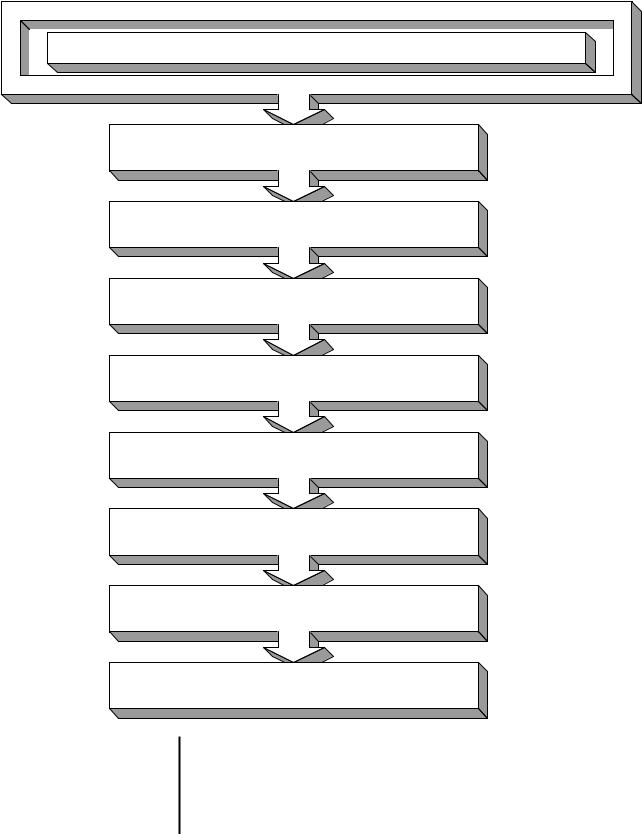
ЕТАПИ ДОСЛІДЖЕННЯ ПРИКЛАДНИХ ЗАДАЧ |
Фізична постановка задачі та її |
якісний анализ |
Пошук, вибір або модифікація |
математичної моделі |
Розробка, вибір або модифікація |
математичного методу |
Підготовка початкової інформації |
Укладання алгоритму |
Розробка програмного забезпечення |
Чисельне рішення |
Аналіз чисельних результатів та їх використання
Рис. 1.1 Основні етапи дослідження інженерних задач
ЗВЕРНІТЬ УВАГУ! NB !
Таким чином, можна помітити, що абсолютна погрішність – це проста різниця між істинним і наближеним значеннями, тоді як відносна погрішність – це частка істинного значення.
Оскільки величина а, як правило, невідома, а погрішність необхідно визначити, то в |
|||||
розгляд вводиться гранична абсолютна погрішність |
(a*): |
||||
a* = |
|
a − a* |
|
≤ (a*). |
(1.1) |
|
|
||||
Розкриваючи в цій нерівності модуль, одержуємо співвідношення, що задає відрізок, якому належить точне значення:
10

|
|
|
|
|
|
|
a * − |
(a*)≤ a ≤ a * + |
(a* ). |
(1.2) |
||||||||
Таким чином, величина а знаходиться в подвоєному |
-околі (дельта-околі), що ви- |
|||||||||||||||||
значається величинами а* і |
(a*) і складає відрізок [х1, х2] (рис. 1.2). |
|||||||||||||||||
|
|
|
|
|
|
x1 = a* − |
(a*) |
|
a* |
|
|
x2 = a* + (a*) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(a*) |
|
|
|
|
|
(a*) |
|
|
|
Рис. 1.2 Область визначення рішення |
|
|
|
|
|
|
|
|
|
|||||||||
Гранична |
відносна |
погрішність |
наближення а* |
визначається відношенням |
||||||||||||||
δ (a*)= |
|
|
(a*) |
. Звідси виходить часто використовуване співвідношення: |
||||||||||||||
|
|
a* |
|
|
||||||||||||||
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
(a*)=δ (a *) |
|
a * |
|
. |
(1.3) |
||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
1.3. Структура погрішності
Є чотири джерела погрішності результату: математична модель, початкові дані, наближений метод і округлення при обчисленнях (рис. 1.3).
СТРУКТУРА ПОГРІШНОСТІ РЕЗУЛЬТАТУ |
МАТЕМАТИЧНА МОДЕЛЬ |
|
ПОЧАТКОВІ ДАНІ |
|
ПОГРІШНІСТЬ МЕТОДУ |
|
ОКРУГЛЕННЯ ПРИ ОБЧИСЛЕННЯХ |
|
|
|
|
|
|
|
Рис. 1.3 Структура погрішності результату чисельного рішення
Один з типів погрішностей обумовлено неадекватністю обраної математичної моделі початковій фізичній. Ця неадекватність більшою чи меншою мірою властива всім приблизно вирішуваним задачам. Дана погрішність з’являється неусувною, і вона визначається на восьмому етапі рішення задачі (див. рис. 1.1). Решта трьох типів погрішностей є суто обчислювальними і обумовлені наступними причинами.
11

Початкові дані нерідко неточні; наприклад, це можуть бути експериментально зміряні величини. Так, наприклад, в високоточних фізичних вимірюваннях точність доходить до 10- 12, та вже характерна астрономічна і геодезична точність дорівнює 10-6, а в багатьох фізичних
ітехнічних задачах погрішність вимірювання буває 1 – 10%. Погрішність початкових даних
δx призводить до так званої неусувної (вона не залежить від математика) погрішності рі-
шення δ y = A(x +δ x)− A(x).
Якщо усунути невизначеність в початкових даних, наприклад, шляхом їх фіксації і знайти рішення за допомогою якого-небудь чисельного методу, то отримаємо результат, що не в точності відповідає початковим даним. Це є погрішність чисельного або якого-небудь іншого наближеного методу (наприклад, приблизно-аналітичного); саме такі погрішності оцінюватимуться при розгляді чисельних методів. Ці оцінки можуть бути отримані до виконання обчислень (оцінки апріорі (1.5)) і після них (оцінки апостеріорі (1.6)).
Апріорі (1.5)
АПРІОРІ (від лат. apriori – з передування), поняття логіки і теорії пізнання, що характеризує знання, передуюче досвіду і незалежне від нього; введено в середньовічній схоластиці в протилежність апостеріорі.
Апостеріорі (1.6)
АПОСТЕРІОРІ (від лат. aposteriori – з подальшого), що походить з досвіду; поняття теорії пізнання, протилежне апріорі.
Погрішність методу пов’язана з тим, що точні оператор і початкові дані замінюються наближеними. Наприклад, замінюють інтеграл сумою, похідну – різницею, функцію – багаточленом або будують нескінченний ітераційний процес і обривають його після кінцевого числа ітерацій. Методи будуються звичайно так, що в них входить деякий параметр; при прагненні параметра до певної межі погрішність методу прагне до нуля, так що цю погрішність можна регулювати.
Погрішність методу доцільно обирати так, щоб вона була в 2–5 разів менше за неусувну погрішність. Велика погрішність методу знижує точність відповіді, а помітно менша – невигідна, бо це звичайно вимагає значного збільшення об’єму обчислень.
Підрахунки, як на папері, так і на комп’ютері виконують із певним числом значущих цифр. Це вносить у відповідь погрішність округлення, яка накопичується в ході обчислень.
Відзначимо, що в більшості прикладних задач неприємностей можна уникнути, проводячи розрахунок із подвійною або потрійною точністю. Така можливість реалізована в хорошому математичному забезпеченні комп’ютерів; це у декілька разів збільшує час розрахунку, проте дозволяє користуватися вже відомими алгоритмами, а не розробляти нові.
При будь-яких розрахунках справедливе правило: треба утримувати стільки значущих цифр, щоб погрішність округлення була істотно менше за всю решту погрішностей.
1.4. Значущі цифри
Значущими цифрами наближеного числа називають всі цифри в його записі, починаючи із першої ненульової зліва.
Перші п значущих цифр наближеного числа називаються вірними, якщо абсолютна погрішність цього числа не перевищує половини одиниці розряду, відповідного п-ій значущій цифрі, вважаючи зліва направо. Зайві збережені цифри, крім вірних, називаються сумні-
вними.
Обчислити наближене число із точністю ε = 10−n означає, що необхідно зберегти вірною значущу цифру, що стоїть в п-м розряді після коми.
На практиці виникає необхідність в округленні наближеного числа, тобто заміні його числом із меншою кількістю значущих цифр. Для округлення числа до п значущих цифр слід відкинути всі його цифри, що стоять праворуч від п-ої значущої цифри. При цьому:
12
а) якщо перша із відкинутих цифр менше 5, то десяткові знаки, що залишилися, зберігаються без зміни;
б) якщо перша із відкинутих цифр більше 5 або рівна 5 і серед решти відкинутих цифр є ненульові, то до останньої цифри, що залишилася, додається одиниця;
в) якщо перша із відкинутих цифр рівна 5 і решта відкинутих цифр нульових, то остання цифра, що залишилася, не змінюється, якщо вона парна, і збільшується на одиницю, якщо вона непарна.
Абсолютна і відносна погрішності записуються у вигляді чисел із однією або двома значущими цифрами, і вони округляються з залишком. У записі наближених чисел їх запи-
сують таким чином: |
a = a* (1 ±δ ). |
|
|
|
a = a * ± |
(1.4) |
|
Наприклад, π = 3,141 ±0,0006 ; π = 3,141(1 ± 0,02%). |
|
||
Якщо |
в записі числа не вказано, то мається на увазі, що а має точність половини |
||
одиниці (1/2 од.) молодшого розряду. Так, для а=5,63 абсолютна погрішність |
= 0,005 . |
||
§ 2. Методи розв’язання нелінійних рівнянь: метод половинного ділення
2.1. Наближене розв’язання нелінійних рівнянь
Для досить складних алгебраїчних рівнянь (1.7) і трансцендентних рівнянь (1.8) не завжди можна знайти точне рішення, тому дуже часто доводиться застосовувати наближені (чисельні) методи знаходження коренів (1.9) таких рівнянь.
Алгебраїчне рівняння (1.7)
Рівняння називають алгебраїчним, якщо кожна з функцій, що входять до його складу є алгебраїчною (раціональною або ірраціональною). Одна з функцій може бути постійною ве-
личиною. Наприклад, x2 = 2
Трансцендентне рівняння (1.8)
Рівняння F (x)= f (x) називають трансцендентним, якщо хоча б одна з функцій F (x) або
f (x) не є алгебраїчною. Наприклад, 3x = 2 + 4x−2 ; |
x cos x = sin x |
|
|
Корінь (1.9) |
|
Коренем рівняння f (x)= 0 називається значення |
x = x* , що обертає функцію f (x) в |
нуль, тобто f (x* )≡ 0 . |
|
|
|
Нехай дано нелінійне рівняння |
|
f (x)= 0 |
(1.5) |
де f (x) – функція визначена і неперервна на якомусь (навіть нескінченному) інтервалі a < x < b . У деяких випадках на функцію f (x) можуть бути накладено додаткові обмеження, наприклад, неперервність першої і другої похідних, на що спеціально вказується.
Потрібно знайти корінь рівняння (1.5) тобто числа x*1 , x*2 ,..., які шляхом підстановки їх в (1.5) перетворюють рівняння у вірну числову рівність. Числа x*1 , x*2 ,... також називаються нулями функції f (x).
Умова існування кореня рівняння (1.5) походить з теореми:
Якщо неперервна функція f (x) приймає значення різних знаків на кінцях відрізку
13

[a,b], тобто f (a) f (b)< 0 , то всередині цього відрізку утримується, принаймні, один корінь рівняння f (x)= 0 . Тобто, знайдеться хоча б одне число x* (a,b) таке, що f (x* )= 0 . Якщо ж f (x) є неперервною і диференційовуваною та її перша похідна зберігає знак всередині відрізку [a,b], то на даному відрізку перебуває тільки один ізольований корінь (1.10) x = x* рівняння.
Ізольований корінь (1.10)
Ізольований корінь – це значення x , що задовольняє f (x)= 0 і не утримує інших коренів у своєму околі.
Таким чином, при знаходженні коренів рівняння (1.5) чисельним методом, крім неперервності f (x) передбачається:
1. Функція приймає на кінцях відрізку різні знаки; 2. Похідні f ' (x) й f " (x) неперервні на відрізку;
3. Похідні на відрізку не змінюють знака.
Геометрично остання умова означає, що передбачається одна із чотирьох схем (рис.
1.4).
а |
b |
а |
b |
а |
b |
а |
b |
Рис. 1.4. Геометрична інтерпретація знакосталості похідних
Наближене знаходження ізольованих дійсних коренів рівняння (1.5) здійснюється у два етапи:
1.Знаходять відрізки ai ,bi , всередині кожного з яких утримується один і тільки один корінь рівняння. Цей етап називається процедурою відділення коренів. По суті, на ньому здійснюється грубе знаходження кореню x = x*i .
2.Грубе значення кожного кореня x = x*i уточнюється до заданої точності одним із чисельних методів, у яких реалізуються послідовні наближення.
Перший етап значно складніше другого. Тому що не існує досить ефективних методів відділення всіх коренів. Найчастіше використають наступні способи знаходження відрізків ізоляцій: графічний (за допомогою побудови і дослідження графіків функцій); аналітичний (заснований на докладному дослідженні функції); метод послідовного перебору (заснований
14

на обчисленні функції із заданим кроком аргументу і виділенні тих відрізків, де функція змінює знак).
2.2. Відділення коренів
Відділення кореню починається із встановлення знаків f (x) у граничних точках об-
ласті визначення функції.
Після цього, або аналітично, або графічно, використовуючи особливості функції, знаходять значення функції в деяких проміжних точках x = x1 , x2 ,... і обирають інтервали, у
яких функція має різні знаки на кінцях інтервалу. За умовами вищевикладеної теореми в таких інтервалах існує корінь рівняння.
Після цього необхідно переконається в тім, що в кожному інтервалі перебуває тільки один корінь. У противному випадку змінювати інтервал.
ЗВЕРНІТЬ |
|
Якщо відомі корені рівняння f ' (x)= 0 , то процес відділення |
|
||
УВАГУ! |
|
коренів можна спростити. Для цього досить визначити знаки |
|
функції f (x) в точках нулів її похідної f ' (x)= 0 і гранич- |
|
NB ! |
|
|
|
них точках визначення функції x = a і x = b . |
|
ЗВЕРНІТЬ |
|
Дійсні корені рівняння f (x)= 0 можна відокремити приб- |
|
||
|
||
УВАГУ! |
|
лизно, як точки перетину графіком y = f (x) осі абсцис |
NB ! |
|
|
|
|
|
Цей метод зручний своєю наочністю, але при обчисленнях вручну ним не завжди можна скористатися, оскільки:
1.f (x) може являти собою функцію, графік якої побудувати дуже складно (наприклад, y = ex + sin x ).
2.Обмеженість розмірів креслення дозволяє знайти корінь тільки в деякому обмеженому проміжку.
Перший недолік можна усунути, якщо вдається записати вихідне рівняння f (x)= 0 у вигляді ϕ (x)= g (x), при якому графіки y =ϕ (x) і y = g (x) побудувати значно простіше. Тоді корені рівняння знаходять як абсциси точок перетинання графіків y =ϕ (x) і y = g (x).
Приклад. Відокремити корінь рівняння: x ln x = 1
Рішення. Запишемо це рівняння у вигляді ln x = 1x . Побудуємо графіки і визначимо точку їх перетинання (рис. 1.5).
Перевагою графічного методу (крім його наочності) є те, що часто він дає можливість оцінити кількість коренів і їх знаки.
15

2,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
|
|
|
|
|
|
|
Точка перетинання – корінь рів- |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
няння x ln x = 1 |
|
|
|
|
|
|
|
||||||
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
2 |
3 |
4 |
5 |
|
6 |
7 |
8 |
9 |
|
10 |
||||||||||
Рис. 1.5. |
Рішення рівняння x ln x = 1 . |
|
|
|
|
|
|
|
|
|
|
|||||||||||
2.3. Метод половинного ділення
 1/x
1/x
 ln(x)
ln(x)
ЗВЕРНІТЬ |
Інакше цей метод називають метод Больцано ділення навпіл |
|
УВАГУ! |
або метод бісекцій. |
|
|
|
|
NB ! |
|
|
|
|
|
Нехай дано рівняння f (x)= 0 , відомий відрізок [a,b] ізоляції кореня |
x* для даного |
|
рівняння, f (x) неперервна на відрізку [a,b]. Тоді графік функції y = f (x) |
перетинає вісь |
|
OX на відрізку [a,b] (початковому інтервалі невизначеності (1.11)) в крапці |
x* і значен- |
ня функції на кінцях відрізку мають різні знаки, тобто |
|
f (a) f (b)< 0 . |
(1.6) |
Початковий інтервал невизначеності (1.11)
Відрізок [a,b] називається початковим інтервалом невизначеності, тому що відомо, що корінь йому належить, але його місце розташування з необхідною точністю не визначено
Основна ідея методу бісекцій полягає у наступному: ділимо відрізок ізоляції навпіл і обираємо ту половину, де функція змінює знак, одержуємо новий відрізок ізоляції, довжина якого у два рази менше попереднього. Цю процедуру повторюємо доти, поки довжина відрізка ізоляції не стане менше заданої точності. Розглянемо це більш докладно.
|
|
Для знаходження кореня ділимо відрізок [a,b] навпіл. Якщо |
f |
a + b |
||||||
|
|
|
2 |
= 0 , то точка |
||||||
|
|
|
|
|
|
|
|
|
|
|
c = a + b |
є коренем. |
Вважаємо, що f (c)≠ 0 . Тоді оберемо ту |
з |
|
половинок відрізку |
|||||
|
2 |
|
|
|
|
|
|
|
|
|
|
a + b |
a + b |
|
|
|
|
|
|
||
a; |
2 |
|
або |
2 |
;b , на кінцях якої функція має різні знаки, і позначимо цей відрізок |
|||||
|
|
|
|
|
|
|
|
|
||
16

a1 ;b1 . Довжина цього відрізку дорівнює: b1 −a1 = b −2 a .
Відрізок a1 ;b1 знову ділимо навпіл і обираємо новий відрізок a2 ;b2 аналогічно. Будуємо послідовність відрізків an ;bn , кожний з яких вдвічі менше попереднього, таким чином одержимо послідовність вкладених друг у друга відрізків ai ;bi таких, що
f (ai ) f (bi )< 0 (i = 1,2,3,...,n).
Цей процес послідовного ділення навпіл продовжуємо доти, поки не виконається одна із двох умов:
1.Або знайдеться така точка cn = an +2 bn , у якій f (cn )= 0 і cn – точне значення кореню (на практиці виходить досить рідко).
2.Або на деякому кроці одержимо відрізок ізоляції an ;bn , довжина якого менше необхідної точності:
b |
−a |
|
= b −a |
< ε |
(1.7) |
n |
|
n |
2n |
|
|
Ліві кінці відрізків утворять монотонну неспадну послідовність an , а праві – bn , утворять монотонну незростальну послідовність. Отже, ці послідовності мають ту саму границю x* :
x* = lim an = lim bn
n→∞ n→∞
Підставляючи x* в (1.6) перейдемо до границь. Одержимо
lim f (an ) f (bn )= f (x* ) f (x* )< 0 .
n→∞
Це протиріччя, таким чином f (x* )= 0 .
Оскільки корінь належить відрізку ізоляції an ;bn , то в цьому випадку, будь-яке число із цього відрізку відрізняється від точного значення кореня менше, ніж на ε . Числа an і bn є наближеними значеннями шуканого кореня з нестачею і надлишком відповідно. Звичайно беруть як відповідь число із середини останнього відрізку ізоляції:
x* = |
an + bn |
= cn |
(1.8) |
|
|||
2 |
|
|
|
Можна заздалегідь оцінити кількість ділень навпіл вихідного відрізку. Оскільки щораз довжина відрізка зменшується у два рази, то по досягненні необхідної точності ε за n кро-
ків одержимо відрізок довжиною bn −an = b2−na < ε . Звідси можна виразити, злогарифмува-
вши, n :
|
|
b −a |
|
|
||||
|
|
lg |
ε |
|
|
|
||
n > |
|
|
|
(1.9) |
||||
lg 2 |
|
|
|
|
||||
|
|
|
|
|
|
|
||
Або |
|
|
|
|
|
|
|
|
n > |
lg (b −a) |
− |
lg ε |
|
|
(1.10) |
||
|
lg 2 |
|
||||||
|
|
lg 2 |
|
|
|
|
||
Із цієї формули можна оцінити кількість кроків. Крім того, з неї можна побачити, що |
||||||||
для того, щоб поліпшити точність у k разів, |
тобто припустивши, що ε* = |
ε |
, необхідно зро- |
|||||
|
|
|
|
|
|
|
k |
|
17

бити додатково n1 > lglg k2 кроків.
Основною перевагою методу бісекцій є надійність, стійкість до помилок округлення, відсутність обмежень на вид функції f (x) (потрібно тільки неперервність). Головний недо-
лік – повільна збіжність до точного рішення.
На практиці метод бісекцій використають у комбінації з яким-небудь швидкозбіжним методом: методом бісекцій спочатку грубо визначають початкове наближення, а потім застосовують швидкозбіжний метод (наприклад, метод Ньютона).
2.4. Реалізація метода половинного ділення в MS Excel
Приклад реалізації методу половинного ділення в середовищі Microsoft Excel наведено на рис. 1.6.
§ 3. Методи розв’язання нелінійних рівнянь: метод Ньютона
3.1. Постановка задачі
Якщо f (x), f ' (x) і f '' (x) безперервні в околі кореня, цю додаткову інформацію про властивості функції f (x) можна використати для побудови алгоритмів, які породжують
послідовності, що збігаються до кореня швидше, ніж при методі ділення навпіл. Метод Ньютона-Рафсона (або просто Ньютона, також має назви метод дотичних і метод ліне-
аризації (1.12)) є одним з найбільш корисних і найвідоміших алгоритмів, у якому використається неперервність першої і другої похідної. Він швидко збігається і допускає різні модифікації, пристосовані для рішення окремих задач. Однак, цей метод є ефективним при досить
жорстких обмеженнях на характер функції f (x):
Лінеаризація (1.12)
ЛІНЕАРИЗАЦІЯ (від лат. linearis — лінійний), один з найпоширеніших методів аналізу нелінійних систем (або залежностей), при якому вони розглядаються (з певними допущеннями) як лінійні.
|
|
|
1. |
існування другої похідної функції |
f (x) на множині G ={a ≤ x ≤ b}; |
2. |
задоволення першої похідної умові |
f ' (x)≠ 0 для всіх x G ; |
3. |
знакосталість f ' (x), f '' (x) для всіх x G . |
|
Геометрична інтерпретація методу Ньютона полягає в наступному. Задається початкове наближення x(0) . Далі проводиться дотична до кривої y = f (x) в точці x(0) (рис. 1.7),
тобто крива заміняється прямою лінією. Як наступне наближення обирається точка перетинання цій дотичній з віссю абсцис. Процес побудови дотичних і знаходження точок перетинання з віссю абсцис повторюється доти, доки приріст не стане менше заданої величини ε .
18
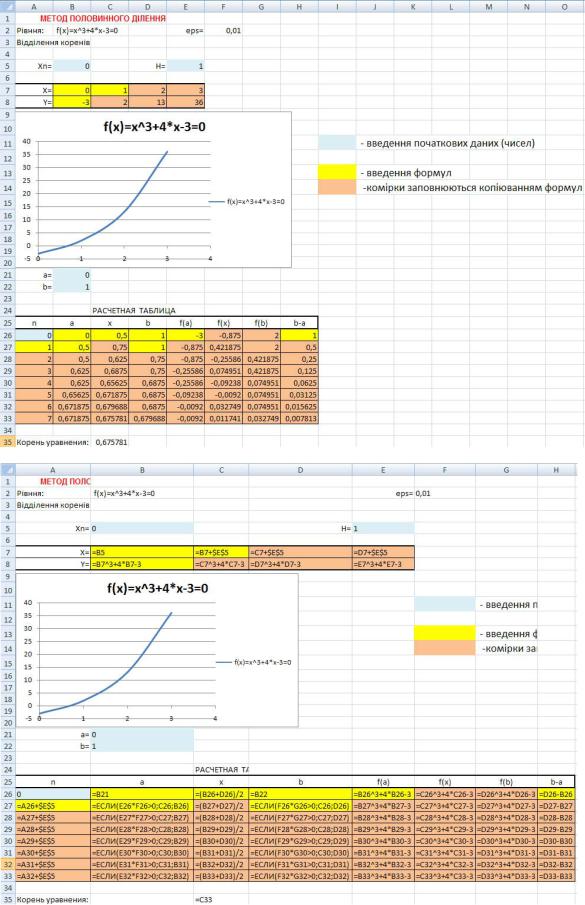
а)
б)
Рис. 1.6. Приклад розв’язання рівняння за методом половинного ділення в Microsoft Excel: а) вид листа Microsoft Excel; б) формули, що розташовано в комірках листа Microsoft Excel
19
