строймех часть1

42

Затем нужно отдельно рассчитать маленькую ферму, считая, что она опирается на узлы основной фермы, воспринимает свои собственные нагрузки Р, и, кроме этих нагрузок, усилие Sаб , которое следует направить по прямой, соединяющей центры опорных шарниров этой фермы (схема II)

Лекция 10 Линии влияния усилий в стержнях ферм

При построении линий влияния усилий в стержнях ферм необходимо иметь ввиду следующее:

1)подвижные грузы, на которые в дальнейшем будет рассчитываться ферма, могут перемещаться как по нижнему, так и по верхнему поясам фермы. В зависимости от этого, приходится строить линии влияния для ферм с "ездой" по нижнему или "ездой" по верхнему поясу;

2)так как ферма в основном загружается узловыми нагрузками, то и линии влияния для них должны строится с учетом особенностей, возникающих при узловой нагрузке.

Разработаны и применяются два метода построения линий влияния усилий в стержнях ферм – статический метод и кинематический. Мы рассмотрим только статический метод, как основной.

Порядок построения линий влияния усилий в стержнях ферм статическим методом состоит в следующем:

1)подвижный груз Р=1 устанавливается в произвольном узле фермы;

2)затем при таком расположении груза составляется зависимость величины усилия в исследуемом стержне от положения груза;

3)выражая эту зависимость (уравнение) в графическом виде, мы получим искомую линию влияния усилия в изучаемом стержне фермы.

Следует иметь в виду, что, как правило, приходится рассматривать не менее двух положений единичного груза, чтобы получить уравнения правой и левой прямых линий влияния.

Для получения этих уравнений приходится использовать различные способы расчета ферм: способ рассечения (моментных точек и проекций), способ узловых вырезов и др.

Рассмотрим приемы построения линий влияния в стержнях ферм с использованием этих способов.

Построение линии влияния в стержне фермы с использованием способа моментных точек

Построим линию влияния в раскосе Д фермы при "езде" Р=1 по низу. Решение.

1)Рассечем ферму через три стержня на две части - левую и правую.

2)Находим моментную точку для усилия Д – т.р. Д.

3)Дальнейший расчет производим в табличной форме.

43

Полученные уравнения показывают, что правую и левую прямые мы может строить,

соответственно, как линии влияния опорных реакций А и В, но ординаты которых должны быть умножены на постоянные коэффициенты

произведения ( Aa) и ( Bb ) представляют собой изгибающие моменты простой балки для сечения, которое расположено под моментной точкой (т.р. Д).

44

показывают, что для обоих прямых в числителях расположены значения балочных изгибающих моментов для сечения балки, расположенного под моментной точкой. Поэтому правые и левые прямые можно построить так, как правую и левую прямые линий влияния балочного изгибающего момента. Однако все их ординаты должны быть умножены на коэффициент ( ±1/ ρ). Поэтому для практических расчетов нередко применяют построение

линий влияния для ферм без предварительного составления таблицы.

Рекомендуемый порядок построения:

1)Под левой опорой фермы откладывается отрезок равный дроби, в числителе которой стоит кратчайшее расстояние от левой опоры до моментной точки, а в знаменателе - кратчайшее расстояние от моментной точки до исследуемого стержня.

2)Знак этой дроби определяют так: если реакция А и усилие в изучаемом стержне дают относительно моментной точки моменты одного направления, то знак дроби "-"; если же эти моменты направлены в разные стороны, то знак дроби - "+".

3)Вершину отрезка ( ±а/ ρ)нужно соединить с нулевым значением под правой опорой, что и дает правую прямую линии влияния.

4)Моментную точку необходимо спроецировать по вертикали на эту (правую) прямую и найденную точку соединить с нулевым значением под левой опорой - это и будет направление левой прямой.

5)Чтобы завершить построение линии влияния нужно узел грузового пояса, расположенный левее сечения снести на левую прямую, а узел расположенный правее сечения - на правую прямую и эти точки соединить передаточной прямой.

6)Если ферма имеет консоли, то правую и левую прямые продолжают до концов этих консолей.

Пример.

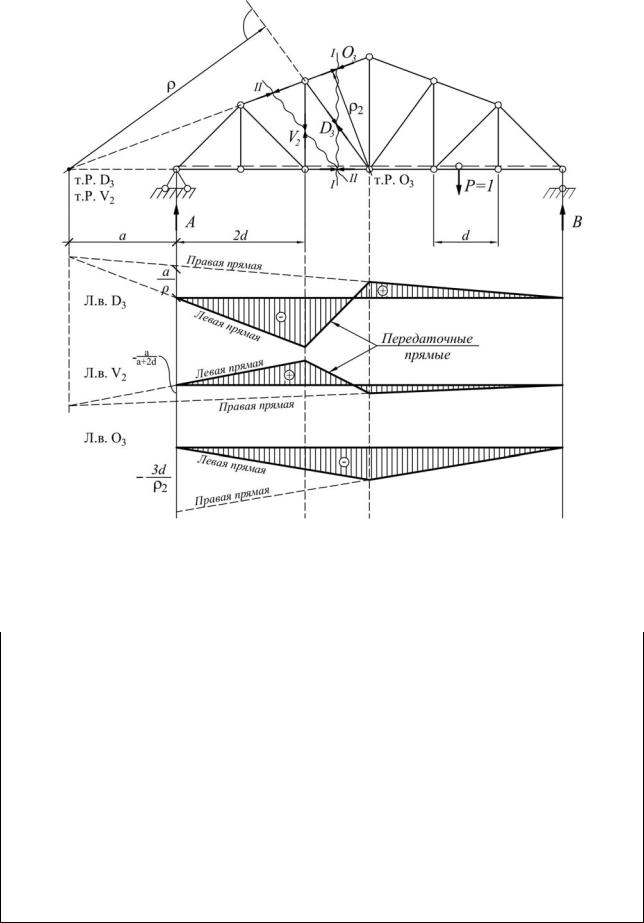
Построить линии влияния усилий в стержнях D2, V2, О3. Для построения линий влияния D2 и О3 проводим сечение I-I.

Строим линию влияния D2:

а) находим моментную точку; б) далее поступаем согласно вышеприведенному рекомендуемому порядку.

Строим линии влияния V2 (сечение II-II): Моментная точка та же.

Строим линии влияния О3 (сечение I-I). Моментная точка указана на рисунке.

45

Построение линий влияния усилий в стержнях ферм с применением способа проекций

Построить линии влияния D3 и V3.

Строим линии влияния V3 (сечение II-II), моментная точка в ∞

Левую и правую прямые строим соответственно как линии влияния опорных реакций

А и В.

Лекция 11 Построение линий влияния усилий в стержнях, расположенных на

консольных участках ферм

Задача: Построить линии влияния усилий в стержнях, расположенных на консольной части фермы (или в консольной ферме).

Особенностью построения линий влияния для таких стержней является следующее: где бы не располагался единичный груз (правее или левее сечения), мы должны всегда для составления формулы (зависимости) изменения усилия в изучаемом стержне рассматривать равновесие той части фермы, которая располагается в пределах от сечения до конца консольного участка фермы.

Построение линий влияния усилий в стержнях ферм с использованием способа вырезания узлов (способа узловых вырезов)

При построении линий влияния с использованием этого способа поступают следующим образом. Вырезают узел, к которому примыкает исследуемый стержень, а затем для этого узла рассматривают два случая расположения единичного груза:

а) когда груз Р=1 находится в вырезанном узле (если это возможно);

б) когда груз Р=1 отсутствует в данном узле (он находится в смежных узлах - либо правее, либо левее рассматриваемого узла).

Для каждого случая составляется уравнение статики и определяется усилие в исследуемом стержне. Анализ полученных усилий легко позволяет построить линию влияния.

48

Пример.

Построить линии влияния усилий (О1, V1, V3) в отмеченных стержнях фермы.

49

Построим линию влияния V1. Для этого вырежем узел "1" и рассмотрим два случая расположения нагрузки.

Случай 1:

груз Р=1 находится в вырезанном узле.

Из уравнения ∑Y = 0; V1 -1= 0 ; получаем V1 = 1

Случай 2:

груз Р=1 ушел из этого узла, тогда

∑Y =V1 = 0 ; V1 = 0

имеем V1 = 0

Строим линии влияния О1. Для этого вырежем опорный узел фермы. Рассмотрим случай, когда груз Р=1 где-то в пролете фермы, а не в опорном узле.

Составим уравнение ∑Y = 0.

О1 sinβ+ А = 0 , отсюда

О1 = −А sin1β

Это уравнение показывает, что пока груз движется между опорами фермы, линию влияния усилия О1 можно строить, как линию влияния опорной реакции , все ординаты

Теперь рассмотрим случай, когда груз Р=1 находится в опорном узле фермы.

Составим уравнение ∑Y = 0,

1+ А +О1 sinβ = 0 .

Но так как при этом положении груза опорная реакция А=1, то поэтому имеем: О1 sinβ = 0,

Строим линии влияния усилия V3.

Вырезаем коньковый узел фермы - узел "2". Несмотря на то, что в этом узле сходятся три стержня, и нагрузка в этот узел никогда не попадает, мы все же можем воспользоваться способ вырезания узлов для построения линий влияния V3.

Сделаем так. Выразим усилие V3 через усилия О3 и О4 в стержнях верхнего пояса, а затем построим линии влияния О3 (это просто сделать) и с помощью этой линии влияния построим линию влияния V3.

50

Составим уравнение

∑Х = 0 ; -О3cosα+О4cosα=0 ,

отсюда следует, что О3 = О4. Обозначим О3 = О4 = О. Составим уравнение

∑Y = 0; −2Osinα−V3 = 0,

отсюда следует, что V3 = O( −2sinα) .

Теперь построим линию влияния усилия О и все ординаты умножим на ( −2sinα) . Это и будет линия влияния для V3.

Лекция 12 Трехшарнирные системы

Трехшарнирная система состоит из двух дисков, соединенных между собой шарниром (С) и прикрепленных шарнирами (А и В) к земле.

Если диски I и II представляют собой криволинейные брусья, то такая система называется трехшарнирной аркой. Если дисками I и II являются ломаные стержни, то система называется трехшарнирной рамой.

Шарниры А и В называются опорными или пятовыми шарнирами, С - ключевой шарнир.

Расстояние между опорными шарнирами АВ по горизонтали называется пролетом арки или рамы. Расстояние от ключа до линии, соединяющей опорные шарниры, называется стрелой подъема арки f.

Если 0,1 ≤ lf ≤ 0,3 – пологие арки

0,3 < lf ≤1 – повышенные арки

Трехшарнирные системы являются статически определимыми системами, так как:

W= 3D - 2Ш0 - Соп = 3 2 - 2 1- 4=0

игеометрически неизменяемыми.

Трехшарнирные системы - это распорные системы, так как в их опорах, даже при отсутствии вертикальной нагрузки, возникают горизонтальные составляющие опорных реакций.