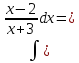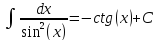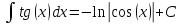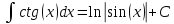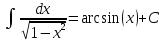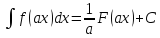Lection16

Лекция 16. «Неопределенный интеграл»

#1. Первообразная и неопределенный интеграл.

Определение 1.1. Функция 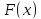называется первообразной от функции на отрезке 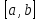, если для каждой точки отрезка выполняется равенство

т.е. производная от первообразной функции равна самой функции.

Пример. Найти первообразную от функции .

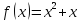Из определения первообразной следует, что искомой является функция . Это легко проверить, вычислив производную функции :

Заметим, что функции или 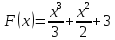тоже являются первообразными функции . Все дело в том, что производная постоянной величины равна 0.

Очевиден (не требует доказательства) следующий факт. Если функция является первообразной от функции , то функция , тоже является первообразной функции

Не очевидно, но имеет место следующее утверждение.

Теорема. Если и — две первообразные от функции на отрезке , то разность между ними равна постоянному числу:

Определение 1.2. Если функция является первообразной от функции , то выражение называется неопределенным интегралом от функции .

Таким образом, неопределенный интеграл это не одна, а целое семейство функций отличающихся между собой на постоянную величину. Если построить графики этих функций, то мы получим набор кривых сдвинутых по отношению друг к другу вдоль оси .

Замечание. Не всякая функция имеет первообразную, но если функция непрерывна на отрезке , то она имеет первообразную и неопределенный интеграл.

Определение 1.2. Интегрированием называется нахождение интеграла для данной функции.

Из определения неопределенного интеграла следуют следующие очевидные свойства неопределенных интегралов.

1. Производная от неопределенного интеграла равна подынтегральной функции, т. е. если , то

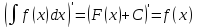
2. Дифференциал от неопределенного интеграла равен подынтегральному выражению:

Напомним, что дифференциал функции вычисляется по формуле:

или

3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная:

#2. Таблица интегралов.

Приведем таблицу интегралов от простейших функций.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

Проверим правильность некоторых интегралов. Для этого найдем производные правых частей у некоторых формул. При вычислении производных во всех формулах будем использовать то, что производная константы равна нулю: .

1. 

7. 

16.

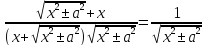
#3. Свойства неопределенных интегралов.

Приведем несколько свойств неопределенных интегралов.

Теорема 3.1. Неопределенный интеграл от алгебраической суммы двух или нескольких функций равен алгебраической сумме их интегралов:

Истинность этого утверждения очевидна. Производная суммы двух функция равна сумме производных, а операция интегрирования противоположна операции дифференцирования.

Пример. Вычислить интеграл.

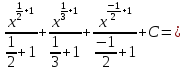
Теорема 3.2. Постоянный множитель можно выносить за знак интеграла, т. е., если , то:

Истинность этого утверждения также очевидна. Константу можно выносить за знак производной, а операция интегрирования противоположна операции дифференцирования.

Пример. Вычислить интеграл.

При вычислении неопределенных интегралов бывает полезно иметь в виду следующие правила. Если

то:

1. 

2. 

3. 

Пример. Вычислить интеграл.

(используем правило №1)

Пример. Вычислить интеграл.

(используем правило №2)

Пример. Вычислить интеграл.

(используем правило №3)

#4. Примеры вычислений интегралов.

Вычислим несколько интегралов на применение этих правил и таблицы производных

Пример. Вычислить интеграл.

Пример. Вычислить интеграл.

Пример. Вычислить интеграл.

Пример. Вычислить интеграл.