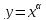Lection10

Лекция №10

Производная функции.

1. Задача о скорости движущейся точки.

Пусть функция

представляет закон прямолинейного движения материальной точки. Т.е. - это расстояние от некоторой начальной позиции до текущей позиции точки, которое точка преодолела за время . Предположим, надо найти скорость в этот момент времени. Для этого измерим расстояние через время . Очевидно, это расстояние равно

Следовательно, за время точка преодолела расстояние

Средняя скорость движения точки за период времени равна

Очевидно, что даже в период времени скорость меняется и в общем случае она не равна скорости в момент времени . Но, также можно утверждать, что средняя скорость настолько точно отражает скорость в момент времени , насколько время мало. Поэтому под скоростью в момент времени , можно считать величину

2. Определение производной.

Рассмотрим функцию

Предположим, аргумент функции изменился на некоторую величину . Новое значение аргумента функции есть . Величина называется приращением аргумента. Новое значение функции

Следовательно, функция изменилась на величину

Эта величина называется приращением функции.

Определение. Производной функции в точке называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремиться к нулю.

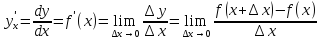
Замечание. При определении производной иногда используют другие обозначения. Если надо определить производную в точке , то вводятся обозначения

Пример. Найти производную функции

при .

Решение.

Подставляем значение аргумента

3. Графическая интерпретация производной.

Касательная

Угол наклона секущей

где - угол наклона секущей.

Если приращение аргумента 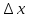устремить к 0, то секущая будет приближаться к касательной и в пределе совпадет с ней. Так как производная это предельное значение величины

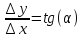
то производная – это тангенс угла наклона касательной.

Из этого утверждения следует, что уравнение касательной в точке для функции

имеет вид

Уравнение нормали в точке для функции

имеет вид

Пример. Написать уравнение касательной и нормали функции

при

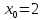
Решение.

Из предыдущего примера известно, если

то

Следовательно, в нашем случае

Уравнение касательной

Уравнение нормали

Определение. Если функция имеет производную в точке, то она называется дифференцируемой в точке.

Связь дифференцируемости и непрерывности.

Утверждение. Если функция дифференцируема в точке, то она непрерывна в точке. Обратное утверждение неверно.

Пример функции непрерывной, но не дифференцируемой в точке

Эта функция непрерывна при любом значении аргумента, дифференцируема для всех значений аргумента за исключением 0.

т.е. предела нет

4. Правила дифференцирования.

4.1. Константу можно выносить за знак производной.

4.2. Производная суммы (разности) двух функций равна сумме (разности) производных этих функций

4.3. Производная произведения двух функций вычисляется по формуле

4.4. Производная отношения двух функций вычисляется по формуле

Доказательство 4.3.

4. Таблица производных.

Функция	Производная