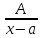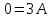Lection18

Лекция 18 Интегрирование рациональных дробей. Интегрирование тригонометрических функций.

#1. Понятие рациональной дроби.

Определение. Рациональной дробью называется выражение вида

Цель настоящей лекции – научиться вычислять интегралы от подобных функций.

В общем случае старшая степень многочлена, стоящего в числителе () может быть выше старшей степени многочлена, стоящего в знаменателе (). В случае, когда степень числителя выше степени знаменателя (), простым преобразованием (делением) можно преобразовать рациональную дробь так чтобы она имела вид:

где .

Пример. Преобразовать рациональную дробь

к виду, где степень числителя будет ниже степени знаменателя.

Решение. Выражение в числителе можно представить в виде

Исходную дробь можно преобразовать к виду.

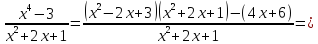
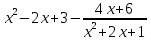
Как видно из последней формулы, после преобразования, получается многочлен и рациональная дробь, в которой в числителе степень ниже, чем в знаменателе. Интеграл от многочлена вычисляется при помощи табличных интегралов. А полученная рациональная дробь может быть разложена на простейшие.

#2. Интегрирование простейших рациональных дробей.

Определение. Простейшими рациональными дробями называются дроби вида.

1
2
3
4

Рассмотрим интегрирование простейших рациональных дробей.

Решение интеграла

было рассмотрено в предыдущей лекции.

Рассмотрим методику вычисления интеграла

Заметим, что показатель степени в знаменателе, целое число больше и равно 2. Метод решения заключается в том, что этот интеграл преобразуется к табличному интегралу и интегралу со степенью знаменателя на 1 меньше.

Шаг №1. Попробуем удалить из числителя. Для этого преобразуем числитель к следующему виду.

Подставляем это выражение в последний интеграл.

Шаг №2. Вычисляем первый интеграл, сделав замену переменных

Получаем:

Шаг №3. С этого шага начинаем преобразовывать второй интеграл для того, чтобы понизить степень в знаменателе на единицу. Для упрощения расчетов, выпишем этот интеграл без числового коэффициента.

В знаменателе выделим полный квадрат и подставим в интеграл

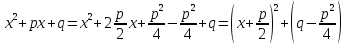
Сделаем замену переменных

Получаем интеграл

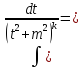
Шаг №4. Делаем ключевое преобразование, понижающее степень знаменателя.

Заметим, что первый интеграл отличается от исходного интеграла тем, что степень в знаменателе на единицу меньше чем у исходного интеграла. Применяя аналогичные преобразования к первому интегралу несколько раз, можно понизить степень до 1 и посчитать интеграл, ранее описанным методом. Выпишем последний интеграл отдельно:

Вычисляем этот интеграл «по частям»: .

Применяем формулу интегрирования по частям.

После этого получаем интеграл, имеющий в знаменателе степень на единицу меньше, чем была ранее. Повторяя подобный алгоритм несколько раз, можно прийти к интегралу вычисляемому по таблице.

Пример. Вычислить интеграл.

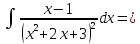
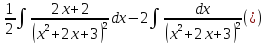
Выписываем первый интеграл

Делаем замену переменных

Выписываем второй интеграл.

В знаменателе выделяем полный квадрат

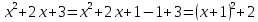
и подставляем в интеграл

Преобразуем, используя

Первый интеграл вычисляется

Второй интеграл

вычисляем по частям ( )

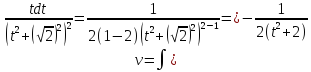
Подставляем в интеграл

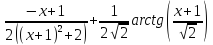
Подставляем оба, ранее вычисленных интеграла, в исходный интеграл

#2. Разложение рациональных дробей на простейшие.

Разложение рациональной дроби на простейшие дроби основано на следующем утверждении.

Утверждение. Любой многочлен с действительными коэффициентами

может быть представлен в следующем виде (разложение на множители):

где, - действительные числа. Причем, дискриминант, в квадратных трехчленах меньше нуля. Такое представление многочлена называется разложением многочлена на простейшие множители.

При разложении рациональной дроби на простейшие дроби используется метод неопределенных коэффициентов. Он заключается в том, что рациональная дробь записывается в виде суммы простейших дробей со знаменателями, взятыми из разложения своего знаменателя. Вместо числителей используются неопределенные коэффициенты. Затем, составляется система линейных уравнений относительно этих коэффициентов.

Каждому сомножителю из разложения знаменателя соответствует «свой» набор дробей

Пример. Вычислить интеграл

Разложим знаменатель на множители

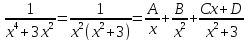
Приведем правую часть к общему знаменателю и приравняем числители

Приравняем коэффициенты при равных степенях

Вычисляем коэффициенты.

Подставляем коэффициенты в интеграл

#3. Вычисление простейших тригонометрических интегралов.

При вычислении простейших тригонометрических интегралов можно использовать следующие формулы преобразований.

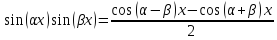
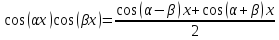
Пример. Вычислить интеграл

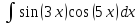
Для вычисления интеграла применим последнюю из вышеуказанных формул, где

Для понижения четного порядка тригонометрической функции, используются формулы, которые называются формулами понижения степени.

Пример. Вычислить интеграл

Применим 2-ю формулу с .

Первые два интеграла табличные, а к третьему интегралу снова применяем формулу понижения степени

Если под интегралом некоторая функция из тригонометрических функций в нечетной степени, то интеграл от тригонометрических функций сводится к интегралу от рациональных функций, путем замены или Причем, надо учесть следующую формулу

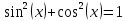
Пример. Вычислить интеграл

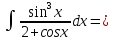
Вычисление интеграла от тригонометрических функций в общем случае.

Замена

Из этой замены, получаем

Учитываются формулы

В итоге получаем

Пример. Вычислить интеграл

Применим, вышеприведенные формулы