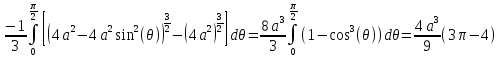Lection22
.docxЛекция 22. Двойные интегралы.
-
Определение двойного интеграла.
Предположим функция двух переменных
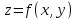
определена
на некоторой плоской области D. Разобьем
произвольным образом эту область на
отдельные участки и для каждого такого
участка, вычислим значение функции в
некоторой, произвольной, внутренней
точке. Для каждого участка умножим
значение функции во внутренней точке
на площадь участка и полученные
произведения просуммируем.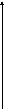









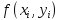
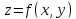
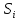



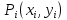
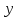

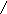

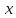
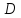
Полученная сумма называется интегральной суммой, соответствующей данному разбиению и выбору внутренних точек.
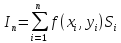
Заметим,
что интегральная сумма численно равна
объему цилиндрического тела, ограниченного
снизу плоской областью
 ,
а сверху поверхностью значений функции.
Если мы выберем более мелкое разбиение
области, то, очевидно, значение объема
будет вычислено более точно.
,
а сверху поверхностью значений функции.
Если мы выберем более мелкое разбиение
области, то, очевидно, значение объема
будет вычислено более точно.
Определение.
Если существует конечный предел
интегральных сумм, когда площадь
максимального участка разбиения области
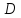 стремится к нулю, то функция называется
интегрируемой в области
стремится к нулю, то функция называется
интегрируемой в области
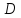 ,
а предел называется двойным интегралом
по области
,
а предел называется двойным интегралом
по области
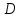 .
.
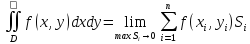
Утверждение.
Если функция непрерывна на замкнутой
области
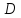 ,
то функция интегрируема на этой области.
,
то функция интегрируема на этой области.
Свойства двойного интеграла.
Теорема. Двойной интеграл от суммы двух функций равен сумме двойных интегралов от этих функций
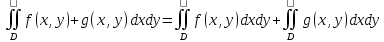
Теорема. Константу можно выносить за знак двойного интеграла
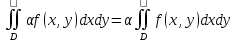
Теорема.
Если область
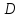 можно представить в виде объединения
двух непересекающихся областей
можно представить в виде объединения
двух непересекающихся областей
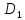 и
и
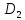 ,
а функция непрерывна на области
,
а функция непрерывна на области
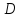 ,
то интеграл по области
,
то интеграл по области
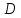 равен сумме интегралов по составляющим
областям.
равен сумме интегралов по составляющим
областям.
-
Вычисление двойного интеграла.
Вычисление двойного интеграла обычно сводится к вычислению двух обычных одномерных интегралов.
Пусть
область
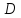 ограничена графиками двух функция на
некотором отрезке
ограничена графиками двух функция на
некотором отрезке
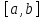 ,
т.е. имеет вид
,
т.е. имеет вид
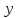

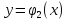
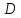
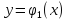
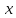

В этом случае, двойной интеграл можно вычислить по следующей формуле
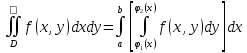
Пример. Вычислить двойной интеграл
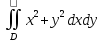
где,
область
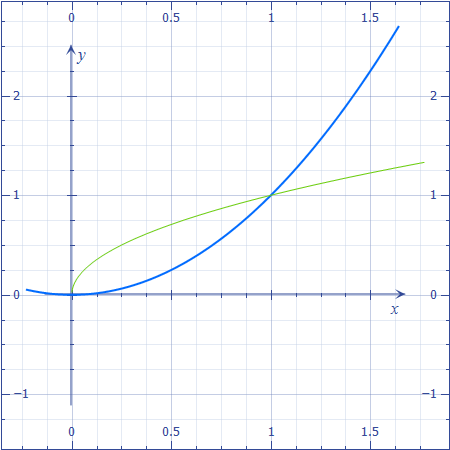
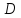 ограничена двумя функцыями
ограничена двумя функцыями
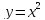
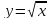
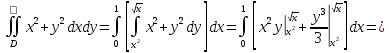
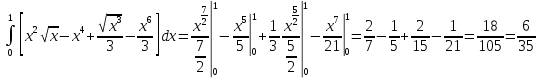
Пусть
область
 ограничена графиками двух функция на
некотором отрезке
ограничена графиками двух функция на
некотором отрезке
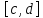 на оси
на оси
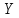 ,
т.е. имеет вид
,
т.е. имеет вид
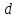
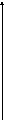
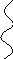
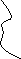
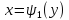
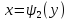
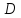
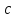

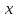

В этом случае, двойной интеграл можно вычислить по следующей формуле
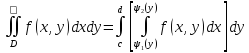
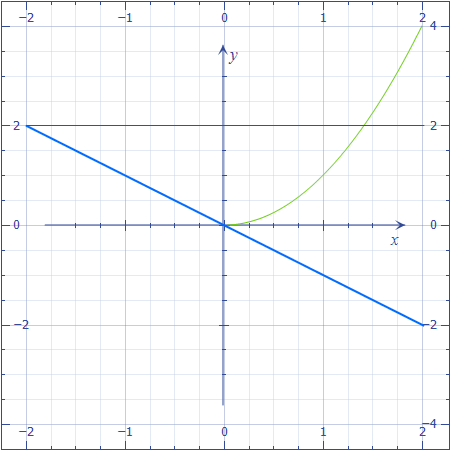
Пример. Вычислить двойной интеграл.
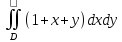
где,
область
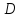 ограничена двумя функциями
ограничена двумя функциями
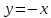
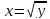

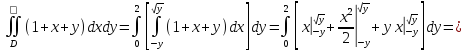
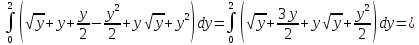
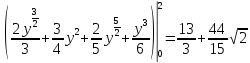
-
Вычисление объема при помощи двойного интеграла.
Как
следует из определения двойного
интеграла, его физический смысл это
объем тела между поверхностью - графиком
функции и плоскостью
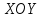 .
Нужно заметить, что при вычислении
объема с помощью двойного интеграла
нужно учитывать знак функции. Так объем
тела выше координатной плоскости
учитывается со знаком «+», а объем тела
ниже координатной плоскости учитывается
со знаком «-».
.
Нужно заметить, что при вычислении
объема с помощью двойного интеграла
нужно учитывать знак функции. Так объем
тела выше координатной плоскости
учитывается со знаком «+», а объем тела
ниже координатной плоскости учитывается
со знаком «-».
Пример. Вычислить объем тела ограниченного следующими плоскостями
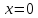 ,
,
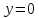 ,
,
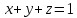 ,
,
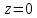
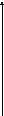

1
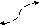
1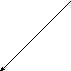
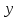



1
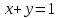
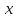
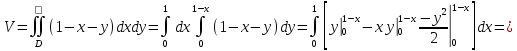
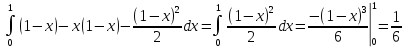
Если тело заключено между двумя поверхностями, то его объем равен двойному интегралу разности функций, определяющих эти поверхности.
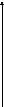



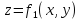


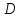


Пример. Определить объем тела, ограниченного поверхностями
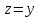
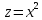

Решение. Найдем область интегрирования, для этого приравняем правые части двух первых уравнений. Очевидно, область интегрирования определяется следующими уравнениями
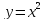
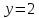
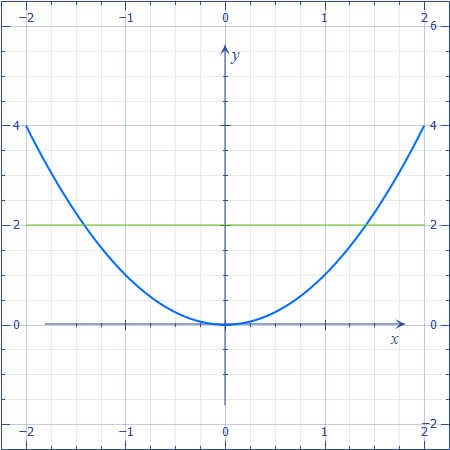
Для того, чтобы определить пределы интегрирования, решим уравнение
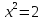
Следовательно, область интегрирования можно задать неравенствами
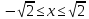
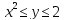
Тело ограничено сверху плоскостью
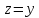
Снизу тело ограничено цилиндрической поверхностью

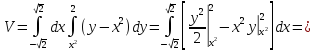
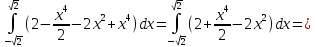

Замечание. Если функция тождественно равна 1, то ее двойной интеграл равен площади области интегрирования, т.е.

-
Вычисление двойного интеграла в полярной системе координат.
В
некоторых случаях для вычисления
двойного интеграла необходимо перейти
к полярной системе координат. В полярной
системе координат положение точки
определяется двумя числами
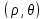 .
Первое из этих чисел это радиус вектор
– расстояние от точки до начала координат.
Второе из этих чисел это угол наклона
вектора точки над осью
.
Первое из этих чисел это радиус вектор
– расстояние от точки до начала координат.
Второе из этих чисел это угол наклона
вектора точки над осью
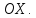
Полярная система координат связана с декартовой системой координат следующими формулами
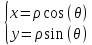
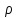


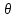

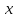

Переход к полярной системе координат при вычислении двойного интеграла необходим в том случае, если область интегрирования «правильная» в полярной системе координат


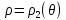

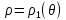



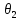
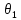
Правильная, в полярной системе координат, область имеет вид сектора и может быть задана неравенствами
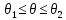

Формула перехода от декартовой системы координат к полярной системе координат имеет вид.
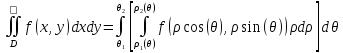
Пример. Вычислить обьем тела, ограниченного следующими поверхностями
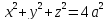
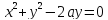
Заметим, что второе уравнение можно переписать в виде
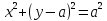
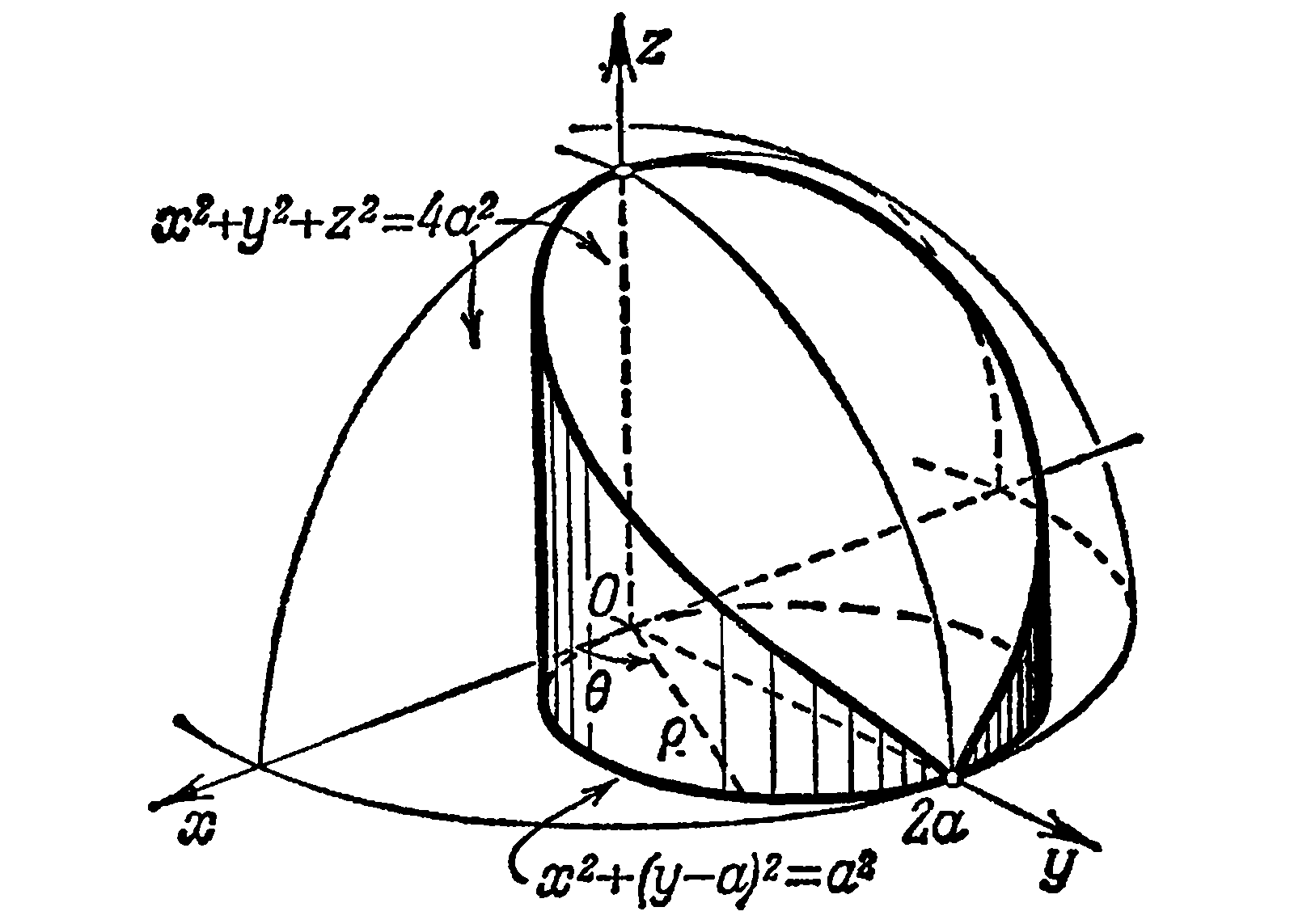
Если вычислять объем декартовой системе координат, то расчет выглядит следующим образом
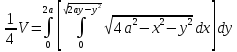
Полученные интегралы сложны для вычисления. Перейдем к полярной системе координат.
Пределы
интегрирования по переменной
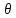
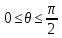
Для
нахождения пределов интегрирования по
переменной
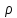 подставим формулы перехода к полярной
системе координат в уравнение второй
поверхности
подставим формулы перехода к полярной
системе координат в уравнение второй
поверхности
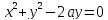
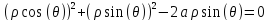
Получаем
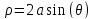
Следовательно
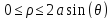
Двойной интеграл в полярной системе координат будет иметь вид.