Lection21

Лекция 21. Несобственные.

1. Определение несобственного интеграла.

Пусть функция

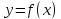
определена и непрерывна для всех значений аргумента больших числа , т.е для всех значений

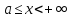
Рассмотрим интеграл на отрезке

Так как подынтегральная функция непрерывна на любом отрезке 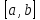, то такой интеграл существует для любого значения Это значит, что функция 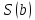существует на полуоси

и можно вычислять предел

Определение. Если существует конечный предел

то, этот предел называется несобственным интегралом от функции на интервале и обозначается таким образом

Другими словами

Предел может, как существовать, так и не существовать или быть бесконечным. Если предел существует, то несобственный интеграл называется сходящимся, если предел не существует или существует, но равен бесконечности, то интеграл называется расходящимся.

Аналогично, можно ввести понятие несобственного интеграла на интервале

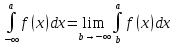
Несобственный интеграл на всей числовой оси можно представить в виде суммы двух несобственных интегралов

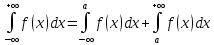
Пример. Вычислить несобственный интеграл.

Так как определенный интеграл на конечном отрезке это площадь под графиком отрезка, то несобственный интеграл, это площадь неограниченной фигуры, под графиком на бесконечном интервале. В нашем примере, несобственный интеграл это площадь под графиком следующей функции

Пример. Вычислить, при каких значениях параметра 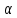несобственный интеграл сходится.

Рассмотрим случай, когда

При

Следовательно, несобственный интеграл сходится при .

Графики функций

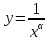
2. Интеграл от разрывной функции.

Предположим, функция

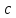определена на интервале . В правой точке функция не определена или имеет разрыв второго рода. Рассмотрим предел

Этот предел может, как существовать, так и не существовать. Если этот предел существует, то он определяет несобственный интеграл

Если предел не существует, то этот несобственный интеграл называется расходящимся.

Аналогично, можно определить несобственный интеграл, если точка разрыва находится слева от области определения функции, т.е. функция , определена на интервале

Если точка разрыва, например , находится внутри отрезка ,

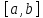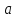
то интеграл надо развить на два несобственных интеграла.

Пример. Вычислить несобственный интеграл

Заметим, что этот интеграл именно несобственный, так как знаменатель обращается в ноль при значении . Т.е. эта точка является точкой разрыва второго рода

График функции

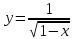
3. Свойства несобственных интегралов.

Теорема 1. Если на области интегрирования ( это точка разрыва или ) выполняется неравенство

то,

- из сходимости несобственного интеграла

следует сходимость несобственного интеграла

- из расходимости несобственного интеграла

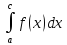
следует расходимость несобственного интеграла

Теорема 2. Если сходится несобственный интеграл от модуля функции

то сходится несобственный интеграл от самой функции

Пример. Исследовать на сходимость интеграл.

Заметим, что интеграл является несобственным, так как знаменатель подынтегральной функции обращается в ноль при значении аргумента равным нижнему пределу интегрирования.

Сравним значение подынтегральной функции с функцией, неопределенный интеграл от которой мы можем вычислить, а значит, и проверить на сходимость - расходимость.

Интеграл от правой функции мы можем посчитать

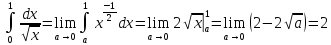
Так как интеграл от большей функции сходится, то исследуемый интеграл сходится также.