Lection17

Лекция «Методы интегрирования простейших функций»

#1. Интегрирование методом замены переменных.

В некоторых случаях, при вычислении неопределенного интеграла, невозможно сразу применить формулу из таблицы интегралов или свести вычисление интеграла к простейшим интегралам. В этих случаях необходимо применять различные приемы и методы вычисления интегралов. Одним из таких методов и, вероятно, самым распространенным, есть замена переменных в неопределенном интеграле. Этот метод заключается в следующем. Предположим, надо вычислить интеграл

Подбираем функцию и подставляем ее в интеграл, учитывая что .

Правильно подобрав функцию , можно добиться того, что полученный интеграл будет табличным.

Пример. Вычислить интеграл

Сделаем замену 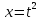, После такой замены интеграл примет вид.

Замечание. Часто, при вычислении интеграла, подбирается функция . Это делается в том случае, если интеграл имеет вид

,

где функция легко интегрируема. В этом случае имеем следующее преобразование: . Подставляем в интеграл и получаем:

Пример. Вычислить интеграл.

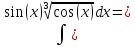
Делаем замену переменных: Вычисляем

Подставляем в интеграл выражения относительно

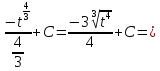
Вместо переменной подставляем функцию , которую использовали при замене переменных.

Пример. Вычислить интеграл.

Сделаем замену Вычисляем

Подставляем замену в исходный интеграл.

Вместо переменной подставляем функцию , которую использовали при замене переменных.

Пример. Вычислить интеграл.

Сделаем замену Вычисляем

Подставляем замену в исходный интеграл.

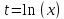Вместо переменной подставляем функцию , которую использовали при замене переменных.

#2. Интегрирование простейших дробей с квадратным трехчленом.

2.1. Рассмотрим интеграл вида.

Этот интеграл можно преобразовать к следующему интегралу

Поэтому в дальнейшем будем рассматривать интегралы подобного типа, когда перед стоит 1.

Рассмотрим методику вычисления интеграла вида

Преобразуем знаменатель, выделив полный квадрат:

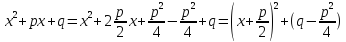
Подставляем выражение в интеграл

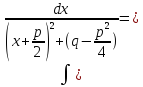
Делаем замену переменных 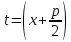; 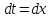. При этом учтем знак выражения может быть как положительным, так и отрицательным. Обозначим модуль (положительную часть) этого выражения через . В итоге последний интеграл может быть записан в виде:

Это табличный интеграл и, в зависимости от знака могут быть применены следующие формулы:

(*)

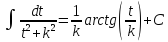Пример. Вычислить интеграл.

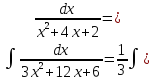
Выделим полный квадрат из знаменателя:

Подставляем это выражение в знаменатель интеграла.

Применим формулу (**).

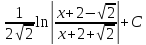
2.2. Рассмотрим интеграл вида.

Данный интеграл преобразуется и табличному интегралу вида

и к интегралу предыдущего (2.1) вида.

Вычислим производную знаменателя.

Преобразуем числитель таким образом, чтобы в нем «появился» знаменатель

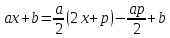
Подставляем это выражение в числитель и разбиваем на два интеграла

Рассмотрим каждый интеграл отдельно. Для вычисления первого интеграла

сделаем замену переменных .

Подставляем эти выражения в интеграл

Во втором интеграле в числителе стоит число, и решение этого интеграла рассмотрено в предыдущем пункте (2.1).

Пример. Вычислить интеграл.

Вычисляем производную знаменателя.

Преобразуем числитель интеграла, так чтобы там появилось выражение производной и разбиваем интеграл на два.

Вычислим каждый интеграл отдельно. Сначала первый.

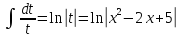
Второй интеграл

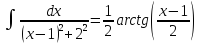
Подставляем вычисленные интегралы в исходный интеграл – продолжаем формулу (***).

2.3. Рассмотрим интеграл вида.

Для вычисления подобного интеграла необходимо выполнить действия, описанные в пункте 2.1 (т.е. выделить полный квадрат). Но в результате подобных действий получатся другие табличные интегралы

или

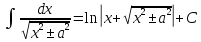
2.4. Рассмотрим интеграл вида.

Для вычисления подобного интеграла необходимо выполнить действия, описанные в пункте 2.2. Но в результате этих действий получатся другие табличные интегралы.

#3. Интегрирование по частям.

Из формулы производной произведения следует, что

Проинтегрируем левую и правую части

Учитывая, что

,

Получаем формулу интегрирования по частям

Пример. Вычислить интеграл.

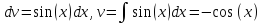
Пример. Вычислить интеграл.