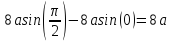Lection20

Лекция 20. Применение определенного интеграла.

#1. Вычисление площади при помощи определенного интеграла.

Как известно, из предыдущей лекции, определенный интеграл это площадь криволинейной трапеции между графиком функции и осью абсцисс. Но применять это свойство интеграла нужно осторожно.

Пример. Вычислить площадь фигуры между функцией

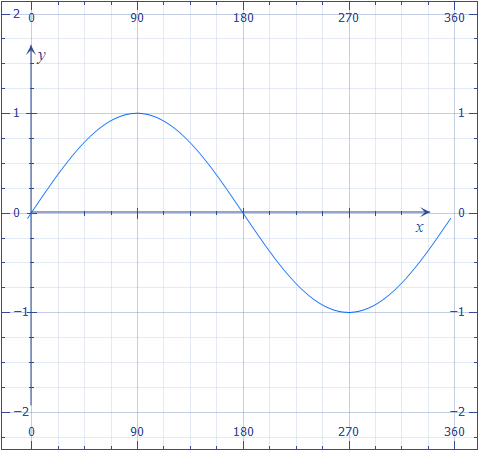
и осью OX на отрезке

Попробуем решить эту задачу «в лоб». Очевидно, что такой резудьтат не может быть правильным результатом. Причина в графике функции Площадь между функцией и осью абсцисс состоит из двух частей. Первая часть это площадь на отрезке , вторая часть это площадь на отрезке . Как видно из графика, обе площади равны. Но когда мы вычисляем интеграл по отрезку , то вторая площадь входит в интеграл с отрицательным знаком и в итоге получается 0. Правильное решение Тот же результат, можно получить, используя следующую формулу:

Этот пример иллюстрирует следующий подход к вычислению площадей – площадь расположенная ниже оси абсцисс входит в интеграл с отрицательным знаком. Поэтому следует разделять положительную и отрицательную составляющие интеграла.

Вычисление площади фигуры, образованной графиками двух функций.

Если необходимо вычислить площадь фигуры, образованную графиками двух функци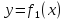й и ,

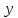
то следует применить следующую формулу.

Пример. Вычислить площадь фигуры, ограниченную следующими кривыми

Графики этих функций

Точки пересечения графиков функций находятся из решения уравнения:

Значения и являются очевидными решениями данного уравнения.

Площадь фигуры между графиками можно вычислить по формуле

#2. Вычисление площадей при параметрическом задании функции.

Предположим, площадь может быть вычислена при помощи интеграла

А подынтегральная функция может быть представлена в параметрическом виде

При этом

Площадь может быть вычислена при помощи интеграла

Пример. Вычислить площадь эллипса

Выделяем из формулы

Переменная изменяется на отрезке . Площадь можно вычислить по формуле

Но, эллипс имеет следующее параметрическое представление

Применим формулу (*), но при этом надо учесть отрезок для переменной x соответствует отрезку .

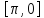#3. Вычисление площадей в полярной системе координат.

Напомним, что в полярной системе координат положение точки на плоскости определяется двумя параметрами: – расстояние от точки до начала координат и – угол наклона радиус вектора точки (вектор от начала координат до точки) к оси абсцисс.

Полярная система координат связана с декартовой системой координат следующими формулами

И обратное соотношение

Предположим, в полярной системе координат задана функция на отрезке .Заметим, что в полярной системе координат отрезок определяет некоторый сектор. Площадь в полярной системе координат определяются формулой.

Пример. Вычислить площадь фигуры, ограниченную лемнискатой

Очевидно, площадь этой фигуры равна сумме площадей четырех равных частей

#4. Вычисление длин дуг при помощи определенного интеграла.

Если нужно вычислить длину некоторой кривой, то подход для решения этой задачи принимается такой же, как и в случае вычисления площадей. Кривую разбивают на отдельные части, считают эти части отрезками прямой, вычисляют длины этих отрезков и суммируют их длины. Результат будет тем более точным, чем меньшие по длине отрезки участвуют в разбиении.

В результате этого подхода получаем следующие формулы для вычисления длин дуг.

1. Кривая задана функцией 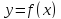на отрезке .

2. Кривая задана параметрическим способом на отрезке :

3. Кривая задана в полярной системе координат :

Пример. Вычислить длину окружности

1-й способ.

Представим уравнение окружности в виде «явной» функции.

Для применения первой формулы найдем производную функции

Кроме того, интегралом будем вычислять только четвертую часть от всей длины кривой, ту часть, которая лежит в первой четверти.

2-й способ.

Уравнение окружности в параметрической форме имеет вид

где, 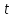это угол радиус-вектора точки с осью абсцисс: .

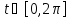Вычислим производные

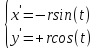
Как и в предыдущем примере, интеграл будет вычислять только четвертую часть от всей длины.

3-й способ.

Уравнение окружности в полярной системе координат имеет вид

Заметим, что функция , поэтому .

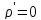Пример. Вычислить длину кардиоиды.

,

Вычисляем производную

Подставляем в интеграл и учитываем, что интеграл будет вычислять только половину дуги.