2.2. Некоторые теоремы теории вероятностей.

Одним из основных понятий теории вероятностей является событие, под которым понимается всякий факт, который может произойти и не произойти.

Практически невозможное событие - это событие, вероятность которого весьма близка к нулю.

Практически достоверное событие - событие, вероятность которого весьма близка к единице. Несколько событий называются несовместимыми, если никакие два из них не могут появиться вместе.

Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:

или для любого числа несовместных событий:

Если же события А и В совместны, то вероятность их суммы:

где Р(АВ) - вероятность произведения двух событий. Произведение - совместное появление двух событий.

Вероятность произведения независимых событий равна произведению вероятностей этих событий:

или используя знак произведения П, получим:

Эти теоремы часто используют в расчетах надежности технических систем.

Пример 2.2.1. Уменьшение расхода воздуха, проходящего через фильтросные пластины, возможно вследствие: закупорки твердыми частицами пор пластин (А); кольматажа (В); технологических дефектов (С). Их вероятности: Р(А)=0,10; Р(В)=0,02; Р(С)=0,30. Определить вероятность уменьшения расхода воздуха по сравнению с расчетным.

Решение: Появление любого из событий вызывает уменьшение расхода воздуха, проходящего через фильтросные пластины. События А, В и С могут быть несовместимыми, поэтому вероятность уменьшения расхода равна сумме вероятностей этих событий:

.

Пример 2.2.2. Подъемное устройство состоит из следующих основных узлов: троса А₁, полиспаста А₂, редуктора А₃, тормоза с электромагнитом А₄, электродвигателя подъемника А₅. Отказ хотя бы одного узла приводит к отказу всего подъемного устройства. За время t вероятность безотказной работы составила: узла А₁ - Р₁ = 0,90; А₂ - Р₂= 0,96; А₃ - Р₃ = 0,85; А₄ – Р₄ = 0,90; А₄ – Р₄ = 0,89;. Каждый из узлов, независимо от других, может в течении времени t выйти из строя. Найти вероятность безотказной работы подъемного устройства в целом.

Решение: Появление любого из этих событий вызывает отказ всей системы, поэтому

.

Пример 2.2.3. При проверке партии деталей 90% изделий были признаны годными (событие А). Из каждой сотни годных приборов 80% были высшего качества (событие В). Определите вероятность того, что выбранная нами деталь окажется высшего качества.

Решение: Из условия задачи можно сказать, что вероятность события А равна 0,90; вероятность события В – Р(А/В) = 0,80. Тогда вероятность того, что выбранная нами деталь окажется высшего качества равна:

.

2.3. Функции распределения плотности вероятности.

Известно около 160 законов распределения плотности вероятности. На практике используются некоторые наиболее распространенные: биноминальное, Пуассона, экспоненциальное, нормальное, Вейбула, бета-распределение. При оценке параметров совокупности данных используются распределения Стьюдента (t-распределение), ²-распределение и F-распределение.

Биноминальное распределение имеет место в том случае, когда вероятность появления события (х) в (n) независимых опытах постоянна и равна (Р). Вероятности появления (х) событий в серии из (n) испытаний соответствует функция распределения:

здесь р - вероятность отказа;

q=1-р вероятность появления события.

Среднее значение  = np, среднеквадратичное отклонение .

Если р очень мало, например р = 0,02 и q  1, а  гораздо больше р, биноминальное распределение трансформируется к виду:

Эта формула носит название распределение Пуассона, оно характерно для числа появления редких событий дискретной случайной величины (например, отказов систем).

Если р велико, и соответственно np тоже велико, например р  0,5, а np  5, биноминальное распределение может быть представлено в виде:

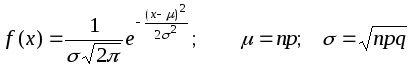
Данная формула носит название нормального или гауссова распределения. График нормального распределения приведен на рис.2.2.

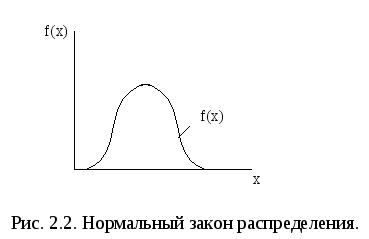
Нормальное распределение является одним из наиболее распространенных в технике.

Для экспоненциального закона распределения характерна формула:

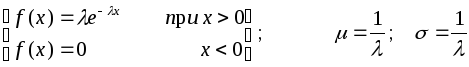
 - некоторый параметр, характеризующий частоту отказов.

График экспоненциального распределения приведен на рис. 2.3.

Экспоненциальное распределение характерно для отказов элементов технических систем.

При решении практических задач нередко достаточно определить только некоторые числовые характеристики, например, математическое ожидание, дисперсию и среднее квадратичное отклонение.

Математическое ожидание дискретных случайных величин определяется по формуле:

.

Математическое ожидание непрерывных случайных величин определяется по формуле:

.

Математическое ожидание величины при биноминальном распределении определяется по формуле:

.

Дисперсия дискретных случайных величин определяется по формуле:

.

Дисперсия непрерывных случайных величин определяется по формуле:

.

Дисперсия величины при биноминальном распределении определяется по формуле:

.

Среднее квадратичное отклонение равно:

.

Пример 2.3.1. При обследовании 100 разбрызгивателей обнаружено Х бракованных изделий. Вероятность появления бракованного изделия – 0,01. Определите математическое ожидание, дисперсию и среднее квадратичное отклонение числа бракованных разбрызгивателей.

Решение: Закон распределения для данной системы – биноминальный. Математическое ожидание такой системы равно:

Дисперсия:

Среднее квадратичное отклонение:

Пример 2.3.2. Проведено 100 независимых испытаний. Вероятность того, что появится некоторое событие m равно 0,05. Определите математическое ожидание появления события m.

Решение: Вероятность появления события m равна 0,05, а вероятность того, что это событие не появится – q = 1-р = 1-0,05 = 0,95. Тогда математическое ожидание появления события m равно:

,

т.е. при вероятности поломки 0,05, математическое ожидание срока службы составляет 20 лет.