
- •1.3 Стадии ндс
- •2).Две группы предельных состояний
- •3. Классификация нагрузок. Нормативные и расчетные нагрузки
- •4. Метод расчета железобетонных конструкций по предельным состояниям
- •5. Степень ответственности зданий и сооружений
- •6.Нормативные и расчетные сопротивления бетона.
- •8. Три категории требований к трещиностойкости железобетонных конструкций
- •9.Основные положения расчета по первой и второй группам предельных состояний
- •10.Общий способ расчета прочности элементов по методу предельных состояний
- •11. Граничная высота сжатой зоны
- •11.Конструктивные особенности однопролетных и многопролетных плит
- •12. Конструктивные особенности балок
- •13.Расчет прочности по нормальным сечениям элементов прямоугольного профиля с одиночным армированием
- •14. Расчет прочности по нормальным сечениям элементов прямоугольного профиля с двойным армированием
- •15.Установление случая расчета изгибаемых элементов таврового профиля
- •16.Расчет прочности по нормальным сечениям изгибаемых элементов таврового сечения (1-ый случай)
- •17.Расчет прочности по нормальным сечениям изгибаемых элементов таврового сечения (2-ой случай)
- •18. Расчет прочности изгибаемых элементов по наклонным сечениям на действие поперечной силы
- •19. Конструктивные особенности сжатых элементов
- •20. Расчет прочности условно центрально сжатых элементов
- •21.Конструктивные особенности растянутых элементов
- •22. Расчет прочности центрально-растянутых элементов
- •23.Классификация плоских перекрытий
- •24. Компоновка конструктивной схемы перекрытия
- •25.Формы поперечного сечения и расчетные пролеты плит балочных и сборных перекрытий
- •30.Конструирование отдельных фундаментов
- •31. Расчёт центрально нагруженного фундамента
12. Конструктивные особенности балок
Одним из наиболее распространенных элементов стальных конструкций является балка или элемент, работающий на изгиб.
По статической схеме различают однопролетные (разрезные), многопролетные (неразрезные) и консольные балки. Разрезные балки проще неразрезных в изготовлении и монтаже, нечувствительны к различным осадкам опор, но уступают последним по расходу металла на 10...12%. Неразрезные балки разумно применять при надежных основаниях, когда нет опасности перегрузки балок вследствие резкой разницы в осадке опор. Консольные балки могут быть как разрезными, так и многопролетными. Консоли разгружают пролетные сечения балок и тем самым повышают экономические показатели последних.
По типу сечения балки могут быть прокатными либо составными: сварными, клепаными или болтовыми. В строительстве наиболее часто применяют балки двутаврового сечения. Они удобны в компоновке, технологичны и экономичны по расходу металла.
13.Расчет прочности по нормальным сечениям элементов прямоугольного профиля с одиночным армированием
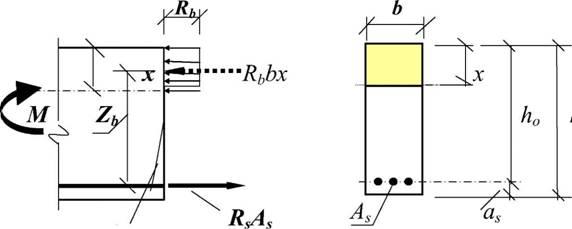
Прочность изгибаемых железобетонных элементов любого симметричного профиля по нормальным сечениям, согласно первой группе предельных состояний, рассчитывают по III стадии напряженно-деформированного состояния. В расчетной схеме усилий принимают, что на элемент действует изгибающий момент М, вычисляемый от расчетных значений нагрузок, а в арматуре и бетоне действуют усилия, соответствующие напряжениям, равным расчетным сопротивлениям.
 Расчетная схема
усилий в нормальном сечении изгибаемого
железобетонного элемента прямоугольного
профиля при расчете прочности
Расчетная схема
усилий в нормальном сечении изгибаемого
железобетонного элемента прямоугольного
профиля при расчете прочности
В целом при выводе расчетных зависимостей принимаются следующие расчетные предпосылки:
в бетоне сжатой зоны криволинейную эпюру напряжений заменяют прямоугольной, что несущественно влияет на результаты расчета; величина напряжений в сжатом бетоне принимается равной Rb - расчетному сопротивлению бетона при сжатии;
работой растянутого бетона пренебрегают полностью, что соответствует стадии разрушения конструкции;
все растяжение в стадии Ш воспринимает арматура; при этом напряжения в растянутой арматуре принимают равными расчетному сопротивлению стали RV;
в основу расчета принят первый случай разрушения, как для нормально армированного сечения, то есть принято выполняющимся условие :
Здесь x - относительная высота сжатого бетона R
Равнодействующие нормальных напряжений в арматуре и бетоне равны, соответственно:
В соответствии с общими условиями МПС прочность элемента достаточна, если внешний расчетный изгибающий момент М не превосходит расчетной несущей способности сечения выраженной в виде обратно направленного момента внутренних сил Mper, то для определения расчетного выражения для Mper используем закон равновесия моментов в сечении, известный из «Строительной механики»: 6ML = 0.
Если указанный закон записать относительно оси, проходящей через точку приложения равнодействующей усилий во всей растянутой арматуре, то условие прочности выразится неравенством.
Полученное выражение и будет искомым условием прочности нормального сечения изгибаемого железобетонного элемента с одиночным армированием.
Если применить закон равновесия моментов относительно центра тяжести сжатой зоны бетона (то есть точки приложения равнодействующего усилия в сжатом бетоне), то условие прочности выразится неравенством другого вида:
Здесь Zb = h0 - 0.5x представляет собой плечо внутренней пары сил (см. рис.9).
Для практического применения формулы прочности (1) либо (2) необходимо вначале определить высоту сжатого бетона X. Для решения этой проблемы удобно воспользоваться условием равновесия продольных сил в сечении изгибаемого элемента
Только в том случае, когда указанное условие выполнено, найденное значение х может быть подставлено в условие прочности (1) либо (2), приведенные выше, для проверки прочности сечения.
Если условие прочности выполнено, прочность обеспечена, то есть элемент не разрушится при действие на сечение внешнего момента M.
В противном случае элемент разрушится при действии на сечение момента M.
Следует обратить внимание, что проверяют лишь одно из условий прочности, так как они тождественны.
