3. Методика введения понятия вектора и изучения операций над векторами в курсе планиметрии.

1. Цели изучения этой темы.

1. Работы Г.Веселя, К.Ф.Гаусса по теории комплексных чисел установили связь между арифметическими операциями над комплексными числами и геометрическими операциями над векторами в двумерном пространстве – на плоскости.

2. В работах В.Гамильтона, Ф.Мебиуса понятие вектора нашло широкое применение при изучении свойств трехмерного и многомерного пространств.

3. В математике на векторной основе излагаются линейная алгебра, аналитическая и дифференциальная геометрия.

4. Вектор – понятие математическое, которое позволяет упростить рассмотрение некоторых вопросов, а также решение задач.

Основная цель – познакомить учащихся с элементами векторной алгебры и их применением для решения геометрических задач, сформировать умение производить операции над векторами.

2. В каких классах и сколько часов изучается.

1. В учебнике А.В.Погорелова векторы появляются в конце 8 класса. Дается : 8-15 часов.

2. В учебнике Л.С.Атанасяна изучаются в начале 9 класса (18ч)

3. В учебнике И.Ф. Шарыгина изучаются в 9 классе (16ч)

4. Характеристика основных подходов к изучению темы.

Существуют различные подходы к ведению этого понятия:

1. В учебнике А.В.Погорелова : «Направленный отрезок называется вектором ».

2. В учебнике Л.С. Атанасяна : «Отрезок, для которого указано, какой из его концов является началом, а какой - концом называется направленным отрезком или вектором»

3. Характеристика теоретического материала.

Содержание темы «Векторы» составляют следующие вопросы по учебнику А.В. Погорелова: «Перемещения. Векторы и способы их задания. Вектор как частный случай перемещения. Сложение векторов. Переместительность сложения векторов. Коллинеарные векторы. Сочетательность сложения векторов. Умножения вектора на число. Основные законы векторной алгебры. Векторные величины о физике. Композиция произвольных перемещений (последние два вопроса факультативно)».

По учебнику И.Ф.Шарыгина: декартовы координаты на плоскости. Уравнение линии. Векторы на плоскости. Скалярное произведение векторов. Координатный и векторный методы.

В учебнике Л.С.Атанасяна тема «Векторы»: Понятие вектора. Сложение и вычитание векторов. Умножение вектора на число. Применение векторов. Тема «Метод координат», в частности, содержит: Координаты вектора. Связь между координатами вектора и координатами его начала и конца.

По учебнику Л.С. Атанасяна:

- определение вектора, нулевой вектор, длина вектора

-равенство векторов, коллинеарные векторы

-откладывание вектора от данной точки

- сложение и вычитание векторов

- умножение вектора на число

- разложение вектора по двум неколлинеарным векторам

1. Теоремы, свойства, правила.

- свойства (законы) сложения векторов.

- теорема о разности векторов.

- правило параллелограмма.

- правило треугольника.

- операция над векторами (сложение ( вычитание) векторов, умножение вектора на число).

- разложение векторов по двум неколлинеарным векторам.

3. Математические методы.

1. Координатный метод.

2. Метод решения различных геометрических задач:

- применение векторов при доказательстве теорем.

- методика решения геометрических задач с помощью векторов.

4. Характеристика задачного материала

Для формирования понятия непосредственного применение изученных утверждений: 10

Для закрепления алгоритмов: 6

Для раскрытия и непосредственного применение математических методов: 3 доказательство некоторых теорем с помощью вектора, решение геометрических задач.

На постановку задачи и ее принятия: 4

На реализацию поиска решения: 18

На реализацию плана: 3

На критическое осмысление результатов решения: 2

По учебнику Л.С.Атанасяна вначале для формирования введенных понятий даются практические задания, затем вопросы и задачи. Основное внимание уделяется операциям над векторами. Рассматривается применение векторов к решению задач, с помощью применение векторного метода при доказательстве теорем рассматривается пример доказательства теоремы о средней линии трапеции.

5. Методы обучения.

На уроке ИНМ (иллюстративно- наглядный метод): наглядное ( показ материала).

На уроке закрепление: репродуктивные (решения задач)

На уроке проверки ЗУН: контрольно – оценочные (методы контроля и самоконтроля).

На уроке систематизации и обобщения: практические (упражнения, лабораторные работы, практикум, обобщающие игры по всем пройденным темам.).

В процессе изучения данной темы основное внимание уделяется выполнению операций над векторами в геометрической форме, так как этот материал используется при изучении физики. Поэтому полезно воспользоваться знаниями учащихся о векторных величинах, полученных на уроках физики, и это также может служить для мотивированного введения на предметной основе основных понятий темы. Понятие равенства векторов вводится на интуитивной основе.

Теперь рассмотрим изучение операции над векторами: сумма векторов определяется с помощью понятия композиции параллельных переносов, причем композиция понимается в том смысле, что эти переносы выполняются последовательно один за другим.

Ознакомление школьников с понятием суммы векторов можно начать с практической работы:

1. Постройте два отрезка, изображающие два несонаправленных и не противоположно направленных векторов

2. Отметьте на плоскости произвольную точку А.

3. Постройте точку В, являющуюся образом точку А при преобразовании .

4. Постройте точку С, являющуюся образом точки В , при преобразовании

В С

А

После выполнения этого задания перед учащимися можно поставить вопрос: можно ли каким-либо одним отображением плоскости на себя заменить два отображения , выполненных последовательно, переводя при этом точку А в точку С?

Ответ: , т. к. пара точек А и С определяет единственный вектор. Указать что, возможность такой замены 2-х последовательно проведенных //-х переносов может быть доказана (это доказательство в учебнике дано петитом).

Вектор - называют суммой векторов ; ввести обозначение и дать определение суммы векторов: операция нахождения суммы векторов называется сложением.

Сочетательность сложения векторов: и закон «поглощения нулевого вектора»: изучается аналогично (переместительный закон).

Изучение новой операции над векторами – умножение вектора на число – можно начать со следующих заданий:

1. Построить вектор представляющий сумму

АВ =a + a ; CD = a + a + a

В процессе выполнения этого задания выяснить с учащимся следующее:

1. данный и построенный векторы являются сонаправленными (имеют одно и то же направление).

2. длина построенного вектора /АВ/ равна произведению длины вектора а на число 2. Результат операции выразить в записи:

А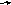В = 2 · а

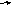
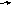2. Рассматривая задачу построения вектора, противоположного данному векторуb, не трудно мотивировать учащимся, что вектор b целесообразно рассматривать как вектора b на число -1, т. е. –b = (-1) · b…

Потом датьопределение: произведение вектора а на число х и рассмотреть равенство /ха/ = /х/·/а/ (1), являющееся следствием этого определения.

Здесь учителю следует дать некоторые дополнительные пояснения к тексту учебника. Прежде всего следует подчеркнуть, что равенство (1) по существу выражается вторая часть определения умножения вектора а на число х.

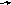
Следовательно:

• 0· а = 0 и х · 0 = 0 – нулевой вектор;

• если а = 0, то /а/ = /0/ = 0

• единичный вектор: е = 0Е, тогда для любого х можно изобразить геометрическим вектором хе .