
Алгебраические системы( 2 семестр,озо, спец. М). Варианты 1-10 Вариант 1
На множестве всех целых чисел Z задана бинарная операция по правилу x,yZ xyxy8x8y56. Докажите, что операция ассоциативна. Найдите нейтральный элемент для операции . Выполняется ли правило сокращения для операции ?
Докажите, что множество
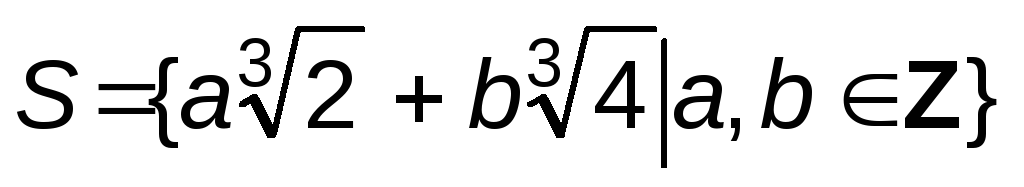 образует подгруппу аддитивной группы
действительных чисел <R,+>?
Будет ли S
подкольцом поля действительных чисел
R?
образует подгруппу аддитивной группы
действительных чисел <R,+>?
Будет ли S
подкольцом поля действительных чисел
R?. Решите уравнение AXB=C для подстановок 6-ой степени A=(123)(456), B=(12634) и C=(13)(2564). Найдите число инверсий и знаки подстановок A, B, C и X.
Докажите (методом математической индукции), что 7n30n1 делится на 36 при любых натуральных n.
Найдите x и y, считая их действительными числами: (16i)x(611i)y517i.
Решите уравнение z2(55i)z612i0.
Докажите, что множество
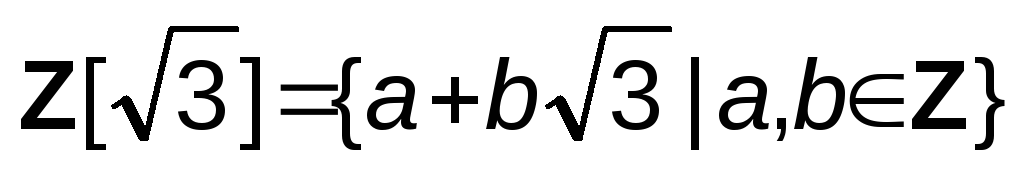 есть
подкольцо поля действительных чиселR.
Будет ли множество
есть
подкольцо поля действительных чиселR.
Будет ли множество
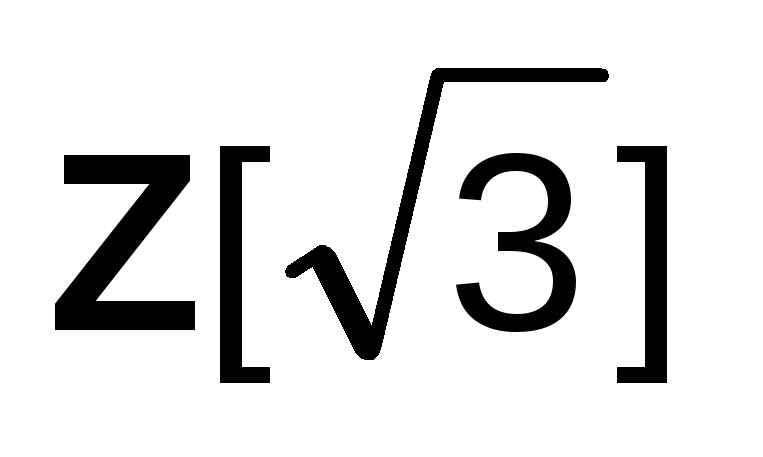 кольцом с единицей? Будет ли кольцо
кольцом с единицей? Будет ли кольцо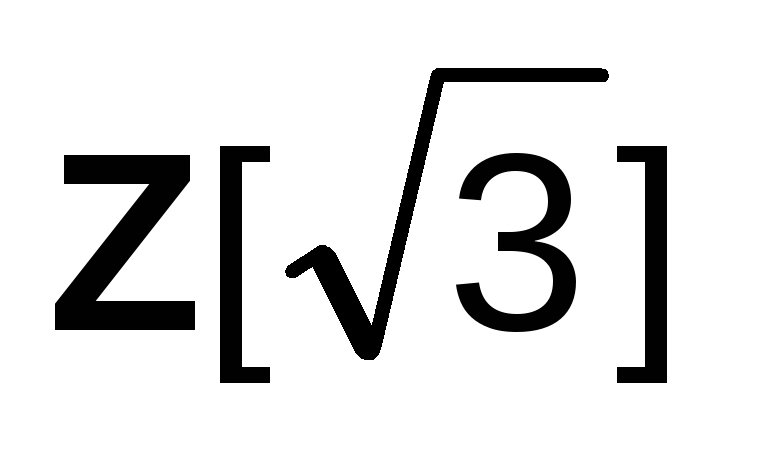 полем?
Будет ли кольцо
полем?
Будет ли кольцо
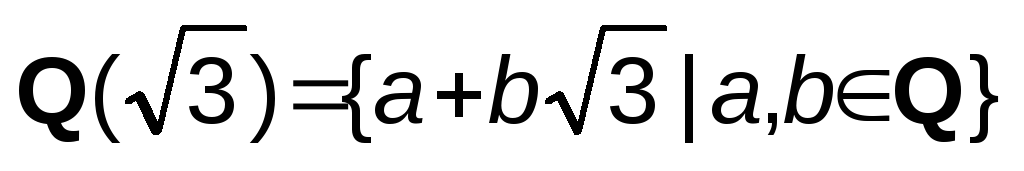 полем?
полем?Докажите, что кольцо
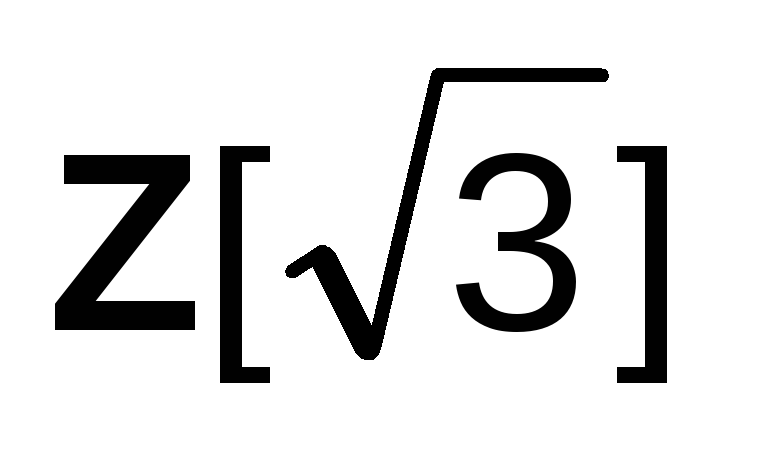 есть подкольцо кольца
есть подкольцо кольца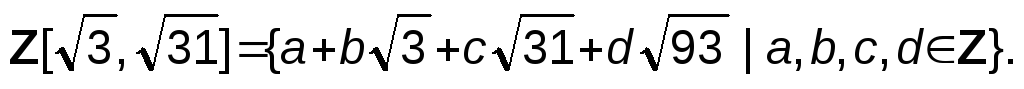
Докажите, что множество матриц
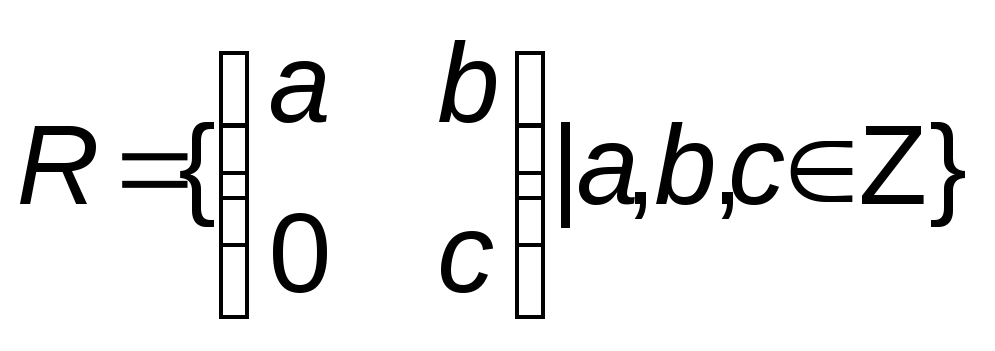 является кольцом. Зададим отображение
:RZ
по следующему правилу:
является кольцом. Зададим отображение
:RZ
по следующему правилу:
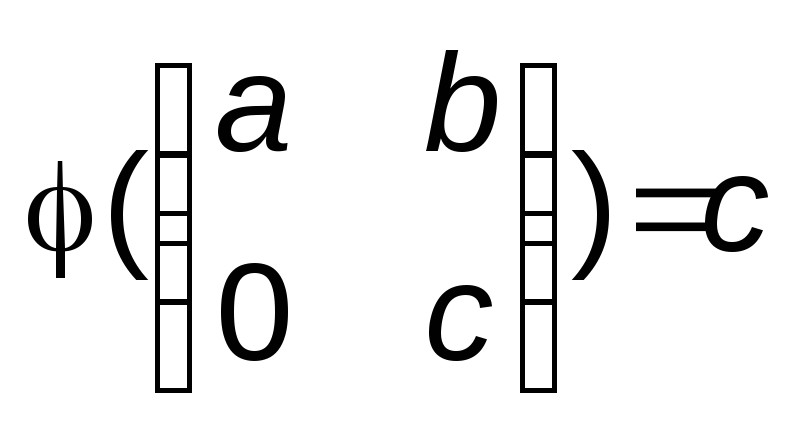 для всех a,b,cZ.
Докажите, что отображение
является гомоморфизмом колец. Найдите
ядро Ker.
для всех a,b,cZ.
Докажите, что отображение
является гомоморфизмом колец. Найдите
ядро Ker.
Вариант 2
На множестве всех целых чисел Z задана бинарная операция по правилу x,yZ xyxy7x7y42. Докажите, что операция ассоциативна. Найдите нейтральный элемент для операции . Выполняется ли правило сокращения для операции ?
Докажите, что множество
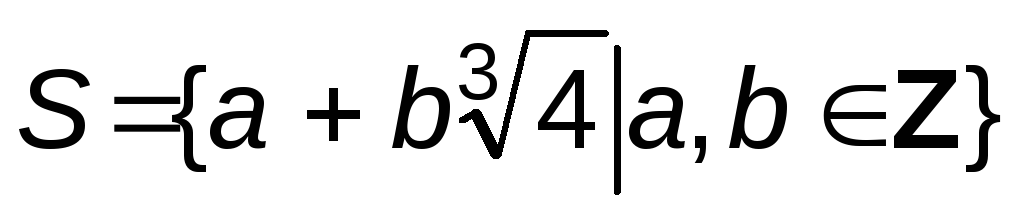 образует подгруппу аддитивной группы
действительных чисел (R,+)?
Будет ли S
подкольцом поля действительных чисел
R?
образует подгруппу аддитивной группы
действительных чисел (R,+)?
Будет ли S
подкольцом поля действительных чисел
R?Решите уравнение AXB=C для подстановок 6-ой степени A=(124)(356), B=(15236) и C=(14)(2536). Найдите число инверсий и знаки подстановок A, B, C и X.
Докажите (методом математической индукции), что 6n20n1 делится на 25 при любых натуральных n.
Найдите x и y, считая их действительными числами: (95i)x(72i)y127i.
Решите уравнение z2(4i)z3i0.
Докажите, что множество
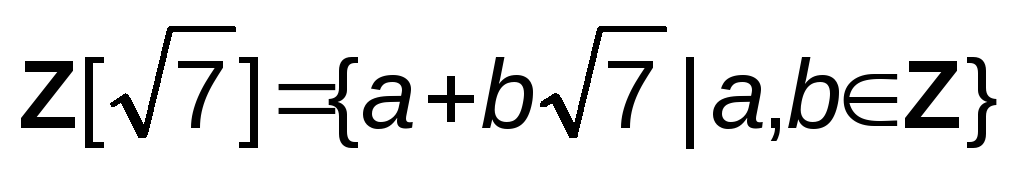 есть
подкольцо поля действительных чиселR.
Будет ли множество
есть
подкольцо поля действительных чиселR.
Будет ли множество
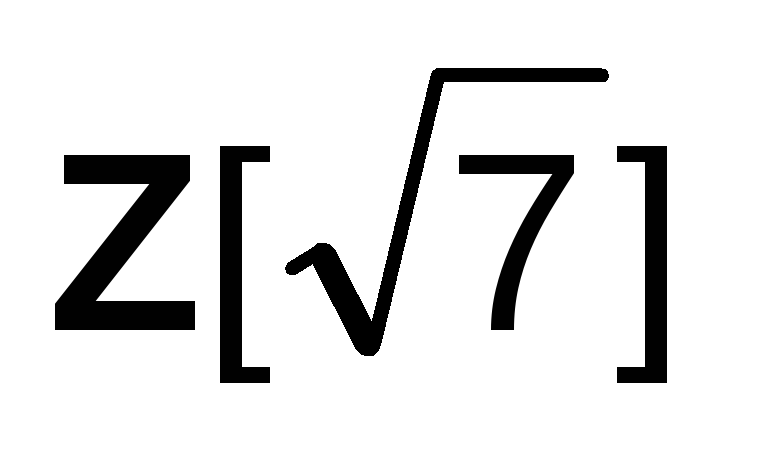 кольцом с единицей? Будет ли кольцо
кольцом с единицей? Будет ли кольцо полем?
Будет ли кольцо
полем?
Будет ли кольцо
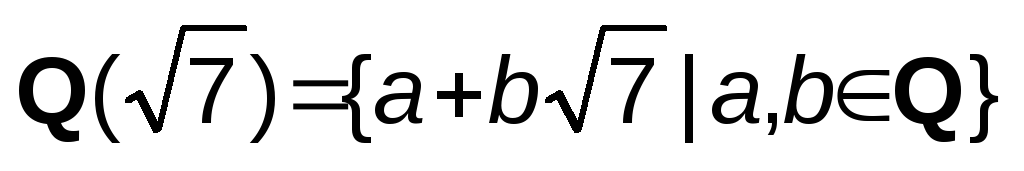 полем?
полем?Докажите, что кольцо
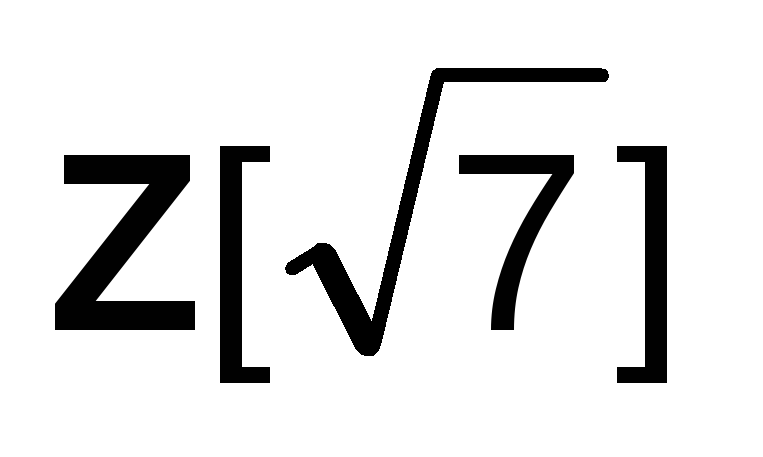 есть подкольцо кольца
есть подкольцо кольца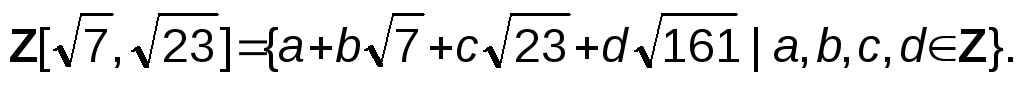
9.
Докажите, что множество матриц
![]() является кольцом. Зададим отображение
:RZ
по следующему правилу:
является кольцом. Зададим отображение
:RZ
по следующему правилу:
![]() для всех a,bZ.
Докажите, что отображение
является гомоморфизмом колец. Найдите
ядро Ker.
для всех a,bZ.
Докажите, что отображение
является гомоморфизмом колец. Найдите
ядро Ker.
Вариант 3
На множестве всех целых чисел Z задана бинарная операция по правилу x,yZ xyxy6x6y30. Докажите, что операция ассоциативна. Найдите нейтральный элемент для операции . Выполняется ли правило сокращения для операции ?
Докажите, что множество
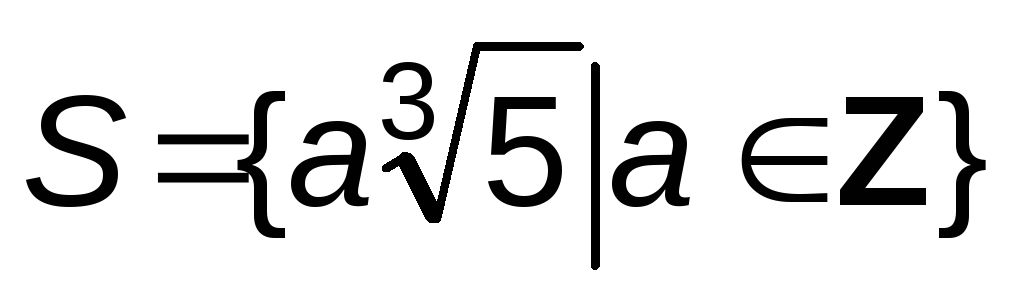 образует подгруппу аддитивной группы
действительных чисел (R,+)?
Будет ли S
подкольцом поля действительных чисел
R?
образует подгруппу аддитивной группы
действительных чисел (R,+)?
Будет ли S
подкольцом поля действительных чисел
R?Решите уравнение AXB=C для подстановок 6-ой степени A=(126)(354), B=(14526) и C=(15)(2364). Найдите число инверсий и знаки подстановок A, B, C и X.
Докажите (методом математической индукции), что 5n12n1 делится на 16 при любых натуральных n.
Найдите x и y, считая их действительными числами:(813i)x(511i)y38i.
Решите уравнение z2(32i)z24i0.
Докажите, что множество
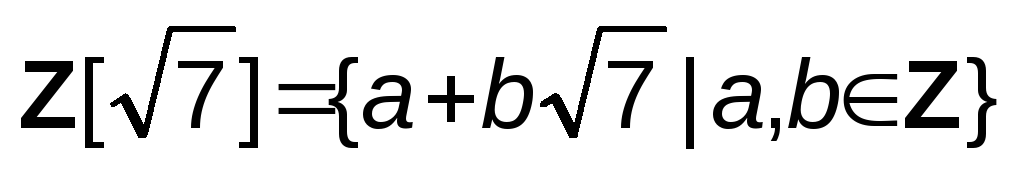 есть
подкольцо поля действительных чиселR.
Будет ли множество
есть
подкольцо поля действительных чиселR.
Будет ли множество
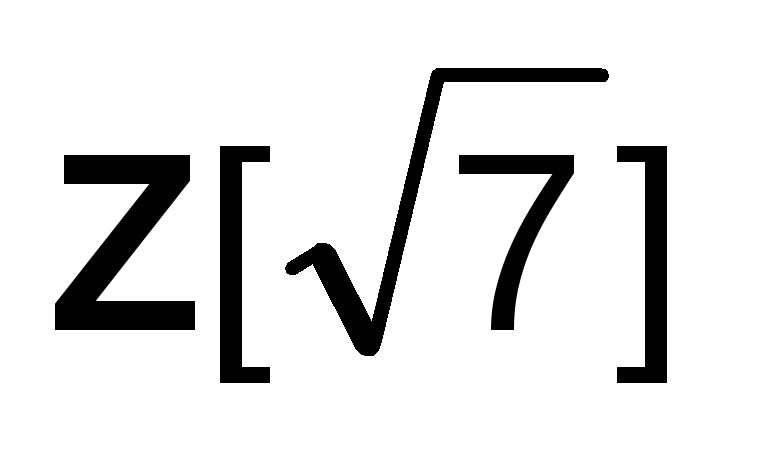 кольцом с единицей? Будет ли кольцо
кольцом с единицей? Будет ли кольцо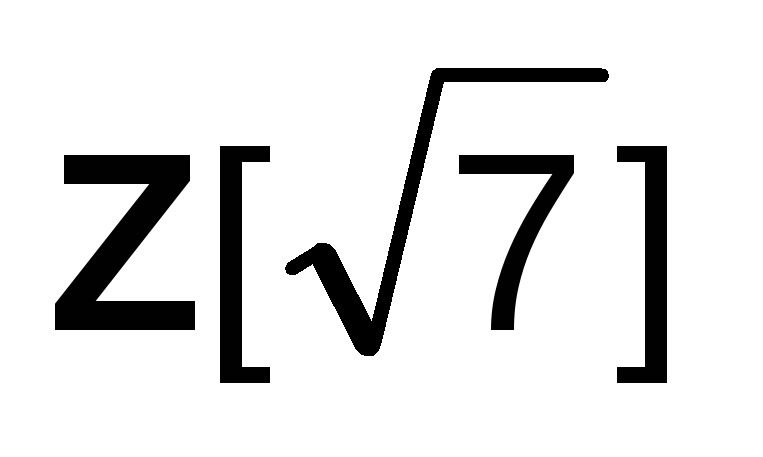 полем?
Будет ли кольцо
полем?
Будет ли кольцо
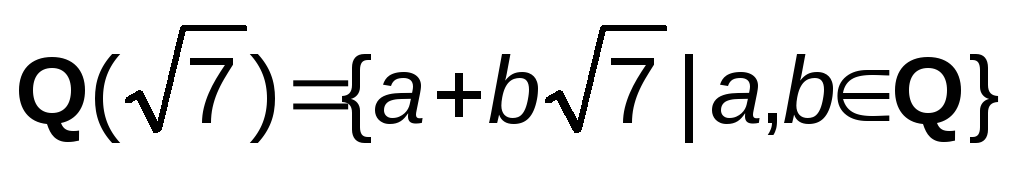 полем?
полем?Докажите, что кольцо
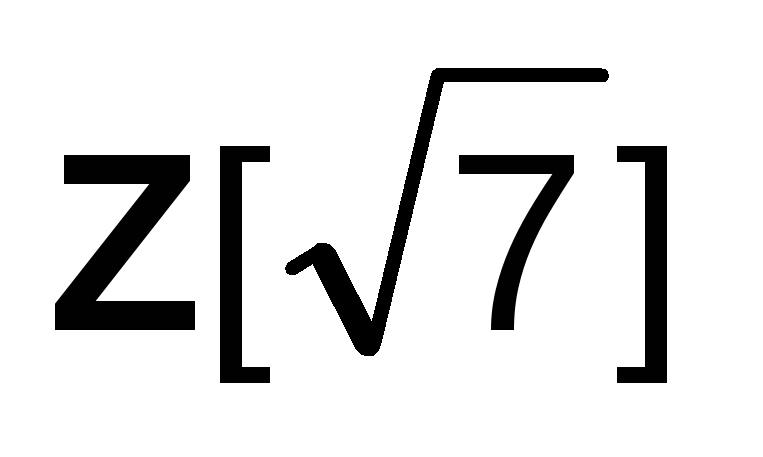 есть подкольцо кольца
есть подкольцо кольца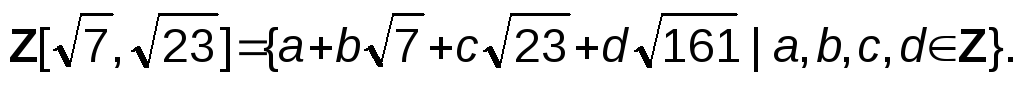
Докажите, что множество матриц
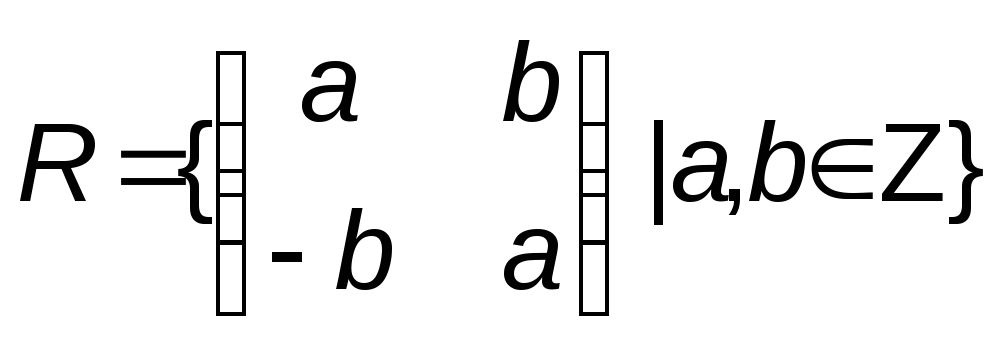 является кольцом. Зададим отображение
:RZ
по следующему правилу:
является кольцом. Зададим отображение
:RZ
по следующему правилу:
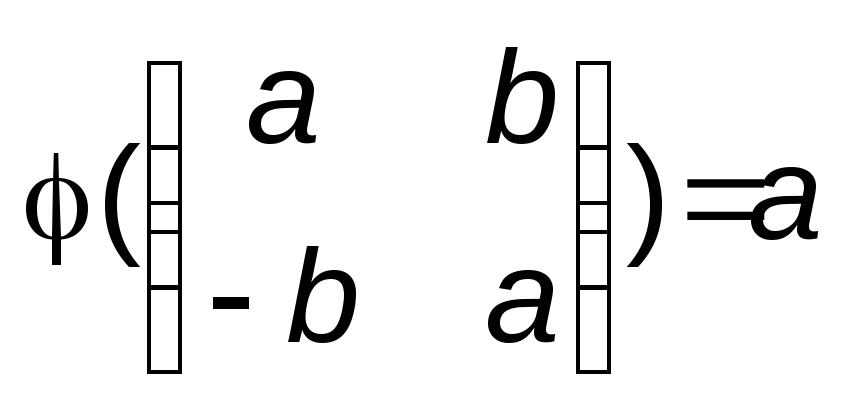 для всех a,bZ.
Докажите, что отображение
является гомоморфизмом колец. Найдите
ядро Ker.
для всех a,bZ.
Докажите, что отображение
является гомоморфизмом колец. Найдите
ядро Ker.
