Научные стремления 2012-1

где m0 – масса удобрений проходящих через барабан за 1 сек;a – абсолютная скорость схода удобрений с лопатки;

m0 Bтр Vтр H γ .

где Vтр – скорость движения подающего транспортера, м/с;

H – высота слоя удобрений на подающем транспортере, м; Втр – ширина подающего транспортера, м; γ – насыпная плотность удобрений, кг/м3.

Из формулы следует, что работа, необходимая для разгона произвольного комка удобрений до скорости выброса рабочим органом, имеющим радиальные лопатки, равна произведению массы этих удобрений на квадрат скорости наружных концов лопаток барабана. Тогда мощность, расходуемая на сообщение частицам необходимой кинетической энергии, определится по формуле:

1 - угол трения материала о лопасть.

Относительная скорость движения частиц по лопасти будет изменяться от нуля до максимума. Следовательно, для расчетов необходимо принимать максимальное значение для абсолютной скорости a .

Для перемещения частицы на край лопасти необходимо затратить энергию на сообщение ей соответствующей живой силы и преодоление сопротивления трения по лопасти. Чтобы определить мощность, расходуемую на преодоление этой силы, необходимо знать среднюю относительную скорость движения частиц по лопасти и силу трения частиц о лопасть. Сила

трения частицы удобрений о лопасть определяется выражением [2]: Fтр f 2 m a m g sin .

где - угловая скорость лопастного барабана, с-1;

f – коэффициент трения частицы по поверхности лопатки;

g– ускорение свободного падения, м/с2;

- угол поворота лопасти от линии горизонта в данный момент

времени.

Во время работы лопасти значение угла меняется от 0º до 90º и наоборот. Поэтому направление силы трения и ее значение переменного характера. Тогда мощность, расходуемая на преодоление сил трения удобрений о лопасть:

291

происходит порциями, а не сплошным непрерывным потоком, необходимо учитывать максимальное количество удобрений, которое может обрушиться на лопасть барабана. При этом масса обрушевшегося слоя удобрений будет равна [3, с.57]:

Анализ формулы показывает, что при линейном увеличении высоты слоя удобрений H масса m растет в квадратичной зависимости, а угол естественного откоса, который является случайной функцией времени, в

где M кр.в – крутящий момент вращающегося вокруг неподвижной оси

лопастного барабана.

В соответствии с теоремой о кинетической энергии вращающегося вокруг своей оси тела его крутящий момент находится из выражения:

где mб – масса лопастного барабана, кг.

Решив совместно уравнения (7) и (8) и подставив их в выражение (6), получим формулу для определения мощности на преодоление сопротивлений вращению лопастного барабана:

С учетом сказанного, формула полной мощности, необходимой для работы лопастного барабана будет иметь вид:

292

Из геометрических параметров на мощность лопастного барабана оказывает наибольшее влияние его диаметр. Как видно из формулы (10), с увеличением диаметра барабана мощность возрастает по квадратичной зависимости. При одних и тех же условиях работы с увеличением диаметра барабана мощность резко увеличивается. Из формулы также видно, что с увеличением частоты вращения при постоянном диаметре мощность возрастает непропорционально, так как она находится в квадратичной зависимости от угловой скорости вращения.

Выводы. Получена формула для определения мощности на привод лопастного барабана с учетом его конструктивно-кинематических параметров и физико механических свойств минеральных удобрений. При этом учтена мощность на придание частицам кинетической энергии, на преодоление сил трения удобрений о лопасть, на преодоление энергии удара и сопротивлений вращению барабана.

Литературные источники

1.Догановский, М.Г. К определению параметров роторных разбрасывающих механизмов / М.Г. Догановский, В.В. Рядных // Механизация и электрификация сельского хозяйства. – 1965. – №4. – С.8 – 11.

2.Бегун, П.П. Исследование движения минеральных удобрений по лопасти барабана выравнивающего устройства // П.П. Бегун// Механизация и электрификация сельского хозяйства: Межведомственный тематический сборник / Под общ. ред. В.Н.Дашкова. – Минск, 2012. – Вып. 46.

3.2Михеев, А.В. Исследование процесса подачи удобрений прутковым транспортером машин типа МВУ / А.В. Михеев // Технологические процессы и средства механизации применения минеральных удобрений. Сб. науч. тр.,Т –126.: – Москва, 1991. – 190 с.

4.Карбан, Г.Л. Снегоуборочные машины / Г.Л. Карбан // Уч. изд. /Министерство коммунального хозяйства РСФСР. – М.: 1962. –С.82 – 96.

Behun P.P. , Liakx A.A.

CALCULATION REQUIRED POWER ON A DRIVE BLADE DRUM OF THE EQUALIZER OF A STREAM OF MINERAL FERTILIZERS

Scientific and Practical Centre of the NAS of Belarus for agricultural mechanization

Summary

In article the design procedure required power on a drive blade a drum of the equalizer of a stream of mineral fertilizers is resulted.

293

УДК 3677.021.151

Бобровская И.Е.

ОБОСНОВАНИЕ РАЦИОНАЛЬНОГО РАСПОЛОЖЕНИЯ ДИСКОВ НА ВАЛАХ И СЛОЯ ЛЬНОТРЕСТЫ В СЛОЕФОРМИРУЮЩЕЙ МАШИНЕ

РУП "НПЦ НАН Беларуси по механизации сельского хозяйства", г. Минск

Среди прочих параметров, на процесс утонения слоя льнотресты в слоеформирующей машине существенное влияние оказывают расположение дисков на валах, ширина слоя льнотресты и расположение его перед слоеформирующей машиной.

Вранее выполненных теоретических работах [1, 2] исследовано влияние расстояния между дисками на валах на величину изменения угла дезориентации стеблей в слое, установлено влияние различий в сцепленности стеблей в комлевом и вершинном участках слоя на оптимальные значения расстояния между дисками на валу и расположения слоя [2]. Одним из критериев оценки работы машины предложен показатель – вероятная доля стеблей, которая успешно обрабатывается парой зубчатых дисков на одном валу (без разворота стеблей).

В[3, 4] приведены результаты исследований по оптимизации расположения слоя по отношению к зажимным транспортерам трепальной машины и влияния ширины слоя стеблей на этот параметр. Критерием для оптимизации параметров в исследованиях принят показатель – пригодность слоя к обработке трепанием, впервые предложенный А.М. Ипатовым [5], под которым понимается вероятная часть стеблей слоя льнотресты по массе, которая может быть зажата в обоих конвейерах трепальной машины.

Ранее выполненные исследования реализованы для машин с двумя линиями утонения и имеют теоретический характер.

Очевидно, что влияние на конечный результат таких факторов, как расстояние между дисками крайних линий утонения слоеформирующей машины dд (см); смещение оси слоя на входе в слоеформирующую машину от

осевой линии слоеформирующей машины (средней линии утонения) xо (см) в

машине с тремя утоняющими линиями отличается от исследованного. Поэтому целью данной работы являлось экспериментальное исследование влияния этих факторов на результаты работы слоеформирующей машины и их оптимизация.

В качестве параметра оптимизации был принят показатель пригодности слоя к обработке трепанием, Пт (доли единицы). Для его экспериментального

определения использовали несколько видоизмененный метод и оборудование (лабораторные зажимные колодки и гребень) для определения пригодности тресты [6, с. 66].

Исследования проводились на экспериментальном образце слоеформирующей машины МС-6,97 с тремя линиями утонения, в котором

294

была предусмотрена возможность изменения расстояния между крайними и средним диском каждого вала.

Для варьирования расположением слоя относительно зажимных конвейеров трепальной машины делали их привязку к дискам среднего ряда слоеформирующей машины. За линию отсчета принимали осевую линию слоя тресты, которую смещали относительно среднего ряда дисков в сторону комлевой и вершинной его частей.

Факторы, уровни и интервалы варьирования факторов приведены в таблице 1.

Таблица 1 – Уровни и интервалы варьирования факторов

но как фактор – является трудно управляемым, эксперименты по поиску оптимальных значений факторов проводили на тресте различной горстевой

длины ( Lг 1 60 см, Lг 2 70 см).

Эксперимент был поставлен по программе центрального композиционного ротатабельного планирования второго порядка [7].

В ходе эксперимента фрагмент слоя льнотресты, полученный путем размотки рулона, располагался на конвейерном столе слоеформирующей машины при сохранении его структуры и пропускался через механизм утонения экспериментального образца слоеформирующей машины при вращении рабочих органов (зубчатых дисков) в ручном режиме. Выходящий из слоеформирующей машины слой при сохранении его структуры размещался на столе, имеющем отметку, соответствующую оси зажимнотранспортирующего механизма первой секции трепальной машины. От слоя отбиралась проба шириной примерно 35 см, которая взвешивалась на весах (ВТНт-10М) и затем на участке, соответствующем отметке, зажималась в лабораторную колодку.

295

Рисунок 1. Прочес льнотресты

Зажатые в колодке стебли льнотресты прочесывали с помощью гребня (рисунок 1) со стороны комлевой части. Следует отметить, что при прочесе комлевой части наряду с удалением не попавших в зажим стеблей устранялась дезориентация в оставшихся стеблях, что соответствует явлениям, происходящим при трепании и не оказывает негативного влияния на результат эксперимента. После прочеса комлевой части слой зажимался второй колодкой, расположенной на расстоянии 17 см от первой со стороны вершинной части и также прочесывался. Учитывая, что при прочесе выделялось существенное количество костры, непосредственное взвешивание оставшихся стеблей и вычисление пригодности по принятой в [6, с.66] формуле привело бы к высокой погрешности. Поэтому из очеса выбирали целые стебли, их взвешивали, а экспериментальное значение пригодности рассчитывали по формуле

где Пт – пригодность слоя льнотресты к обработке трепанием; mст – масса стеблей в очесах, кг;

m0 – общая масса порции, кг.

Показатель пригодности вычисляли по (1) с точностью до 0,001 г, с последующим округлением до 0,01г.

В результате обработки опытных данных (проверки гипотезы воспроизводимости дисперсий по G-критерию Кохрена, значимости коэффициентов регрессии по t-критерию Стьюдента) получены модели зависимости параметра оптимизации от исследуемых факторов, которые в натуральных значениях переменных имеют вид:

где: Y1 – пригодность к обработке трепанием для слоя с Lг 1 60 см, Y2 – для слоя с Lг 2 70 см.

Проверка по F-критерию Фишера показала, что модели (2,3) адекватны результатам экспериментов. Графическое изображение поверхностей отклика и их сечений по результатам обработки экспериментальных данных, выполненных с помощью программы ''Statistica", представлено на рисунках

2,3.

296

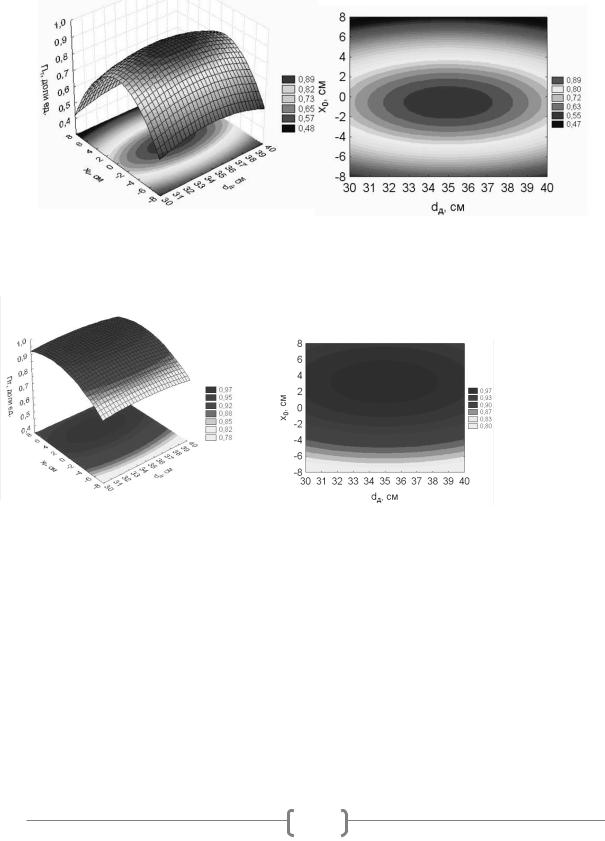
Поскольку интервалы рациональных значений dд для слоя с различной

горстевой длиной стеблей практически одинаковы, и в каждом случае оптимум функции достигается при dд 35,00 см, то целесообразно

устанавливать диски крайних линий утонения в слоеформирующей машине на данном расстоянии. Кроме того, в целях упрощения конструкции слоеформирующей машины можно отказаться от регулирования расстояния между дисками крайних линий утонения.

Рисунок 2. Поверхность отклика (а) и сечения поверхности отклика уравнения регрессии (б) для слоя с горстевой длиной 62 см

а) б)

Рисунок 3 – а) Поверхность отклика (а) и сечения поверхности отклика уравнения регрессии (б) для слоя с горстевой длиной 71 см

Таким образом, в результате выполненного двухфакторного эксперимента получены математические модели зависимостей пригодности слоя льнотресты с различной длиной стеблей к трепанию от расположения зубчатых дисков на валах и расположения слоя на конвейерном столе слоеформирующей машины . По полученным зависимостям определено оптимальное значение расстояний между зубчатыми дисками на валах слоеформирующей машины. Показана необходимость смещения слоя льнотресты перед слоеутонением при изменении длины стеблей льнотресты.

297

УДК 533.6.011.6

Герасимович Л.С., Косько А.Н

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПРОЦЕССА ТЕПЛООБМЕНА ЖИВОТНЫХ С СИСТЕМОЙ ИНФРАКРАСНОГО ОБОГРЕВА И РАСПОЗНАВАНИЕМ ОБРАЗОВ

Белорусский Государственный Аграрный Технический Университет, Минск

Введение. Животноводство является ведущей отраслью сельского хозяйства Республики Беларусь. Применение интенсивных способов содержания животных предъявляет повышенные требования к микроклимату животноводческих помещений. Значительное влияние на экономический эффект оказывает температурно-влажностный режим в помещении. Отсюда следует задача определения оптимальных условий содержания животных и контроля над микроклиматом в помещении. Трудность представляет теоретическое обоснование решения данной проблемы.

Основная часть. За основу для построения математической модели (ММ) процесса теплообмена (ТО) животных с системой инфракрасного обогрева примем следующие данные:

1.ТО происходит в ограниченном в пространстве помещении с заранее известными геометрическими параметрами;

2.Известно количество животных, участвующих в ТО n. Также известна средняя масса одного животного в данный период времени m , кг. В

общем случае данная величина суть функция многих параметров. Однако достаточно отметить, что масса есть функция от времени, т.е. m m(t);

3.Известны зоотехнические требования к температуре окружающей среды и материалам теплоотдающей поверхности ИК-облучателей.

Положим, что имеет место распределение массы по площади пола

облучатель отсутствует.

В общем случае распределение массы по площади не может быть

Можно доказать, что ρm суть случайная величина, причем подчиняется

она нормальному закону распределения. Действительно, согласно центральной предельной теореме, в случае, когда результат измерения (наблюдения) складывается под действием многих независимых причин, причем каждая из них вносит лишь малый вклад, а совокупный итог определяется аддитивно, т.е. путем сложения, то распределение результата измерения (наблюдения) близко к нормальному распределению. В данном случае количество помех велико, а каждый в отдельности их вклад невелик,

299

следовательно, можно утверждать, что распределение массы животных по площади подчиняется нормальному закону распределения.

Из опытных данных следует, что распределение животных по площади в отсутствии возмущающих воздействий будет практически равномерным. Это можно обосновать и теоретически, используя правило «трех сигм».

Теперь рассмотрим поведение функции (1) при наличии возмущающего воздействия. Данное воздействие осуществляется ИК-облучателем. За характеристику данного воздействия примем интенсивность теплового потока облучателя qucm .

В данном случае справедливо, что

Очевидно, что при условиях, которые благоприятны и приемлемы для животных, вне зависимости от того, есть ли внешнее воздействие, распределение массы по площади пола будет равномерным. Если же условия содержания, важнейшим критерием которых является температура внутреннего воздуха, не благоприятны для животных, то распределение массы по площади пола скорее всего равномерным не будет. Это легко объяснить. Согласно опытным данным, в случае, когда температура в помещении ниже благоприятной, животные в большей степени располагаются по площади пятна от облучателя. Когда же температура выше благоприятной, то животные располагаются в большей степени вне пятна от облучателя.

[qmin , qmax ] [o, qnp ] . Рассмотрим три возможных случая.

1.При qucm qmin животные будут располагаться в большей степени

по площади пятна от облучателя, так как температура в помещении будет пониженной.

2. При qucm [qmin , qmax ] животные будут располагаться по площади пола равномерно.

3.При qucm qmax животные будут располагаться в большей степени

вне площади пятна от облучателя.

Можно сделать вывод, что автоматизировать процесс климат контроля в животноводческом помещении можно анализируя поведение животных, что в данном случае описывается функцией (3).

Для такого метода контроля целесообразно применить систему видеонаблюдения и математическую теорию распознавания образов. Осуществить это можно следующим образом. Камера, подключенная к компьютеру, отслеживает перемещение животных по площади пола. Изображение, полученное камерой, обрабатывается программой распознавания образов. В зависимости от того, как распределена масса по площади, регулируется интенсивность теплового потока излучателя.

300