Дымков Лекции

Первичными понятиями в ТВ являются:

случайное событие и вероятность.

Случайным событием (возможным событием или просто событием) называется любой факт, который в результате испытания (эксперимента) может произойти или не произойти.

Под экспериментом понимается выполнение некоторого комплекса условий G , в которых наблюдается то или иное явление или факт.

Примеры случайного эксперимента: бросание монеты, бросание игральной кости, проведение лотереи, азартные игры, стрельба по цели, поступление звонков на телефонную станцию и т.п.

Событие—это не какое-то происшествие, а всего лишь

возможный исход, результат испытания (опыта,

эксперимента)

Различные результаты эксперимента называют

исходами.

Определение 1. Множество всех взаимоисключающих исходов эксперимента называется пространством элементарных событий. Взаимоисключающие исходы – это те, которые не могут наступить одновременно.

Пространство элементарных событий будем обозначать буквой Ω, а его исходы – буквой ω.

Пример Выпадение на игральной кости: одного очка

ω1,….., выпадение шести очков ω6 . Это элементарные события и их уже нельзя разбить на более мелкие.

На практике интересуют события неэлементарные.

Определение2. Произвольное подмножество из пространства элементарных событий называется

событием.

Событие может состоять из одного или нескольких элементарных событий, а также состоять из счетного или несчетного числа элементарных событий.

События обозначают обычно буквами: А, В, С…

Событие Ω, состоящее из всех исходов эксперимента, называется достоверным событием. Оно обязательно происходит, так как эксперимент всегда заканчивается каким-нибудь исходом.

Пустое множество исходов эксперимента называется невозможным событием и обозначается символом ø.

По-другому, невозможное событие—событие, которое никогда не произойдет в данном эксперименте

либо они произошли одновременно, т.е. произошло хотя бы одно из событий А или В.

Определение 4. Произведением двух событий А и В

(обозначается АВ или AIB) называется событие, состоящее из тех исходов, которые входят как в А, так и в В. Иными словами, АВ означает событие, при котором события А и В наступают одновременно.

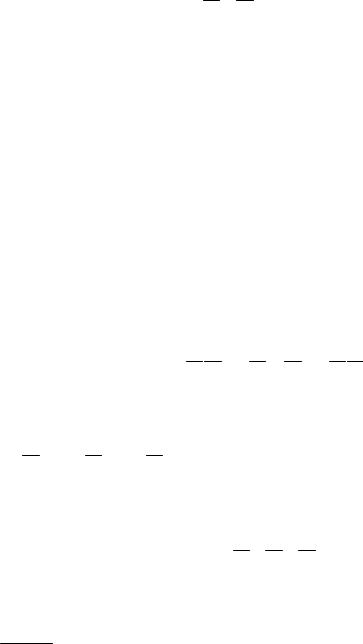
Если события изобразить на плоскости, то результат определенных операций над событиями выглядит так:

Определение6. Противоположным (дополнительным)

для события А (обозначается A) называется событие, состоящее из всех исходов, которые не входят в А. Наступление события A означает просто, что событие А не наступило.

Определение7. События А и В называются несовместными, если нет исходов, входящих как в А, так и в В, т.е. если АВ = ø. (По-другому, события несовместны, если появление одного исключат наступление другого)

Определение 8. Говорят, что событие А содержится в

событии В (обозначается A B), если все исходы события А входят в событие В.

Свойства операций над событиями:

1) A + B = A + B; 2) AB = BA; 3) A + A = Ω; 4) A Ω = A; 5) AB A; 6) AA = ø;

Пример 1. Два шахматиста играют подряд две партии. Под исходом опыта будем понимать выигрыш одного из них в i-ой партии или ничью. Построить пространство Ω элементарных исходов.

Решение. Обозначим события: Ai −в i-ой партии выиграл 1-ый игрок, Bi −2-ой игрок, Ci − ничья.

Тогда возможные исходы игры:

-обе партии выиграл первый игрок – A1 A2;

-обе партии выиграл второй игрок – B1 B2 ;

-обе партии закончились вничью – C1 C2 ;

-в первой партии выиграл первый игрок, во второй выиграл второй игрок – A1B2;

-в первой выигрыш 1-го игрока, во второй – ничья

A1C2;

- в первой партии победа игрока 2, во второй – первого

B1A2;

- в первой – победа второго игрока, во второй – ничья

B1C2;

- в первой – ничья, во второй – победа первого игрока –

C1A2;

- в первой – ничья, во второй – победа второго игрока –

C1B2.

Ответ:

Ù = { A1 A2, B1 B2 , C1 C2 , A1B2, A1C2, B1A2, B1C2, C1A2, C1B2 }.

произошли, тогда событие: произошло только А можно записать в виде: A B C .

2)произошло А и В, но С не произошло;

A B C

3)все три события произошли;

A B C

4)произошло, по крайней мере, одно из событий;

А+ В + С.

5)произошло, по крайней мере, два события;

АВ + АС + ВС.

6)произошло одно и только одно событие;

ABC + ABC + ABC

7)произошло два и только два события;

ABC + ABC + ABC, или АВ + АС + ВС – АВС. 8)ни одно событие не произошло;

A B C

9)произошло не более двух событий.

ABC , т.е. три события одновременно не произошли.

Основные правила комбинаторики.

1. Правило суммы.

Если два действия взаимо исключают друг друга, причем одно из них можно выполнить m способами, а другое – n способами, то выполнить одно любое из этих действий

можно N=n + m способами.

2. Правило умножения.

Пусть требуется выполнить одно за другим какие-то k действий. Если первое действие можно выполнить n1способами, после этого второе действие можно осуществить n2способами и т.д. и, наконец, после осуществления (k −1)-го действия, k-ое можно выполнить nk способами, то все k действий вместе могут быть выполнены N=n1 n2 n3 K nk способами.

Эти правила дают удобные универсальные методы решения многих комбинаторных задач.

Пример. Три человека независимо друг от друга решили поместить свои вклады в банк. Банков всего 8.

Тогда общее число способов выбора равно

N = 8 8 8 = 83

Пусть имеется множество Un, состоящее из n элементов.

Перестановкой из n элементов называется заданный порядок во множестве Un.

Примеры перестановок:

1)распределение n различных должностей среди n человек;

2)расположение n различных предметов в одном ряду.

Число перестановок обозначается Pn (читается “Р из n”).

Чтобы вывести формулу числа перестановок, представим себе n ячеек, пронумерованных числами 1,2,...n. Все перестановки будем образовывать, располагая элементы Un в этих ячейках. В первую ячейку можно занести

любой из n элементов (иначе: первую ячейку можно заполнить n различными способами). Заполнив первую ячейку, можно найти n–1 вариантов заполнения второй ячейки. Таким образом, существует n(n–1) вариантов заполнения двух первых ячеек. При заполнении первых двух ячеек можно найти n–2 варианта заполнения третьей ячейки, откуда получается, что три ячейки можно заполнить n(n-1)(n-2) способами. Продолжая этот

процесс, получим, что число способов заполнения n ячеек равно n(n −1)(n − 2)...3 2 1. Отсюда

Pn = n(n – 1)(n – 2)... 3 2 1=n! (1!=1; 0!=1)

Пример. Сколько существует вариантов замещения 5-ти различных вакантных должностей 5-ю кандидатами?

5!= 5 4 3 2 =120 .

Число сочетаний из n элементов по k элементов обозначается Cnk (читается "C из n по k").

Пример. Сколько существует вариантов выбора 6-ти человек из 15 кандидатов для назначения на работу в одинаковых должностях?

Свойство числа сочетаний

Cnm =Cnn−m

Замечание !!. Во всех вышеприведенных формулах предполагалось, что элементы выбирались без их возвращения

(говорят еще выборка без повторения).

Например, число размещений с повторяющимися из n

Пример. Для запирания сейфов и автоматических камер хранения применяют секретные замки, которые открываются лишь тогда, когда набрано некоторое «тайное слово». Пусть на диск нанесено 12 букв, а секретное слово состоит из 5 букв. Сколько неудачных попыток может быть сделано человеком, не знающим секретного слова?

Решение. Общее число возможных комбинаций есть

N = A125 =125 = 248832.

Ответ: 248831.