Типовые законы распределения
Для дискретных величин:
Биномиальный закон распределения
Проводим серию испытаний. В каждом из испытаний возможно наступление\ ненаступление события А. Причем вероятность наступления везде равна. Нас интересует вероятность того, что в серии из n испытаний наступит k успехов (наступление события).
Рассмотрим случайную
величину X – число появлений события A
в этих испытаниях. Случайная величина
X принимает значения 0,1,2,…n с вероятностями,
вычисленными по формуле Бернулли:
,
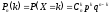гдеp(n)=k,
0<k<n,
q-вероятность
неуспеха.
Дискретная случайная величина X имеет биноминальное распределение, если ее возможные значения 0, 1, 2, …n, а соответствующие им вероятности рассчитываются по формуле Бернулли.
Случайная величина, распределенная по биномиальному закону, имеет математическое ожидание МХ=np, а дисперсию DX=npq.
Недостатком формулы Бернулли является то, что при больших значениях n пользоваться ей сложно, в таких случаях используют локальную теорему Лапласа.
Пример 1. Из учеников класса 40 % являются отличниками. Случайным образом выбрано 3 ученика. Составить закон распределения числа отличников из выбранных троих. Найти дисперсию и математическое ожидание.
Случайная
величина Х –
число отличников из выбранных троих.
В n=3 независимых
испытаниях вероятность того, что ученик
является отличником, равна p=0,4.
Соответственно, вероятность того, что
ученик не является отличником q=0,6.
Тогда биномиальный закон распределения
имеет вид:
|
xi |
0 |
1 |
2 |
3 |
|
pi |
0,216 |
0,432 |
0,288 |
0,064 |
По формуле Бернулли:
P(X=0) = 0,216
P(X=1) = 0,432
P(X=2) =0,288
P(X=3) =0,064
P = 0,216+0,432+0,288+0,064 = 1
M(X) =3*0,4=1,2
D(X) = 3*0,4*0,6=0,72
Распределение Пуассона
Распределение Пуассона имеет место, когда закон распределения случайной величины определяется следующим образом:
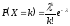,где
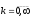и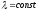
и равно np.
Данная формула используется в тех случаях, когда n велико, а p мало.
Для дискретных
случайных величин, распределенных по
закону Пуассона, МХ=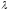
,DX=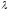
.
Пример 2. Станок изготавливает за смену 100000 деталей. Вероятность изготовления бракованной детали p=0,0001. Найти вероятность того, что за смену будет изготовлено 5 бракованных деталей. Найти математическое ожидание и дисперсию.
Решение: n = 100000, p = 0,0001, k = 5. Найдем λ: λ = np = 10.
По формуле Пуассона вероятность равна:
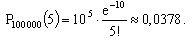
М(Х)=D(X)=10.
Геометрическое распределение
Проводим серию испытаний. В каждом из испытаний возможно наступление\ ненаступление события А. Причем вероятность наступления везде равна. Нас интересует вероятность того, что в серии из n испытаний наступит k успехов (наступление события). Нас интересует наступление события А.
Дискретная случайная величина Х обозначает число испытаний, предшествующих наступлению события А (Х=N).
Пусть в первых k-1 испытаниях событие А не наступило, а в k-м испытании появилось. Вероятность этого события по теореме умножения вероятностей независимых событий: P ( X = k ) = q k-1p.
Дискретная случайная величина имеет геометрическое распределение, если ее закон распределения имеет вид теоремы умножения вероятностей независимых событий. Дискретная величина, распределенная по этому закону имеет математическое ожидание и дисперсию вида:
МХ=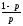
;DX=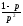
.
Пример 3. Игральная кость подбрасывается до первого появления цифры 5. Найти математическое ожидание и дисперсию для случайной величины X числа осуществляемых подбрасываний. p=1/6, q=5/6. В соответствии с имеющимися данными находим математическое ожидание и дисперсию по формулам: M(X)= 5
D(X)=30.