МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

УО «БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ»

Кафедра высшей математики

Лабораторная работа

по дисциплине: Теория вероятностей

на тему: Случайные величины

Студент

ФМк, 2-й курс, ДМП К.И. Машуков

Руководитель А.И. Астровский

МИНСК 2015

Основные теоретические сведения

Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.

Дискретной называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным. Непрерывной называют случайную величину, которая принимает значения, образующие интервал.

Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями. Закон распределения дискретной случайной величины можно задать таблично, в виде формулы (аналитически) и графически.

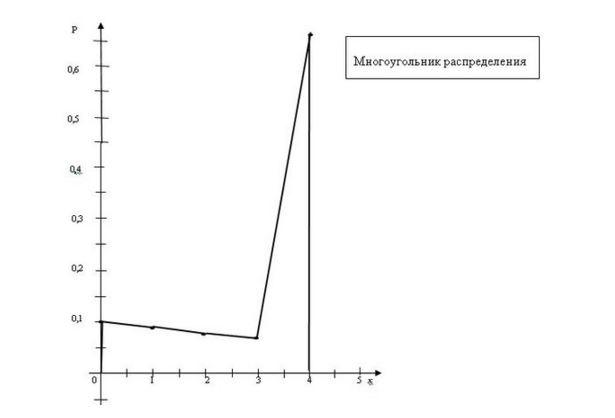
Чтобы отобразить его графически необходимо в прямоугольной системе координат построить ломаную, соединяющую последовательно точки с координатами (х_i; р_i), i=1,2, … ,n. Полученную линию называют многоугольником распределения.

Одной из важнейших характеристик случайной величины является математическое ожидание М(Х). Математическим ожиданием дискретной величины называют сумму произведений всех ее возможных значений на их вероятности: M(X)=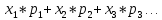,где x-возможные значения случайной величины X, а p- соответствующие вероятности. Вероятностный смысл математического ожидания заключается в том, что оно приближено равно среднему арифметическому наблюдаемых значений случайной величины.

Свойства математического ожидания:

1. Математическое ожидание постоянной величины равно самой постоянной: M(C)=C.

2. Постоянный множитель можно выносить за знак математического ожидания: М(CX)=C*M(X), C=const

3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий: M(XY)=M(X)*M(Y).

4. Математическое ожидание алгебраической суммы конечного числа случайных величин равно алгебраической сумме их математических ожиданий слагаемых: М(Х +Y)=М(Х)+М(Y).

Разность между случайной величиной и ее математическим ожиданием называется отклонением. При этом математическое ожидание отклонения равно нулю: M(X-M(X))=0. Это объясняется тем, что одни возможные отклонения положительны, другие отрицательны, и в результате их взаимного погашения получается ноль.

Еще одной характеристикой случайной величины является степень разброса значений случайной величины около ее математического ожидания – дисперсия D(X).

Дисперсия – это математическое ожидание квадрата отклонения случайной величины от математического ожидания, т.е. D(X)=М[(Х-М(Х))²].

Основные свойства дисперсии DX:

1. Дисперсия постоянной величины равна нулю, т.е. D(C)=0

2. Постоянный множитель можно выносить за знак дисперсии, возводя в квадрат, т.е. D(СX)=С² D(X).

3. Дисперсия суммы (разности) двух независимых случайны величин равна сумме дисперсий этих случайных величин: D(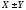)=D(X)+D(Y).

Среднеквадратическим отклонением случайной величины называется величина .

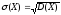Модой Мо(Х) непрерывной случайной величины Х называется значение Х, принимаемое с наибольшей вероятностью в сравнении с другими значениями, т.е. такое значение х случайной величины, при которой вероятность максимальна.

Медианой Ме(Х) случайной величины Х называют такое ее значение, для которой Р(Х<Me(X))=P(X>Me(X))=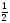. То есть плотность вероятностей справа и слева одинаковы и равны половине.

Квантилем уровня q (q-квантилем, х_q) называют решение уравнения F(x_q)=P(X<x_q)=q.